A block is released on the convex surface of a hemispherical wedge as shown in Fig. Determine the displacement of the wedge when the block reaches the angular position θ
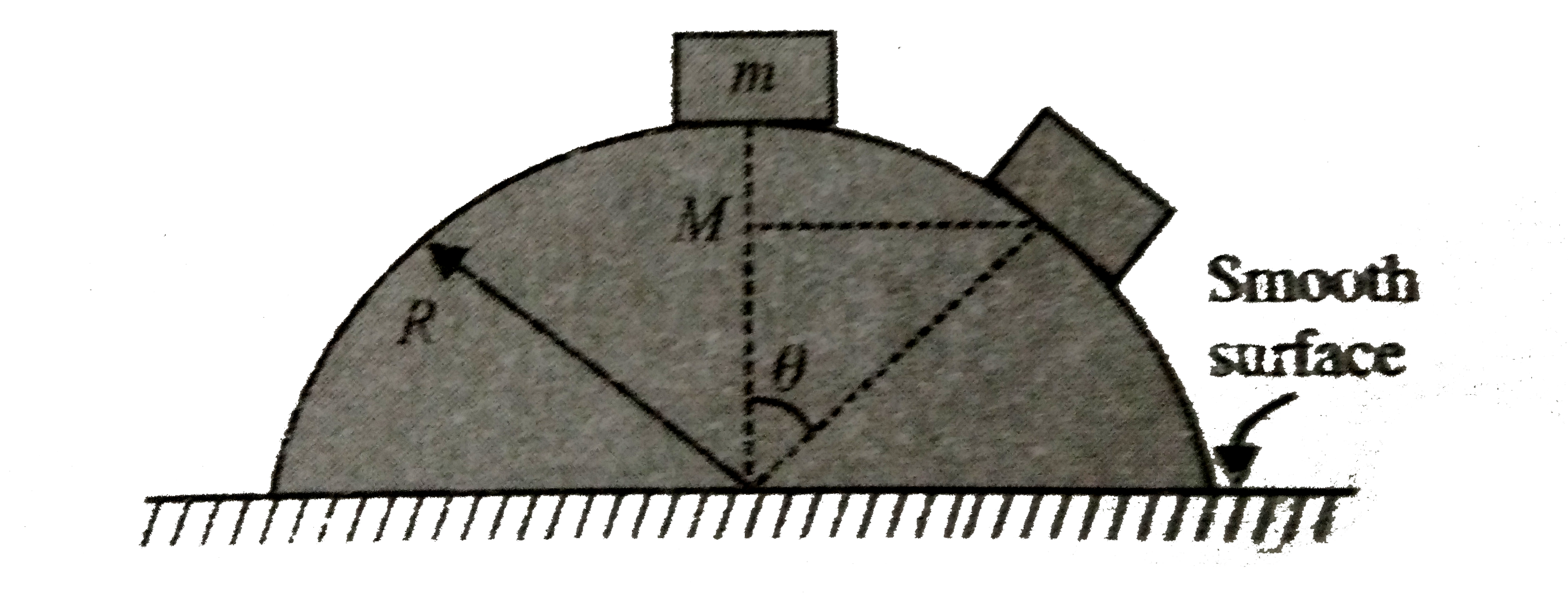
Applying work energy theorem

Wgravity=△K'+△KC…………..i
△K'= change in KE w.r.t centre of mass from and △KC= change in kinetic energy of centre of mass w.r.t ground.
Let v is the velocities of ball wilth respect to wedge and V is the velocity of wedge.
Linear mometum will be conserved in the horizontal direction . Hence MV=(vcosθ−V)
⇒V=mvcosθ(m+M) ...............ii
The velocity of centre of mas will be zero in horizontal direction but the velocity of centre of mass will change in vertical direction .
(vcm)y=mvsinθ(m+M) .............iii
Now applying WE theorem
−mgR(1−cosθ)=12μv2+12(m+M)v2cm,y
Here μ=mM(m+M) and vcm,y=mvsinθ(m+M)
which gives v=
⎷2(M+m)gR(1−cosθ)(M+Msin2θ)
and from eqn ii V=
⎷2m2gR(1−cosθ)cos2θ(M+m)(M+Msin2θ)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.1
20 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - Exercise 1.2
23 Videos
- CENTRE OF MASSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE
1 Videos
- CALORIMETRYBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CALORIMETRYEXERCISE - Solved Example
13 Videos
- DIMENSIONS & MEASUREMENTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer
2 Videos
Similar Questions
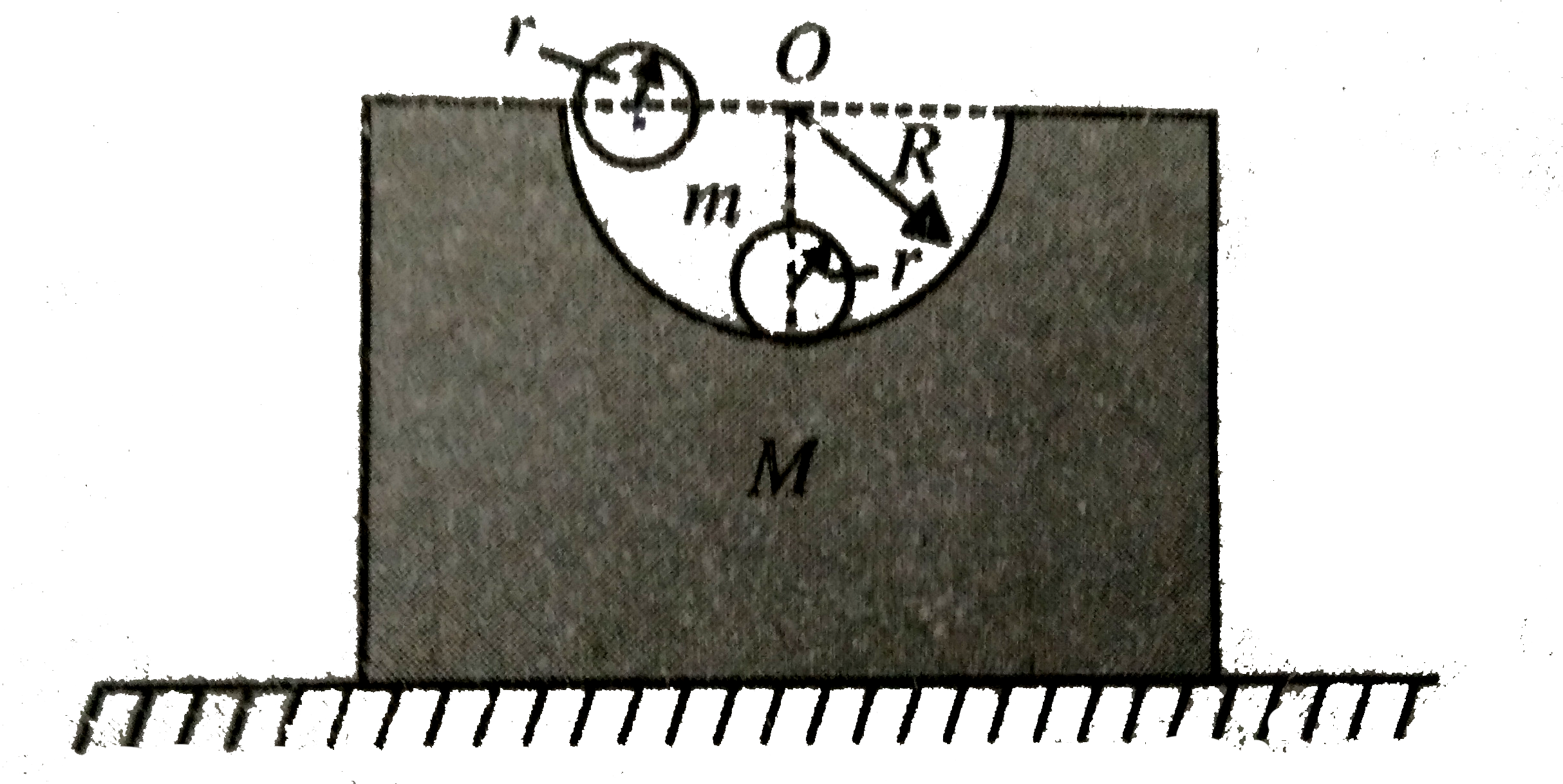
Calculate the displacement of the wedge when the hall reaches at the bottom of the groove,
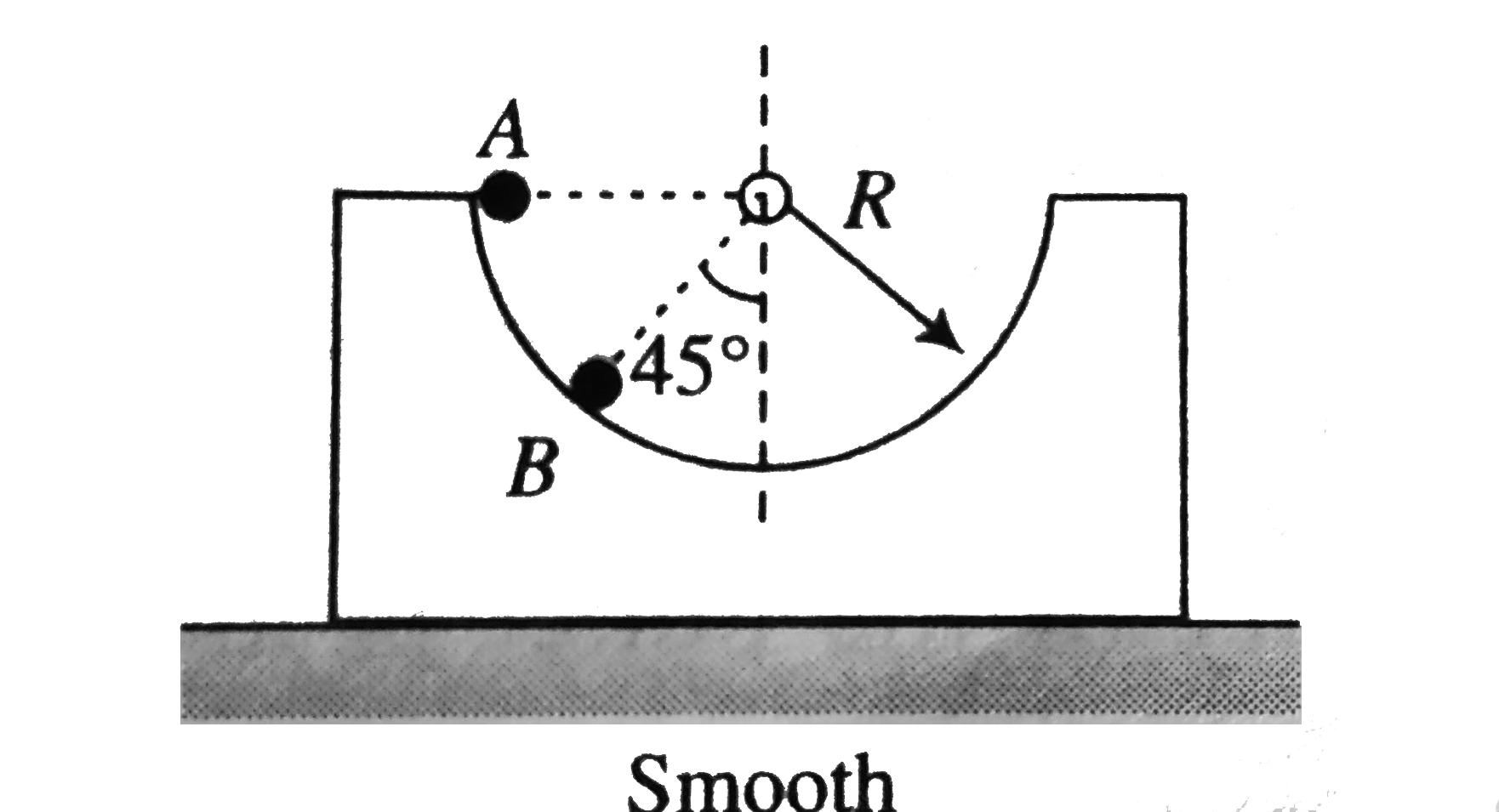
View SolutionA ball of mass m is released from A inside a smooth wedge of mass m as shown in figure. What is the speed of the wedge when the ball reaches point B?
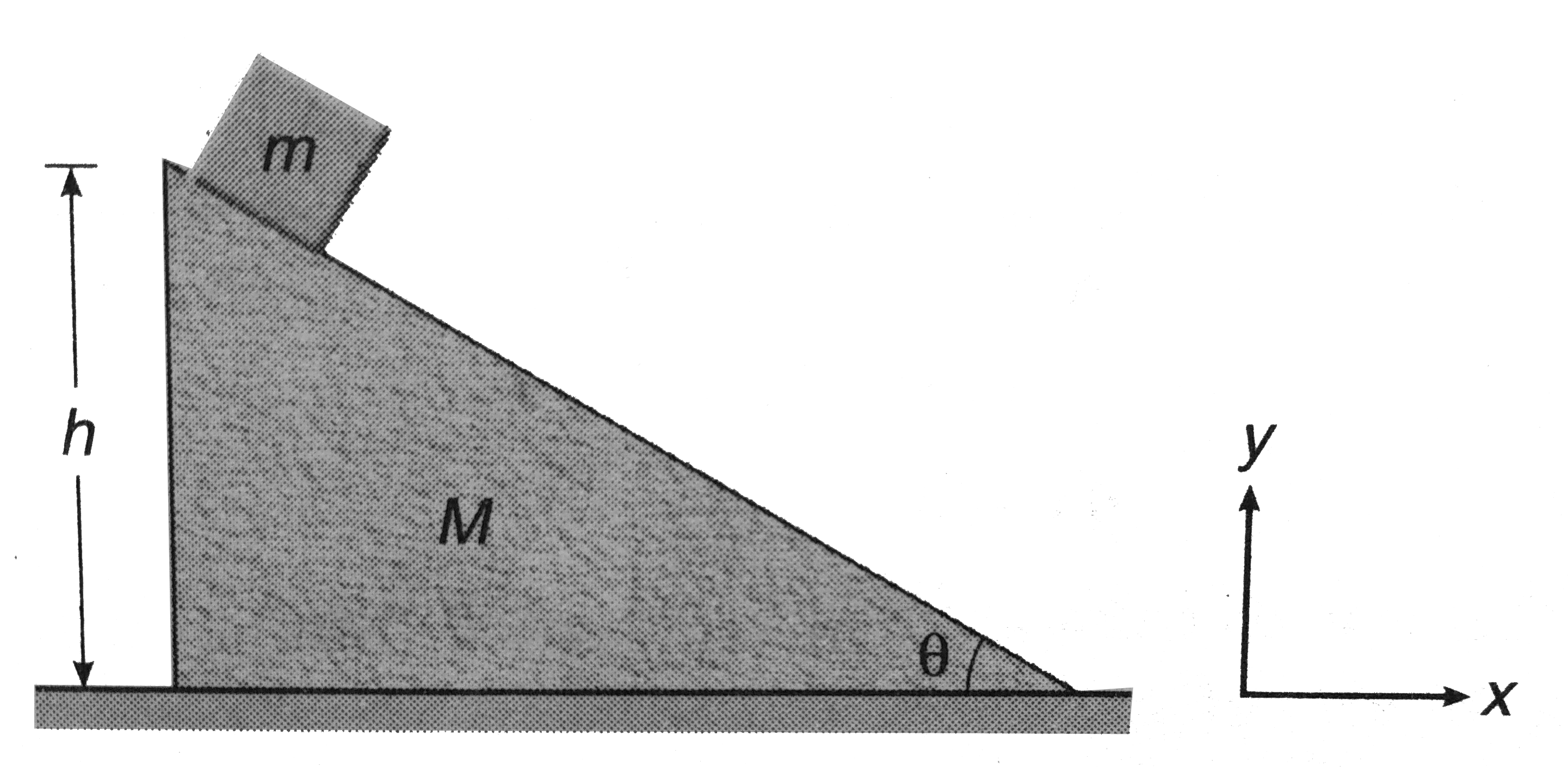
View SolutionA block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
View SolutionA block of mass m is placed on the inclined sufrace of a wedge as shown in fig. Calculate the acceleration of the wedge and the block when the block is released. Assume all surfaces are frictionless.

View SolutionA block of mass m is at rest on a rough wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionA block of mass m is at rest on a rought wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionA block of mass m is at rest on a rough wedge as shown in figure. What is the force exerted by the wedge on the block?

View SolutionAll surfaces shown in figure are smooth. Find velocity of wedge (of mass M) when the block (of mass m) reaches the bottom of the wedge.

View SolutionA small block of mass m is placed at rest on the top of a smooth wedge of mass M, which in turn is placed at rest on a smooth horizontal surface as shown in figure. If h be the height of wedge and θ is the inclination, then the distance moved by the wedge as the block reaches the foot of the wedge is
View SolutionA block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
View Solution
