The magnetic field existing in a region is given by →B=B0(1+xl)→k. A square loop of edge l and carrying a current I, is placed with its edges parallel to the x-y axes. Find the magnitude of the net magnetic force experienced by the loop.
To find the magnitude of the net magnetic force experienced by a square loop carrying a current in a magnetic field, we can follow these steps:
Step 1: Understand the Magnetic Field and Loop Configuration
The magnetic field is given by:
→B=B0(1+xl)^k
This indicates that the magnetic field is in the z-direction and varies with the x-coordinate.
The square loop has an edge length l and is placed in the x-y plane, with its edges parallel to the x and y axes.
Step 2: Identify the Sides of the Loop
Label the corners of the square loop as:
- A (0, 0)
- B (l, 0)
- C (l, l)
- D (0, l)
The sides of the loop are:
- AB (from A to B)
- BC (from B to C)
- CD (from C to D)
- DA (from D to A)
Step 3: Calculate the Force on Each Side
The magnetic force on a current-carrying wire is given by:
→F=I→L×→B
where →L is the length vector of the wire segment.
Force on Side AB
For side AB, x=0:
→B=B0(1+0l)^k=B0^k
The length vector →LAB=l^i.
Thus, the force →FAB is:
→FAB=Il^i×B0^k=IlB0^j
Force on Side BC
For side BC, x=l:
→B=B0(1+ll)^k=2B0^k
The length vector →LBC=l^j.
Thus, the force →FBC is:
→FBC=Il^j×2B0^k=−2IlB0^i
Force on Side CD
For side CD, x=l:
→B=2B0^k
The length vector →LCD=−l^i.
Thus, the force →FCD is:
→FCD=−Il^i×2B0^k=−2IlB0^j
Force on Side DA
For side DA, x=0:
→B=B0^k
The length vector →LDA=−l^j.
Thus, the force →FDA is:
→FDA=−Il^j×B0^k=IlB0^i
Step 4: Sum the Forces
Now, we can sum the forces:
- →FAB=IlB0^j
- →FBC=−2IlB0^i
- →FCD=−2IlB0^j
- →FDA=IlB0^i
Combining these:
→Fnet=(IlB0^j−2IlB0^i−2IlB0^j+IlB0^i)
=(−IlB0^i−IlB0^j)
Step 5: Calculate the Magnitude of the Net Force
The magnitude of the net force is:
|→Fnet|=√(−IlB0)2+(−IlB0)2=√2(IlB0)2=IlB0√2
Final Answer
The magnitude of the net magnetic force experienced by the loop is:
|→Fnet|=IlB0√2
The magnetic field is given by:
→B=B0(1+xl)^k
This indicates that the magnetic field is in the z-direction and varies with the x-coordinate.
Label the corners of the square loop as:
- A (0, 0)
- B (l, 0)
- C (l, l)
- D (0, l)
- AB (from A to B)
- BC (from B to C)
- CD (from C to D)
- DA (from D to A)
The magnetic force on a current-carrying wire is given by:
→F=I→L×→B
where →L is the length vector of the wire segment.
For side AB, x=0:
→B=B0(1+0l)^k=B0^k
The length vector →LAB=l^i.
Thus, the force →FAB is:
→FAB=Il^i×B0^k=IlB0^j
For side BC, x=l:
→B=B0(1+ll)^k=2B0^k
The length vector →LBC=l^j.
Thus, the force →FBC is:
→FBC=Il^j×2B0^k=−2IlB0^i
For side CD, x=l:
→B=2B0^k
The length vector →LCD=−l^i.
Thus, the force →FCD is:
→FCD=−Il^i×2B0^k=−2IlB0^j
For side DA, x=0:
→B=B0^k
The length vector →LDA=−l^j.
Thus, the force →FDA is:
→FDA=−Il^j×B0^k=IlB0^i
Now, we can sum the forces:
- →FAB=IlB0^j
- →FBC=−2IlB0^i
- →FCD=−2IlB0^j
- →FDA=IlB0^i
→Fnet=(IlB0^j−2IlB0^i−2IlB0^j+IlB0^i)
=(−IlB0^i−IlB0^j)
The magnitude of the net force is:
|→Fnet|=√(−IlB0)2+(−IlB0)2=√2(IlB0)2=IlB0√2
The magnitude of the net magnetic force experienced by the loop is:
|→Fnet|=IlB0√2
Topper's Solved these Questions
Similar Questions
The magnetic field existing in a region is given by B=B0(1−xy)ˆk, where B0 and l ae constant x is the x coordinate of a point and ˆk is the unit vector along Z axis.A square loop of edge and carrying a current is placed with his edges parallel to the x,y axes.Find the magnitude of the net magnetic force experienced by the loop.
View SolutionThe magnetic field in a region is given by →B=B0(xa)ˆk. A square loop of side d is placed with its edges along the x and y axes. The loop is moved with a constant velocity →v=v0ˆi The emf induced in the loop is :

View Solution
Knowledge Check
The magnetic field in a region is given by →B=B0(1+xa)ˆk. A square loop of edge length 'd' is placed with its edge along X-axis and Y-axis. The loop is moved with a constant velocity →V=V0ˆi. The emf induced in the loop is
Av0B0d2aBv0B0d3aCv0B0d22aD0A square loop of edge 'a' carries a current l. The magnetic field at the centre of loop is
Aμ0l2√2πaB2√2μ0lπaCμ0l√2πaDμ0l√2πaWhen a conductor of length l carrying a current I is placed in a magnetic field of induction B at an angle θ with respect to →B, the force experienced by it is
AF=IBlBF=IBlsinθCF=IBlcosθDF=IBltanθ
A hypthetical magnetic field existing in a region is given by →B=B0→er, where →–––r denotes the uit vector along the redial direction. A circular loop of radus a, carrying a current I, is placed with its plane parallel to the x-y plane and the centre at (0,0, d) .Find the magnitude of the magnetic force acting on the loop.
View SolutionThe magnetic field in a region is given by B=B0(1+xa)ˆk.A square loop of edge-length d is placed with its edges along the x and y-axes. The loop is moved with a constant velocity v=v0ˆi.The emf induced in the loop is:
View SolutionA square loop OABCO of side of side l carries a current i. It is placed as shown in figure. Find the magnetic moment of loop.
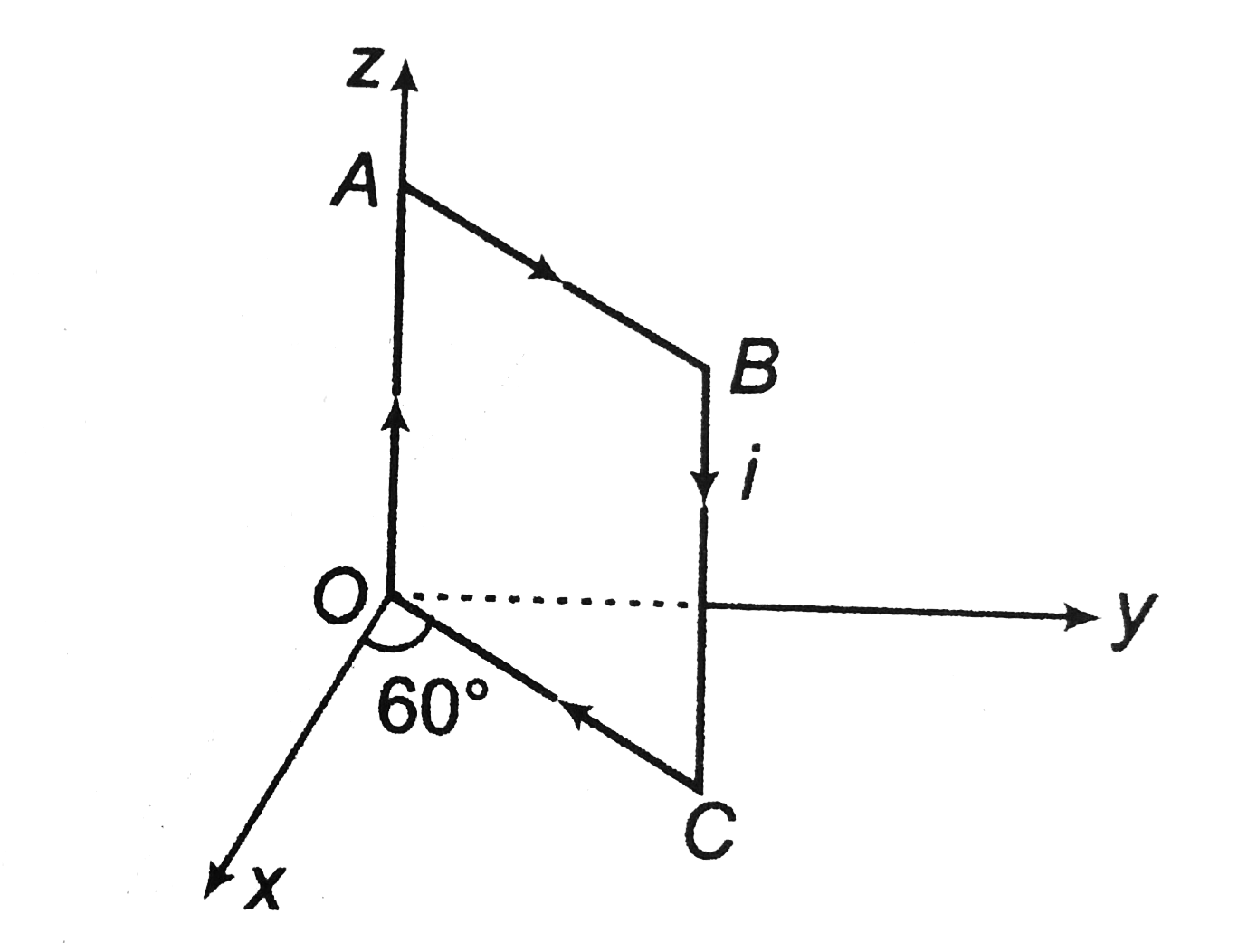
View SolutionA square loop of side l carries a current i. it is placed as shown in figure. Find the magnetic moment of the loop.
View SolutionThe magnetic field in a region is given by B=B0(1−XL)K. A straight conductor AB of length 2L, placed with its ends at points A (a,0,0) and B(a,2L,0), carries a current I from A to B. Find the magnetic force on the conductor
View Solution

