The magnetic field in a region is given by B=B0(1−XL)K. A straight conductor AB of length 2L, placed with its ends at points A (a,0,0) and B(a,2L,0), carries a current I from A to B. Find the magnetic force on the conductor
The correct Answer is:2IB0(L−a)ˆi
To find the magnetic force on the conductor AB, we will follow these steps:
Step 1: Understand the Magnetic Field
The magnetic field is given by:
B=B0(1−XL)^k
This indicates that the magnetic field varies with the x-coordinate and is directed along the z-axis (k-direction).
Step 2: Identify the Coordinates of Points A and B
The coordinates of the points are:
- Point A: (a,0,0)
- Point B: (a,2L,0)
The length of the conductor AB is 2L and it is oriented along the y-axis.
Step 3: Calculate the Magnetic Field at Point A
Since the magnetic field varies with the x-coordinate, we need to evaluate it at point A where X=a:
B(a)=B0(1−aL)^k
Step 4: Define the Length Vector of the Conductor
The conductor AB has a length vector L which is directed along the y-axis:
L=2L^j
Step 5: Use the Formula for Magnetic Force
The magnetic force F on a current-carrying conductor is given by:
F=IL×B
Substituting the values we have:
F=I(2L^j)×(B0(1−aL)^k)
Step 6: Calculate the Cross Product
To compute the cross product ^j×^k:
^j×^k=^i
Thus, we can simplify the force:
F=I(2L)B0(1−aL)^i
Step 7: Final Expression for the Magnetic Force
The final expression for the magnetic force on the conductor is:
F=2IB0(1−aL)L^i
Summary
The magnetic force on the conductor AB is directed along the x-axis and is given by:
F=2IB0(1−aL)L^i
The magnetic field is given by:
B=B0(1−XL)^k
This indicates that the magnetic field varies with the x-coordinate and is directed along the z-axis (k-direction).
The coordinates of the points are:
- Point A: (a,0,0)
- Point B: (a,2L,0)
Since the magnetic field varies with the x-coordinate, we need to evaluate it at point A where X=a:
B(a)=B0(1−aL)^k
The conductor AB has a length vector L which is directed along the y-axis:
L=2L^j
The magnetic force F on a current-carrying conductor is given by:
F=IL×B
Substituting the values we have:
F=I(2L^j)×(B0(1−aL)^k)
To compute the cross product ^j×^k:
^j×^k=^i
Thus, we can simplify the force:
F=I(2L)B0(1−aL)^i
The final expression for the magnetic force on the conductor is:
F=2IB0(1−aL)L^i
The magnetic force on the conductor AB is directed along the x-axis and is given by:
F=2IB0(1−aL)L^i
Topper's Solved these Questions
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Assignment Problems (Subjective) (Level - II & III)
Explore 15 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Assignment Problems (Objective) (LEVEL-I)
Explore 50 Videos
- MAGNETICBook:FIITJEEChapter:MAGNETICExercise:Exercise
Explore 11 Videos
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
- MAGNETISMBook:FIITJEEChapter:MAGNETISMExercise:Example
Explore 12 Videos
Similar Questions
The magnetic field existing in a region is given by →B=B0(1+xl)→k. A square loop of edge l and carrying a current I, is placed with its edges parallel to the x-y axes. Find the magnitude of the net magnetic force experienced by the loop.
View SolutionThe magnetic field in a region is given by →B=B0Lxˆk where L is a fixed length.A conducting rod of length lies along the X-axis between the origin and the point (L,0,0).If the rod moves with a velocity →v=v0ˆj the emf induced between the ends of the rod.
View Solution
Knowledge Check
A conductor has three segments, two straights of length L and a semicircular with radius R. It carries a current I What is the magnetic field B at point P?
 Aμ0I4πRBμ04πIR2Cμ0I4RDμ0I4π
Aμ0I4πRBμ04πIR2Cμ0I4RDμ0I4π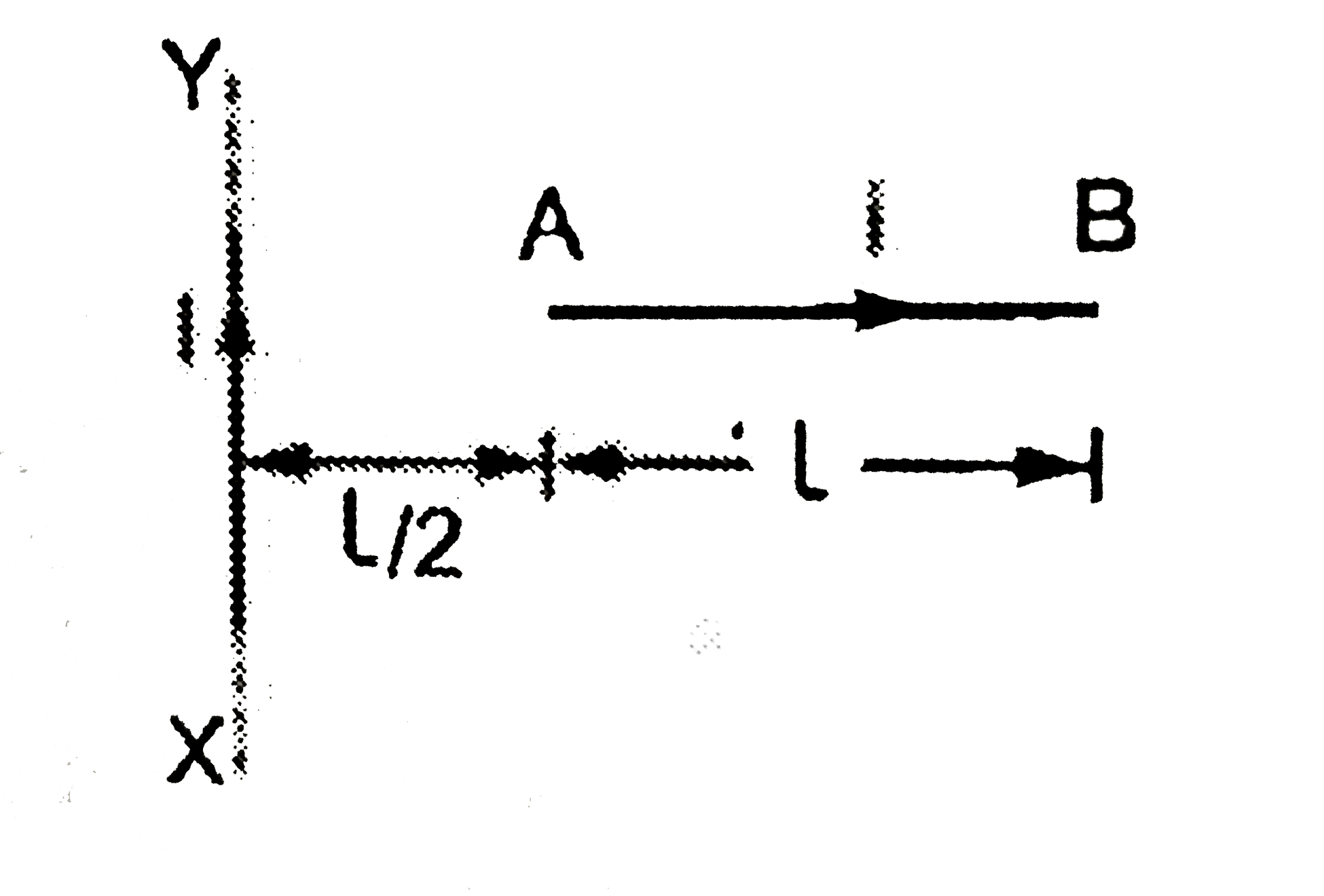
A conductor AB of length l carrying a current i is placed perpendicular to a long straight conductor XY carrying a current I, as shown. The force on AB will actAupwardBdownwardCto the rightDto the leftA conductor AB of length L carrying a current I', is placed perpendicular to a long straight conductor XY carrying a current I as shown in Fig. The forces on AB has magnitude
 Aμ0I'I2πlog2Bμ0I'I2πlog3C3μ0I'I2πlog32D2μ0I'I3π
Aμ0I'I2πlog2Bμ0I'I2πlog3C3μ0I'I2πlog32D2μ0I'I3π
The magnetic field inn a region is given by →B=→kB0LywhereLisafixed≤n>h.Aconduct∈grodof≤n>hLliesalongtheY−aξsbetweentheorig∈andthep∮(0,L,0).Iftherodmoveswithavelocityv= v_0 veci, find the emf induced between the ends of the rod.
View SolutionA conductor of length 1m and carrying current of 1A is placed parallel to the magnetic field of 1gauss.The magnetic force acting on the conductor is: ?
View SolutionA straight conductor of length ro carrying a current l is placed perpendicular to a long straight conductor which carries a current io as shown in the figure. Find the force of interaction between them.

View SolutionA current i is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be-
View SolutionA conductor AB of length l carrying current i is placed perpendicular to a long straight conductor carrying a current I as shown. Force on AB will be

View Solution

