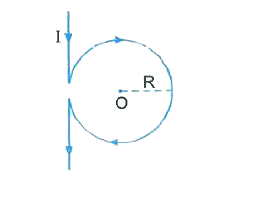
A current I flows in a long straight wire (into the plane of the paper) with cross-section having the from of a circular are of radius R a shown in the figure. Find the magnetic induction at the point O.
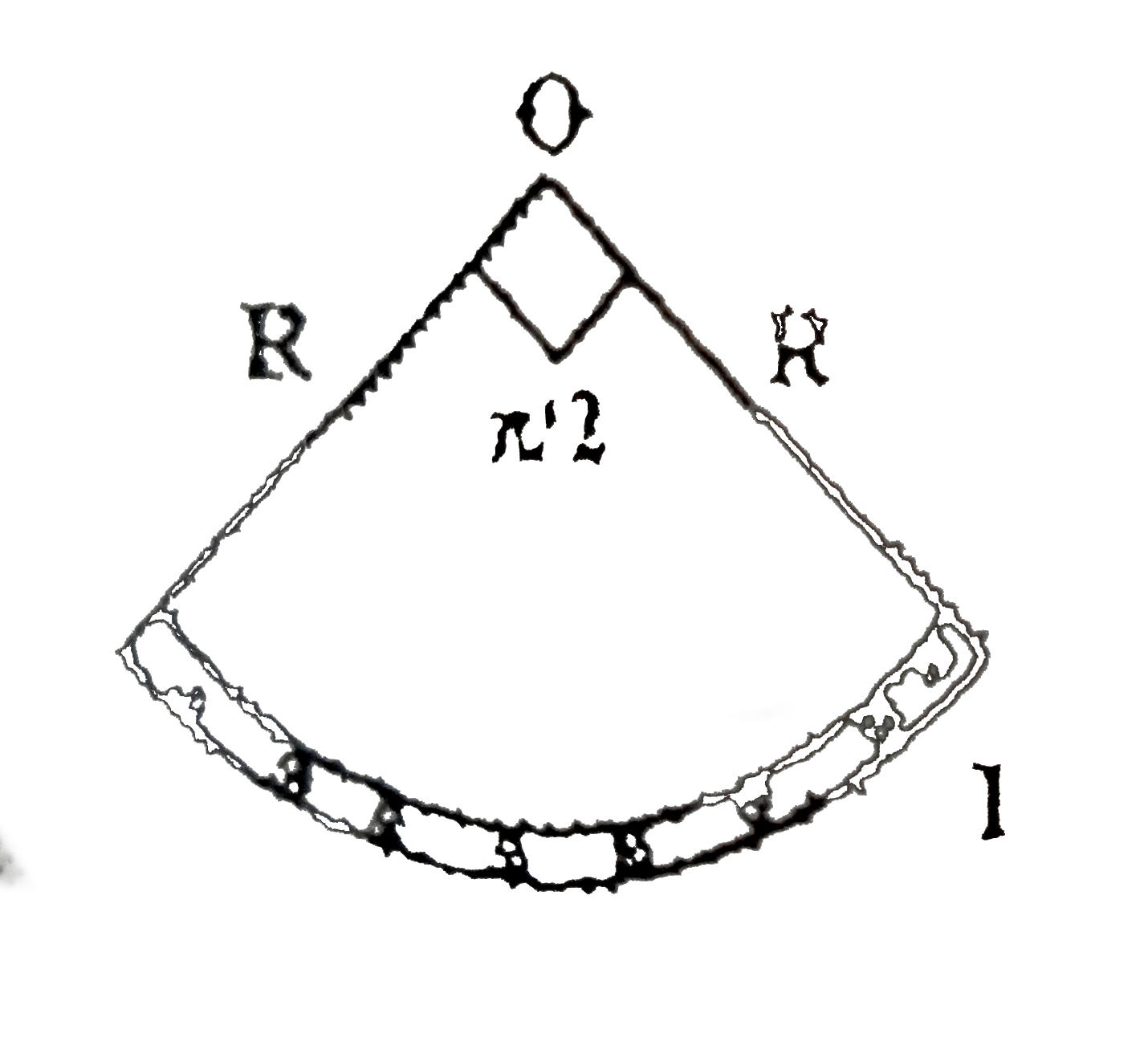
We have the result of magnetic filed for a straight conductor. For a distribution, we have to make a differential equation and integrate.
Consider a small element of width Rdθ as shown in the figure.
dB=μ0(dI)2πR
dI=IπR2dθ=2Iπdθ∴dB=μ0Idθπ2R
As we have to integrate x and y components separately.
dBx=dBcosθ=μ0Iπ2Rcosθdθ
dBy=dBsinθ=μ0Iπ2Rsinθdθ
Bx=∫dBx=μ0Iπ2R∫+π/4−π/4cosθdθ=μ0I√2π2R
By=∫dBy=μ0Iπ2R∫+π/4−π/4sinθdθ=0
→B=μ0I√2π2Rˆi
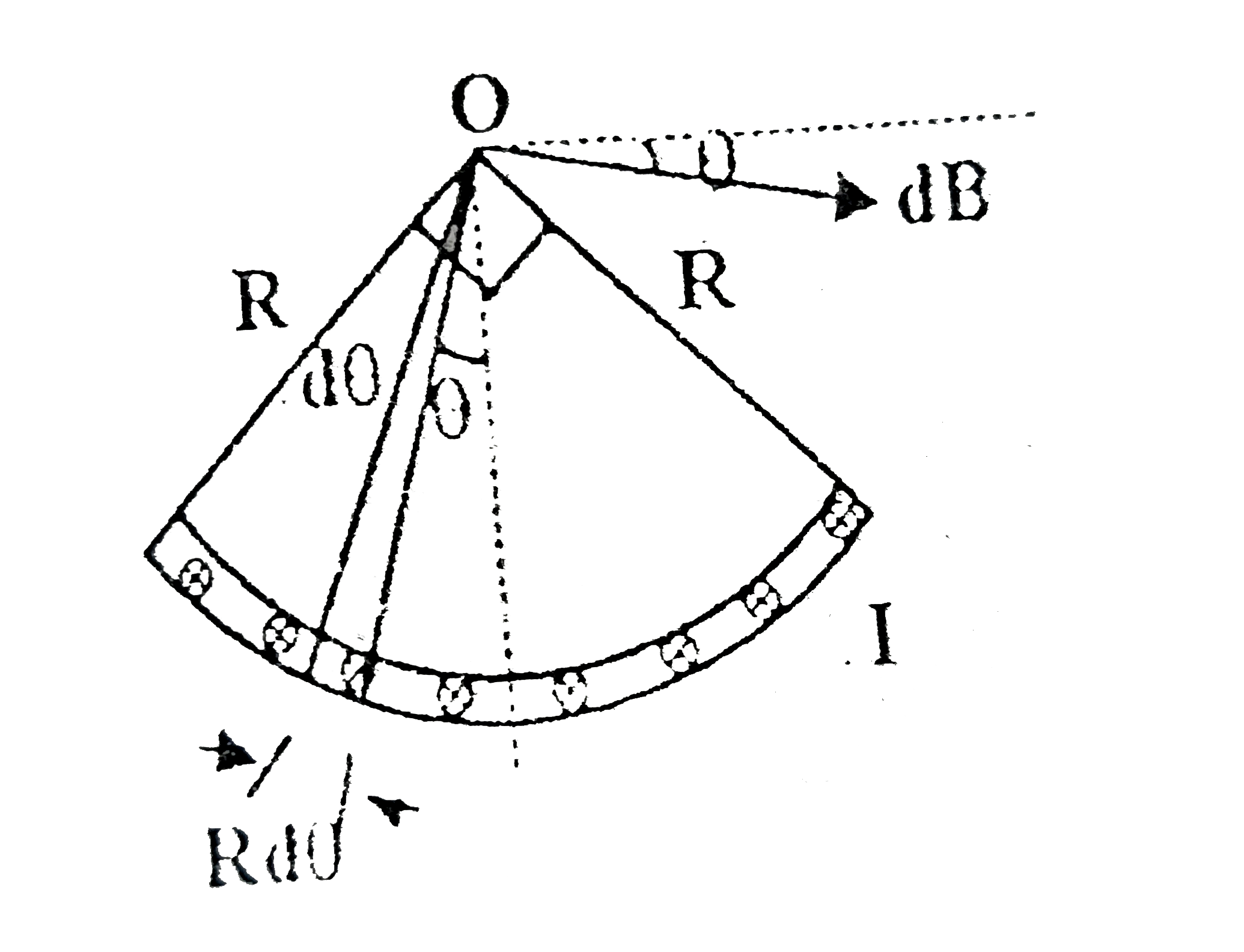
Topper's Solved these Questions
Similar Questions
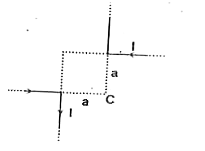
Two inflinitely long wires carrying current I, are bent as shown in the figure. Find the magnetic induction at point C.
View SolutionA current I flows in a long straight wire with cross-section haviing the form of a thin half-ring of radius R (Fig). Find the induction of the magnitude field at the point O.

View Solution
Knowledge Check
A current I flows an infinitely long wire with cross section in the form of a semi - circular ring of radius R. The magnitude of the magnetic induction along its axis is :
Aμ0I2π2RBμ0I2πRCμ0I4πRDμ0Iπ2RA current I flows through a long straight conductor which is bent into a circular loop of radius R in the middle as shown in the figure .
The magnitude of the net magnetic field at point O will beAZeroBμ0I2R(1+π)Cμ0I4πRDμ0I2R(1−1π)A current I, flowing in a long and straight wire along z-axis, is directed into two identical semicircular portions lying in y-z and x-z planes as shown in the figure. The magnetic field at the centre O is
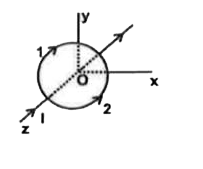 AzeroBμ0l4πCμ0l2√2rDμ0l√2r
AzeroBμ0l4πCμ0l2√2rDμ0l√2r
A current I flows in a long straight wire whose cross section is in the shape of a thin quarter ring of radius R. Find the induction of the magnetic field (B) at point O on the axis.

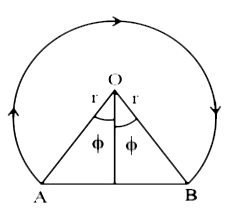
View SolutionA wire is bent in the form of a circular arc of radius r with a straight portion AB. If the current in the wire is i, then the magnetic induction at point O is
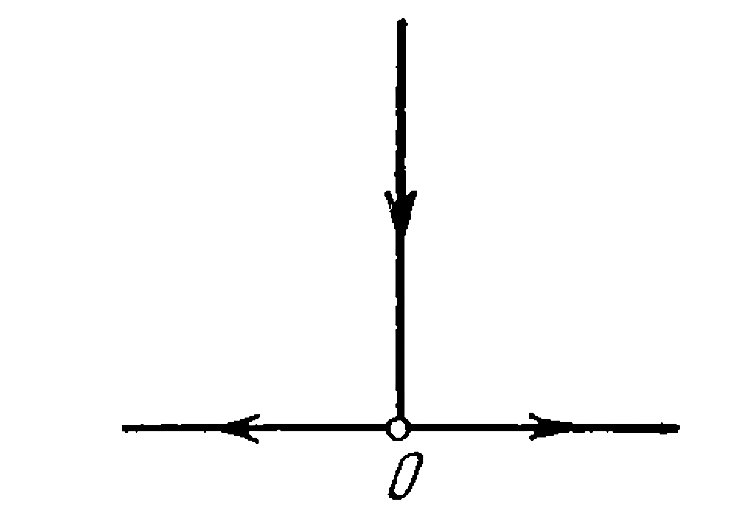
View SolutionA direct current I flows along a lengthly straight wire. From the point O (fig) the current sperads radially all over an infinite conducting plane paerpendicular to the wire. Find the magnatic induction at all points of space.
View SolutionA direct current I flows in a long straight conductor whose cross section has the form of a thin halr-ring of radius R. The same current flows in the opposite direction along a thin conductor located on the axis of the first conductor. Find the magnetic induction froce between the given conductors reduced to a unit of their length.

View Solutionfigure 4.22 shows two long wires A and B, each carrying a current I, separated by a distance l and oriented in a plane perpendicular to the plane of paper. The directions of currents are shown in figure. Find the magnetic induction at a point P located at a distance l from both wires as shown in figure4.22
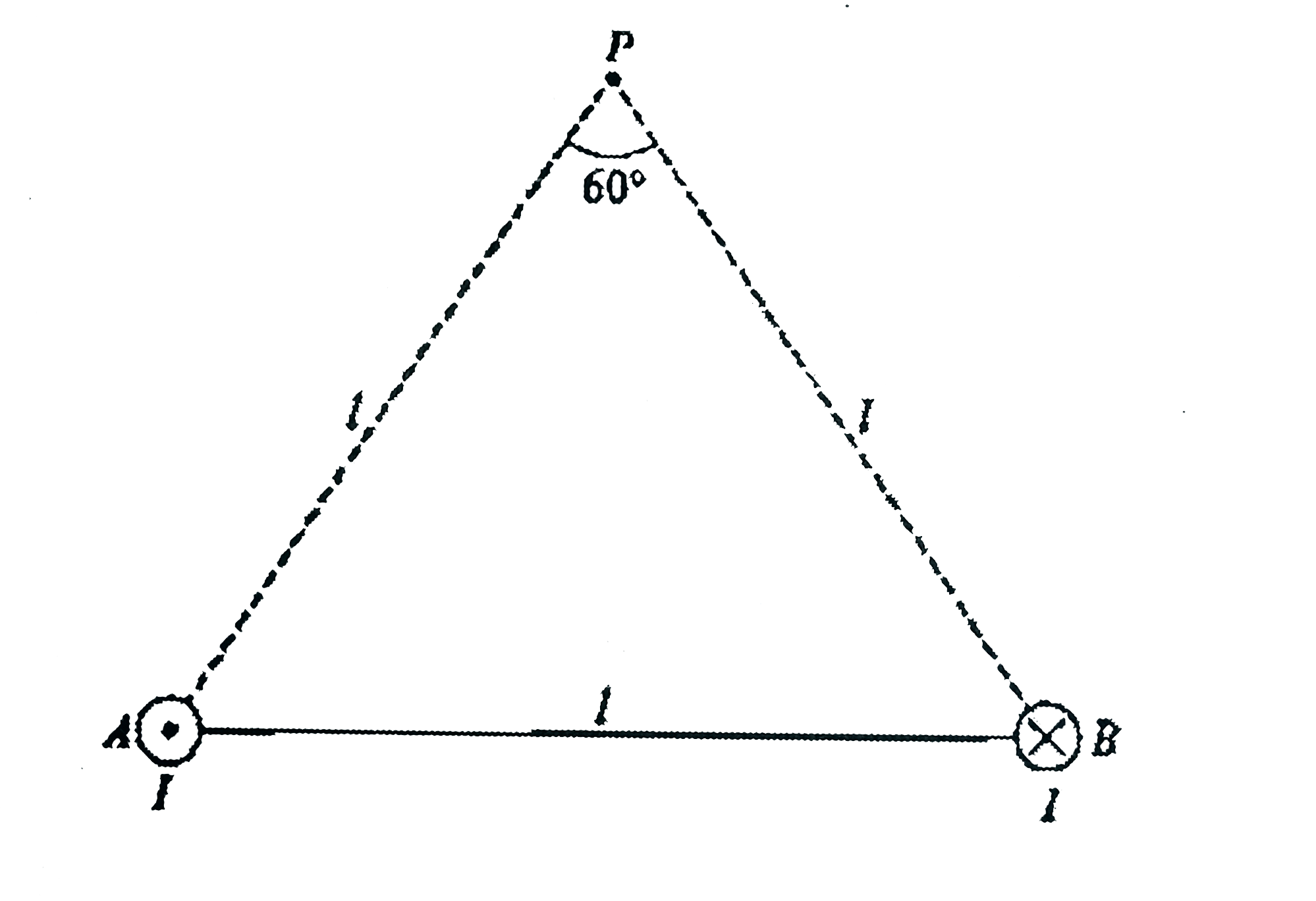
View Solution

