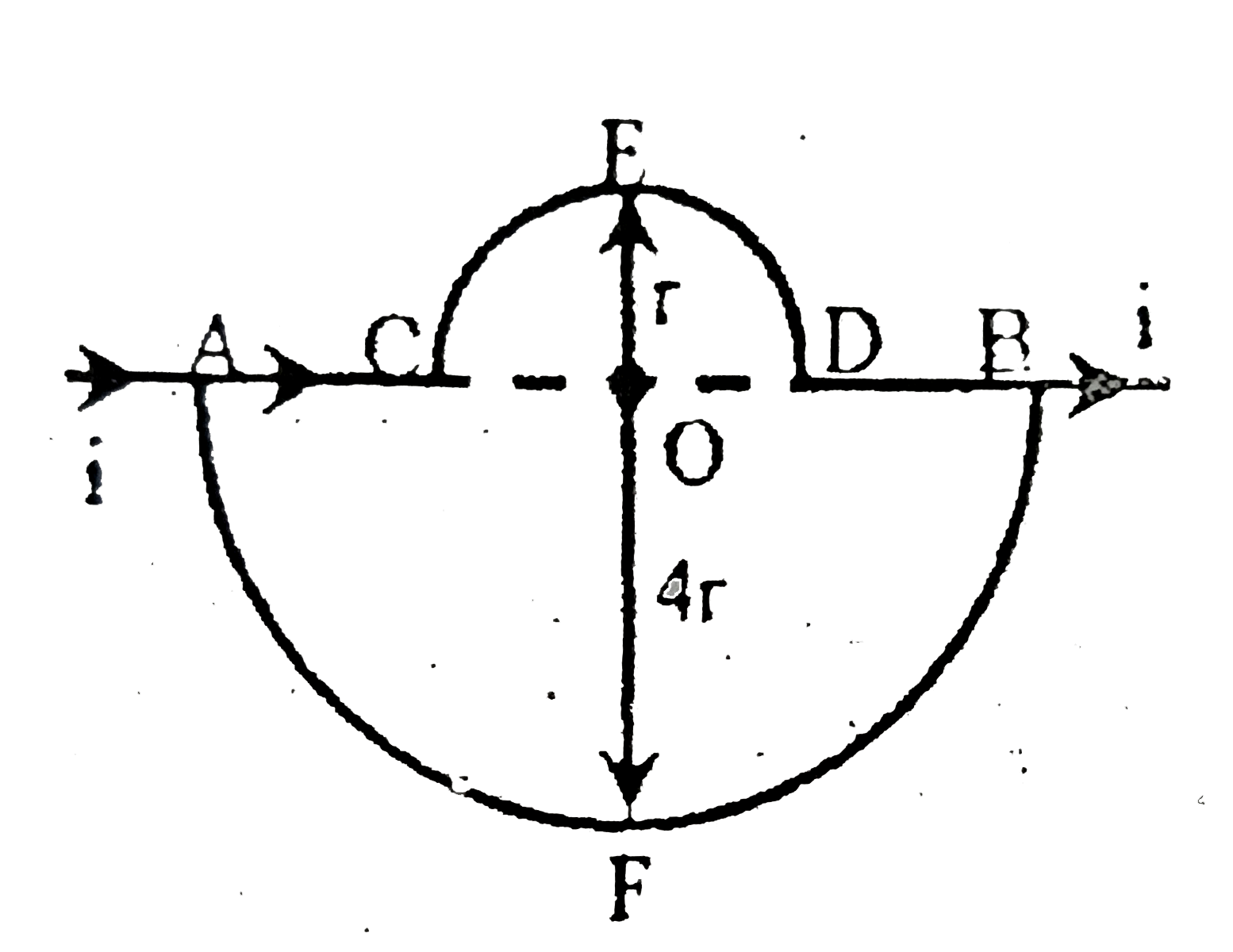
In the shown in the figure AC and BD are straight lines and CED and AFB are semicircular with radii r and 4r, respectively. The centre setip is lying in the same plane. If i is current entering at A what fraction of i will flow in the ACEDB such that resultant magnetic field at O is zero.
I/5
4I/5
3I/5
no current through bigger semicircular part.
If I1 is current in ACDB then
μ04⋅i1r=μ04⋅i24r⇒i1i2=14
i1=15×i=i5
Topper's Solved these Questions
Similar Questions
Knowledge Check
A conductor has three segments, two straights of length L and a semicircular with radius R. It carries a current I What is the magnetic field B at point P?
 Aμ0I4πRBμ04πIR2Cμ0I4RDμ0I4π
Aμ0I4πRBμ04πIR2Cμ0I4RDμ0I4πTwo long straight wires are connected by a circular section which has a radius R. All the three segments lie in the same plane and carry a current I. The magnetic induction at the centre O of the circular segments is
 Aμ0I4πRBαμ0I4πRCαμ0IRDαμ0I2πR
Aμ0I4πRBαμ0I4πRCαμ0IRDαμ0I2πRA wire bent in the form of a sector of radius r subtending an angle θ∘ at centre as shown in figure is carrying a current I. The magnetic field at O is :
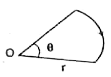 Aμ0I2rθBμ0I2r(θ/180)Cμ0I2r(θ/360)Dzero
Aμ0I2rθBμ0I2r(θ/180)Cμ0I2r(θ/360)Dzero
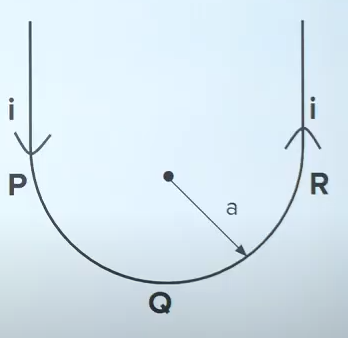
In figure shown U-shaped wire a current i is flowing as shown. Section PQR is a semicircle of radius a.If O is origin then find magnetic field at O
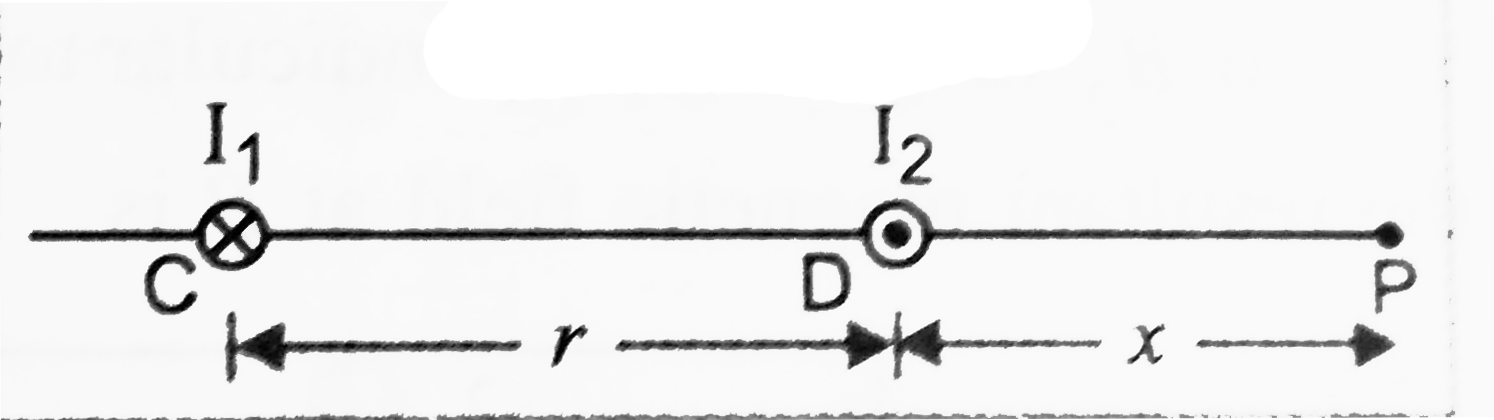
View SolutionTwo parallel wires C and D placed perpendicular to the plane of paper at a separation of r(=8cm), carry electric currents I1=6A and I2=3A in opposite directions as shown in figure. Find the point on the line CD where the resultant magnetic field is zero.
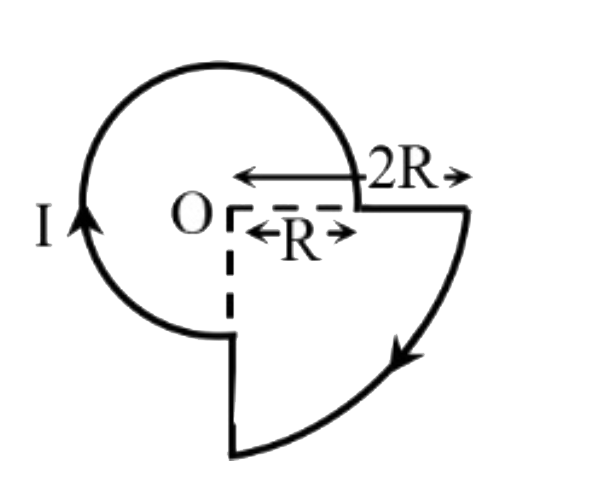
View SolutionA long wire carrying current 'I' is bent into the shape as shown in the figure. The net magnetic field intensity at the centre 'O' is

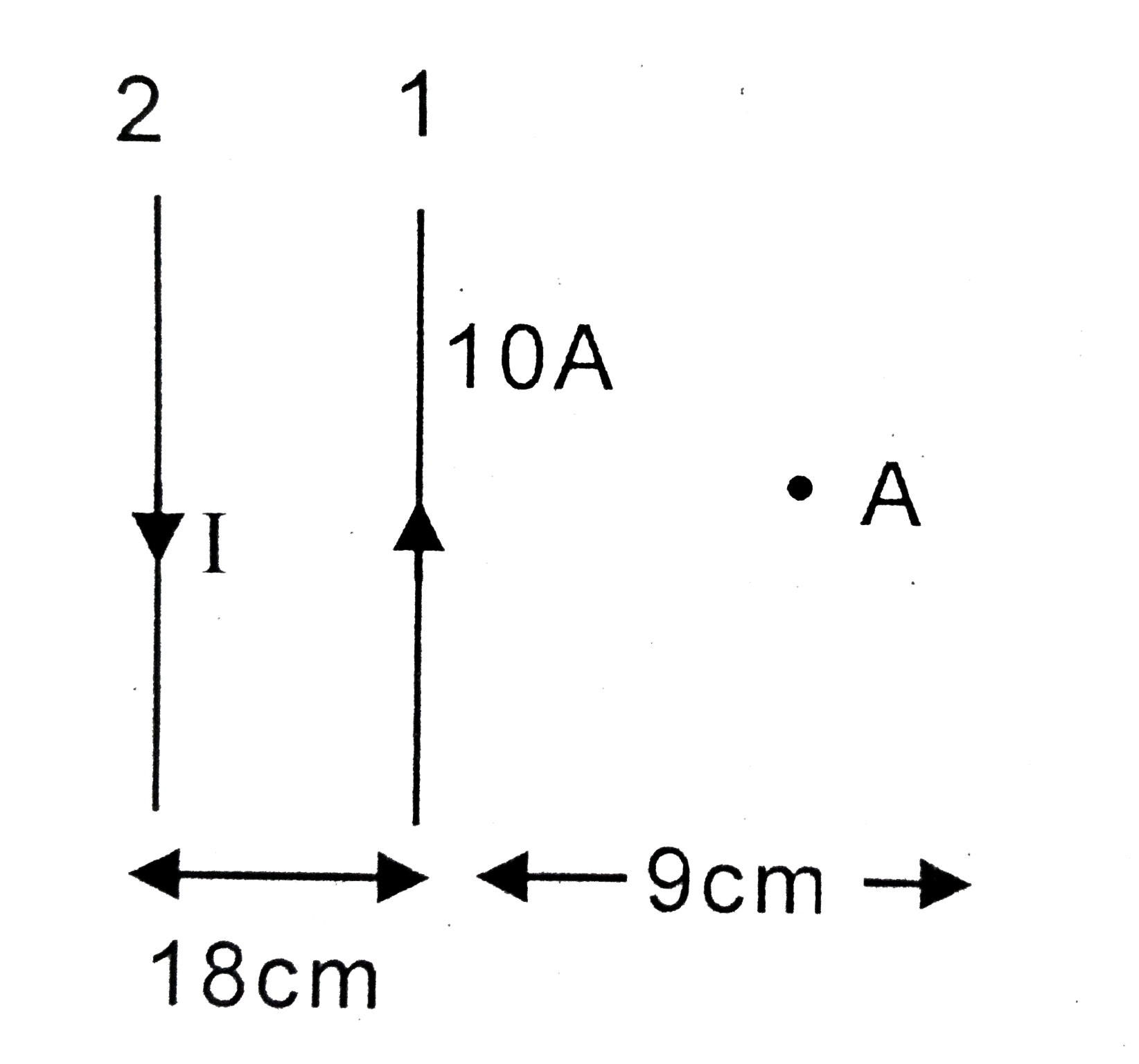
View SolutionIn figure two infinitely long current carrying wires are shown . If resultant magnetic field at point A is zero. Then determine current I1 .
View SolutionIn the figure shown there are two semicircles of radii r1 and r2 in which a current i is flowing. The magnetic induction at the centre O will be

View Solution