The magnetic field in a region is given by B=B0(1+xa)ˆk.A square loop of edge-length d is placed with its edges along the x and y-axes. The loop is moved with a constant velocity v=v0ˆi.The emf induced in the loop is:
zero
v0B0d
v0B0d3a2
v0B0d2a
To find the induced EMF in the square loop due to the changing magnetic field as it moves, we can follow these steps:
Step 1: Understand the Magnetic Field
The magnetic field is given by:
B = B_0 \left(1 + \frac{x}{a}\right} \hat{k}
This means the magnetic field varies with the position x of the loop.
Step 2: Identify the Loop's Position
The square loop has an edge length d and is placed with its edges along the x and y axes. As it moves with a constant velocity →v=v0^i, the position of the loop changes over time.
Step 3: Calculate the Magnetic Field at Different Positions
As the loop moves, the magnetic field at the left edge (at x) and the right edge (at x+d) of the loop will be different:
- At the left edge (position x):
Bleft=B0(1+xa)
- At the right edge (position x+d):
Bright=B0(1+x+da)
Step 4: Calculate the EMF Induced
The induced EMF E in the loop can be calculated using Faraday's law of electromagnetic induction, which states that the induced EMF is equal to the negative rate of change of magnetic flux through the loop.
The magnetic flux Φ through the loop is given by:
Φ=B⋅A
where A is the area of the loop. The area A of the square loop is:
A=d2
The change in magnetic flux as the loop moves can be expressed as:
E=−dΦdt
Step 5: Calculate the Change in Flux
The change in flux can be calculated as:
Φright−Φleft=(Bright−Bleft)⋅d2
Substituting the expressions for Bright and Bleft:
Φright−Φleft=(B0(1+x+da)−B0(1+xa))d2
This simplifies to:
Φright−Φleft=B0(da)d2
Step 6: Calculate the Induced EMF
Now, we can find the induced EMF:
E=−dΦdt=−B0(da)d2dt
Since the loop is moving with velocity v0, we can relate the change in time to the distance traveled:
E=−B0(da)d2⋅1v0
Final Expression
Thus, the induced EMF in the loop is:
E=B0d2v0a
The magnetic field is given by:
B = B_0 \left(1 + \frac{x}{a}\right} \hat{k}
This means the magnetic field varies with the position x of the loop.
The square loop has an edge length d and is placed with its edges along the x and y axes. As it moves with a constant velocity →v=v0^i, the position of the loop changes over time.
As the loop moves, the magnetic field at the left edge (at x) and the right edge (at x+d) of the loop will be different:
- At the left edge (position x):
Bleft=B0(1+xa)
- At the right edge (position x+d):
Bright=B0(1+x+da)
The induced EMF E in the loop can be calculated using Faraday's law of electromagnetic induction, which states that the induced EMF is equal to the negative rate of change of magnetic flux through the loop.
Φ=B⋅A
where A is the area of the loop. The area A of the square loop is:
A=d2
E=−dΦdt
The change in flux can be calculated as:
Φright−Φleft=(Bright−Bleft)⋅d2
Substituting the expressions for Bright and Bleft:
Φright−Φleft=(B0(1+x+da)−B0(1+xa))d2
This simplifies to:
Φright−Φleft=B0(da)d2
Now, we can find the induced EMF:
E=−dΦdt=−B0(da)d2dt
Since the loop is moving with velocity v0, we can relate the change in time to the distance traveled:
E=−B0(da)d2⋅1v0
Thus, the induced EMF in the loop is:
E=B0d2v0a
Topper's Solved these Questions
Similar Questions
The magnetic field in a region is given by →B=B0(xa)ˆk. A square loop of side d is placed with its edges along the x and y axes. The loop is moved with a constant velocity →v=v0ˆi The emf induced in the loop is :

View SolutionThe magnetic field existing in a region is given by →B=B0(1+xl)→k. A square loop of edge l and carrying a current I, is placed with its edges parallel to the x-y axes. Find the magnitude of the net magnetic force experienced by the loop.
View Solution
Knowledge Check
The magnetic field in a region is given by →B=B0(1+xa)ˆk. A square loop of edge length 'd' is placed with its edge along X-axis and Y-axis. The loop is moved with a constant velocity →V=V0ˆi. The emf induced in the loop is
Av0B0d2aBv0B0d3aCv0B0d22aD0The magnetic field I nan reigion is given by B=B0XaK. A Squrae edges along the x and y axis. The loop is moved with a constant velocity . The emf induced in the loop is
 AB0v0dBB0v0d22aCB0v0d3a2DB0v0d2a
AB0v0dBB0v0d22aCB0v0d3a2DB0v0d2aA uniform magnetic field existsin region given by →B=3ˆi+4ˆj+5ˆk. A rod of length 5m is placed along y-axis is moved along x- axis with constant speed 1m/sec. Then the magnitude of induced e.m.f in the rod is :
AzeroB25voltC20voltD15volt
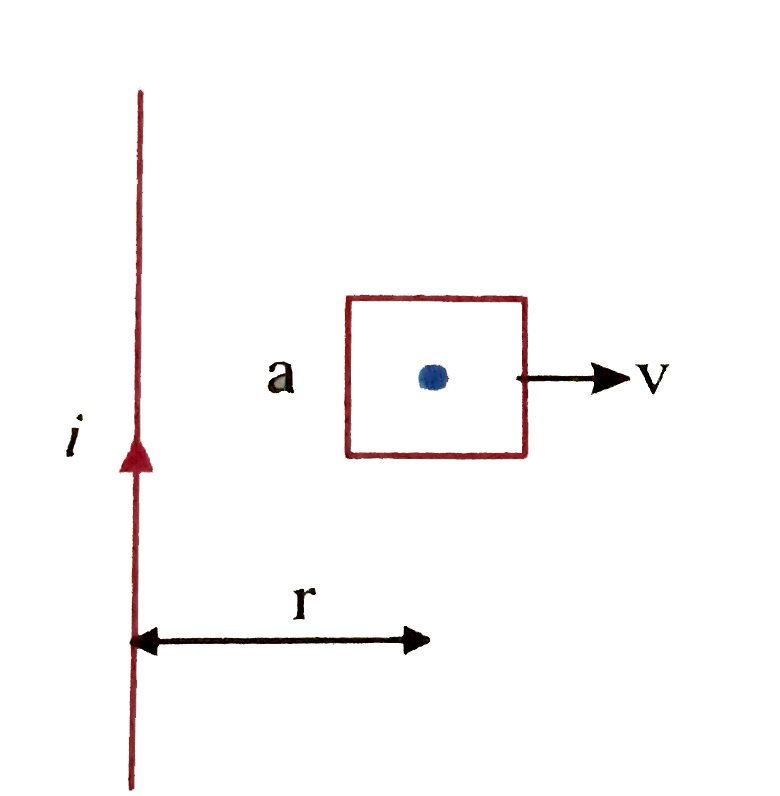
A square loop of side a is placed in the same plane as a long straight wire carrying a current i. The centre of the loop is at a distance r from wire where r>>a. The loop is moved away from the wire with a constant velocity v. The induced e.m.f in the loop is
View SolutionThe magnetic field existing in a region is given by B=B0(1−xy)ˆk, where B0 and l ae constant x is the x coordinate of a point and ˆk is the unit vector along Z axis.A square loop of edge and carrying a current is placed with his edges parallel to the x,y axes.Find the magnitude of the net magnetic force experienced by the loop.
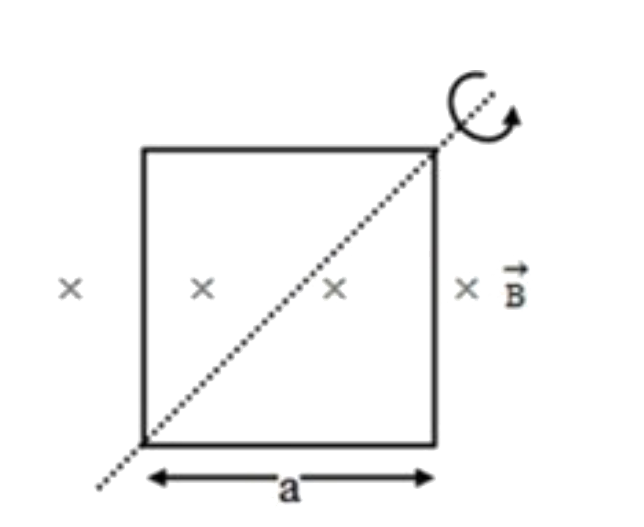
View SolutionA square loop of side a is rotating about its diagonal with angular velocity ω in a perpendicular magnetic field →B It has 10 turns. The emf induced is
View SolutionA conducting circular loop is placed in a magnetic field of strength 0.04 T, such that the plane of the loop is perpendicular to the magnetic field. If the radius of the loop begins to shrink at a constant rate of 0.5mm/s, then calculate the emf induced in the loop when its radius is 1.5 cm.
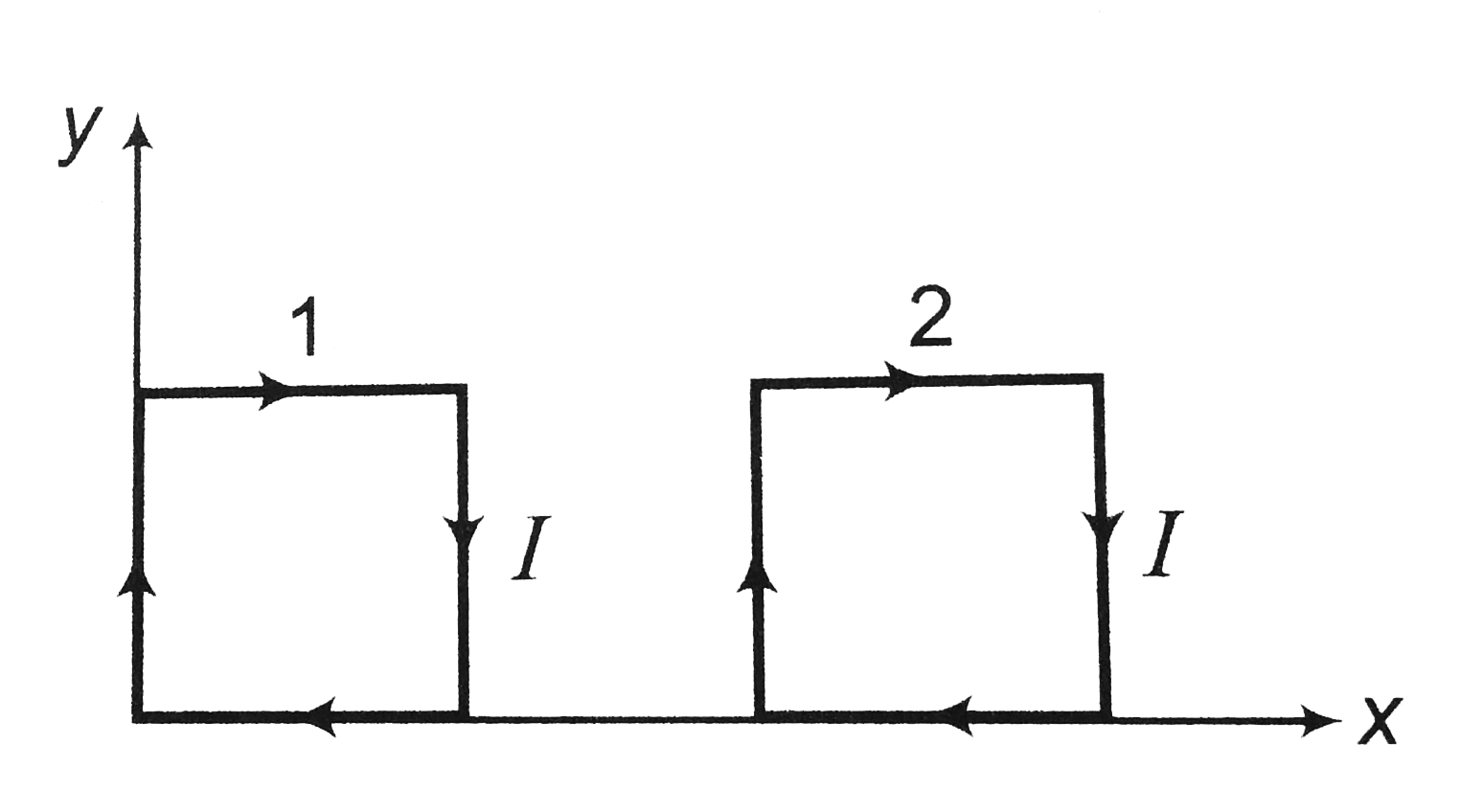
View SolutionMagnetic field in a region is given by B=B0+ˆk. Two loops each of side a is placed in the magnetic region in the xy-plane with one of its sides on x-axis. If F1 is the force on loop 1 and dF2 be the force on loop 2, then
View Solution
