The resistance of a 10 m long potentiometer wire is 10Ω. If the current through it is 0.4 A, what are the balancing lenghts when two cells of emfs 1.3V and 1.1V are connected so as to (i) assist (ii) oppose each other?
To solve the problem, we need to find the balancing lengths when two cells of EMFs 1.3 V and 1.1 V are connected in two different configurations: (i) assisting each other and (ii) opposing each other.
Given Data:
- Length of the potentiometer wire (L) = 10 m
- Resistance of the wire (R) = 10 Ω
- Current through the wire (I) = 0.4 A
- EMF of the first cell (E1) = 1.3 V
- EMF of the second cell (E2) = 1.1 V
Step 1: Calculate the Potential Gradient (k)
The potential gradient (k) is defined as the potential difference per unit length of the wire. It can be calculated using Ohm's law.
1. Calculate the total voltage across the potentiometer wire:
V=I×R=0.4A×10Ω=4V
2. Calculate the potential gradient (k):
k=VL=4V10m=0.4V/m
Step 2: Balancing Length when Cells Assist Each Other
When the cells assist each other, the total EMF (E) is the sum of the individual EMFs:
E=E1+E2=1.3V+1.1V=2.4V
Using the relationship for balancing length:
E=k×l1⟹l1=Ek
Substituting the values:
l1=2.4V0.4V/m=6m
Step 3: Balancing Length when Cells Oppose Each Other
When the cells oppose each other, the total EMF (E) is the difference of the individual EMFs:
E=E1−E2=1.3V−1.1V=0.2V
Using the relationship for balancing length:
E=k×l2⟹l2=Ek
Substituting the values:
l2=0.2V0.4V/m=0.5m
Final Answers:
- Balancing length when cells assist each other (l1) = 6 m
- Balancing length when cells oppose each other (l2) = 0.5 m
- Length of the potentiometer wire (L) = 10 m
- Resistance of the wire (R) = 10 Ω
- Current through the wire (I) = 0.4 A
- EMF of the first cell (E1) = 1.3 V
- EMF of the second cell (E2) = 1.1 V
The potential gradient (k) is defined as the potential difference per unit length of the wire. It can be calculated using Ohm's law.
V=I×R=0.4A×10Ω=4V
k=VL=4V10m=0.4V/m
When the cells assist each other, the total EMF (E) is the sum of the individual EMFs:
E=E1+E2=1.3V+1.1V=2.4V
E=k×l1⟹l1=Ek
Substituting the values:
l1=2.4V0.4V/m=6m
When the cells oppose each other, the total EMF (E) is the difference of the individual EMFs:
E=E1−E2=1.3V−1.1V=0.2V
E=k×l2⟹l2=Ek
Substituting the values:
l2=0.2V0.4V/m=0.5m
- Balancing length when cells assist each other (l1) = 6 m
- Balancing length when cells oppose each other (l2) = 0.5 m
Topper's Solved these Questions
- SOLVED PROBLEMS-II BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SOLVED PROBLEMS-II EXERCISE - Magnetic Effect of Electric Current
13 Videos
- SOLVED PROBLEMS-II BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SOLVED PROBLEMS-II EXERCISE - Magnetism
12 Videos
- SOLVED PROBLEMS-II BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SOLVED PROBLEMS-II EXERCISE - Electrostatics
12 Videos
- SOLVED PROBLEMS - I BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SOLVED PROBLEMS - I EXERCISE - ASSIGNMENTS
24 Videos
- VERY SHORT ANSWER QUESTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - VERY SHORT ANSWER QUESTIONS EXERCISE - COMMUNICATION SYSTEMS
11 Videos
Similar Questions
A potentiometer wire, 4 m long and resistance 10Ω, is connected in series with a resistance of 1988 Ω and a cell of emf 2V and internal resistance 2Ω. What is the potential gradient along the wire?
View Solution(a) Explain the principle of working of a potentiometer.
(b) In a potentiometer, a standard source of emf 5 V and negligible internal resistance maintains a steady current through the potentiometer wire of length wire of length 10 m. Two primary cells of emf E1andE2 are joined together in a series with (i) same polarity and (ii) opposite polarity. The combination is connected to the potentiometer circuit in each case. The balancing length of the wire in the two cases are found to be 700 cm and 100 m , respectively . Find the values of emf of the two cells.
View Solution
Knowledge Check
A potentiometer wire has a length 10m and a resistance 20Ω. Its terminals are connected to a battery of e.m.f. 4V and internal resistance 5Ω. What are the distances at which null points are obtained when two cells of e.m.f.s 1.5V and 1.3 V are connected so as to a ) assist and b) oppose each other ?
A4.75 m, 0.625 mB8.75 m, 6.25 mC8.75 m, 0.625 mD3.75 m, 2.625 mIn given figure, the potentiometer wire AB has a resistance of 5Ω and length 10 m . The balancing length AM for the emf of 0.4 V is
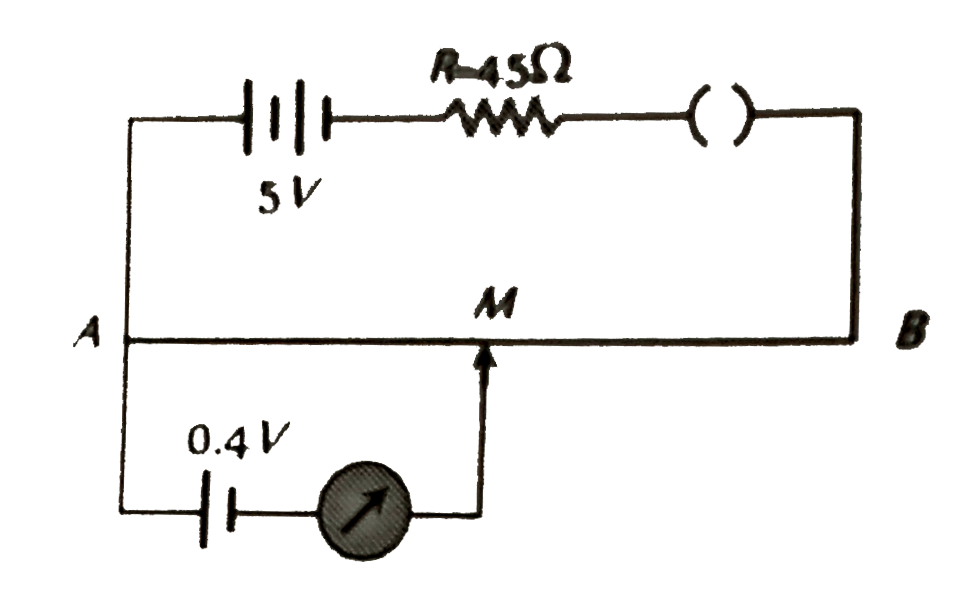 A0.4mB4mC0.8mD8m
A0.4mB4mC0.8mD8mA resistance of potentiometer wire is 1Ω/m. A Daniel cell of e.m.f. 1.08V balances at 216 cm on potentiometer. The current through wire is
A1.5AB0.25AC2.5AD0.5A
Obtain an expression for e.m.f. induced in a coil rotating with uniform angular velocity in a uniform magnetic field. Show graphically the variation of e.m.f. with time (t).
Rewsistance of a potentiometer witre is 0⋅1 Ω/cm. A cell of e.m.f. 1⋅5 V is balanced at 300 cm on this potentiometer wire, Calculate teh current and balancing length for another cell of e.m.f. 1⋅4 V on the same potentiometer wire.
View SolutionThe balancing length for a cell in a potentiometer experiment is 45 cm. In the balanced condition, the current through the potentiometer wire is 2 A. If the total length of the potentiometer wire is 1 m and its total resistance is60Ω , the emf of the cell is (in Volts) _________.
View SolutionA potentiometer wire, 4 m long and resistance 10Ω, is connected in series with a resistance of 1988 Ω and a cell of emf 2V and internal resistance 2Ω. What is the potential gradient along the wire?
View SolutionCell of emf 1 V is connected across a potentiometer, balancing length is 600 cm. What will be the balancing length for 25 V?
View SolutionA cell of e.m.f. of 1.08 V is balanced by a 216 cm length of a potentiometer. What is the length of the wire that would balance a cell of e.m.f. 1.5 V ?
View Solution
