A cell of emf 2V and internal resistance $4 Ω$ is connected across a parallel combination of two resistors of resistance $10 Ω$ and $20 Ω$ . Find the current through each resistor using Kirchhoff's laws.

Video Solution

Text Solution

Verified by Experts

Data: $E = 2 V, r = 4 Ω, R_{1} = 10 Ω, R_{2} = 20 Ω$
Let $I_{1}$ and $I_{2}$ be the current drawn from the cell as shown in the figure.
Then, at node B, by Kirchhoff's current law,
$I - I_{1 - I_{2} = 0}$ or $I = I_{1} + I_{2}$ …………..(i)
Applying Kirchhoff's voltage law to loo ABCEFA, we get,
$- I_{1} R_{1} - I r + E = 0$
$∴ - 10 I_{1} - 4 (I_{1} + I_{2}) + 2 = 0$ ........................ [From Eq.(1)]
$∴ 14 I_{1} + 4 I_{2} = 2$
$∴ 7 I_{1} + 2 I_{2} = I$ ....................(2)

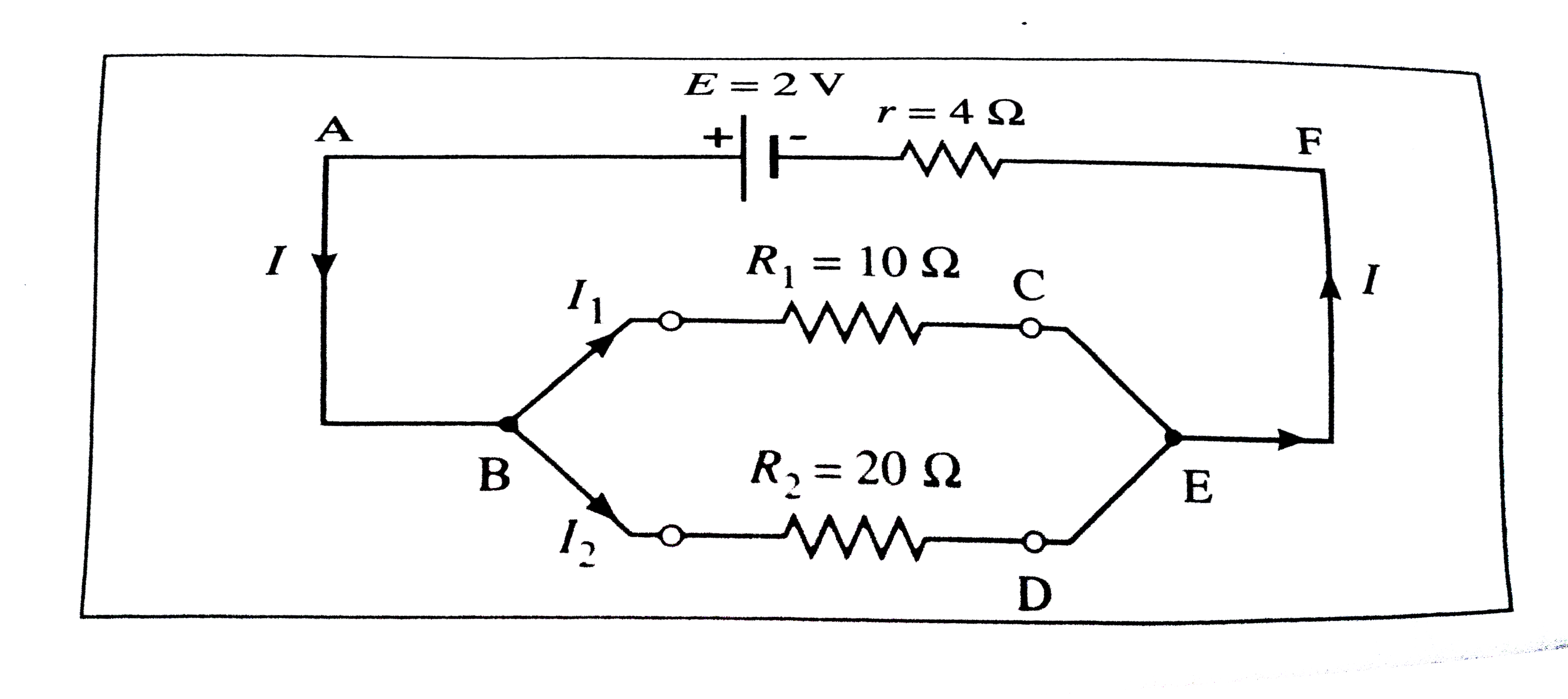
Applying Kirchoff's voltage law to loop BDECB, we get,
$- I_{2} R_{2} + I_{1} R_{1} = 0$
$∴ I_{1} = 2 I_{2}$ ..............(3)
Substitutiing for $I_{1}$ in Eq.(2),
$(7 \times 2) I_{2} + 2 I_{2} = 1$
$∴ 14 I_{2} + 2 I_{2} = 1$
$∴ 16 I_{2} = 1$
$∴ I_{2} = \frac{1}{16} A = 0.0625 A$
Substituting for $I_{2}$ in Eq.(3), we get,
$I_{1} = 2 \times \frac{1}{16} = \frac{1}{8} A = 0.125 A$
$∴ I = I_{1} + I_{2} = 0.125 + 0.0625 = 0.1875$ A

Updated on:21/07/2023

4 cells each of emf 2 V and internal resistance of $1 Ω$ are connected in parallel to a load resistor of $2 Ω$ . Then the current through the load resistor is
A $2 A$
B $1.5 A$
C $1 A$
D $0.888 A$
A voltmeter has a resistance of $50 Ω$ is connected across a cell of e.m.f. 2V and internal resistance $10 Ω$ . The reading of voltmeter is
A1.667V
B16.7V
C167V
D0.167V