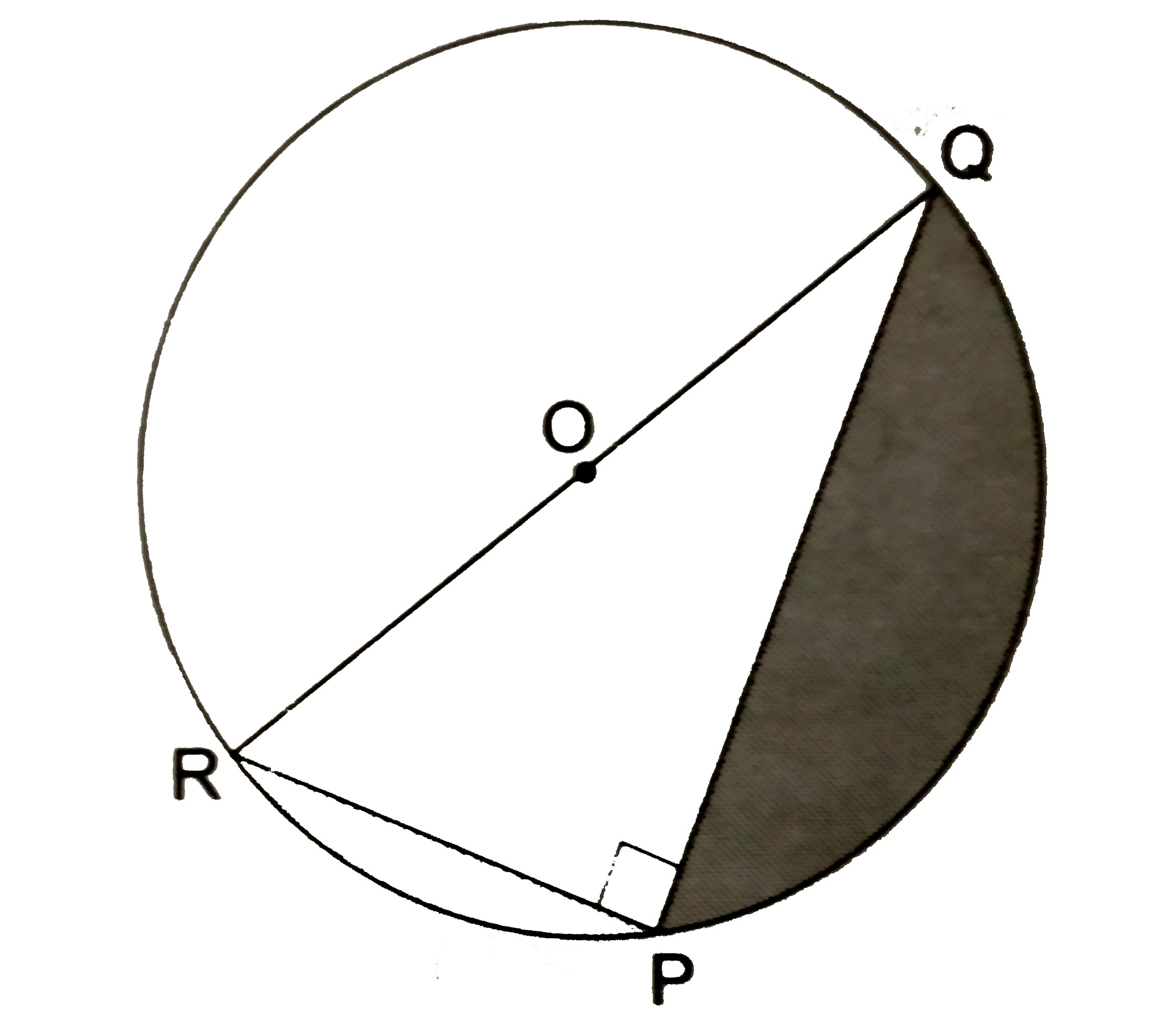
In the figure, O is the centre of the circle.
m(arc PQR)=60∘
OP = 10 cm.
Find the area of the shaded region. (π=3.14,√3=1.73)

The correct Answer is:9.08cm2
The radius of the circle ( r) = OP = 10 cm
m(arc PQR)=θ=60∘
The shaded region is segment PQR.
A(segment PQR) =r2[πθ360−sinθ2]
=102[3.14×60360−sin602]
=100[3.146−√32×2]...[∵sin60=√32]
100×[3.146−1.734]...(∵√3=1.73)
=100[3.14×2−1.73×312]
=100[6.28−5.1912]
=100×1.0912=10912
=9.083≈9.08cm2
Topper's Solved these Questions
- MENSURATIONBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:MENSURATIONExercise:8.5
Explore 4 Videos
- MENSURATIONBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:MENSURATIONExercise:Assignment 8.1
Explore 9 Videos
- MENSURATIONBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:MENSURATIONExercise:8.3
Explore 11 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:4 Marks Questions
Explore 18 Videos
- MODEL QUESTION PAPERBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:MODEL QUESTION PAPERExercise:SOLVE THE FOLLOWING SUBQUESTIONS: (ANY ONE)
Explore 2 Videos
Similar Questions
find the area of the shaded region [Use π=3.14] .
View SolutionFind the area of the shaded region. (π=227), √3=1.73)
View SolutionIn the adjoining figure, O is the centre of the circle.
m(arc PQR) =60∘ OP=10 cm
Find the area of the shaded region.

Given θ=60∘,r=10cm
π=3.14,√3=1.73
To find: A(shaded region)
View SolutionIn figure, find the area of the shaded region [Useπ=3.14]
View SolutionIn figure , AB is a diameter of the circle, AC = 6cm and BC = 8cm . Find the area of the shaded region . (use π=3.14)

View SolutionIn the given figure PQ=24cm,PR=78cm and O is the centre of the circle. Find the area of the shaded region. [Take π=3.14]
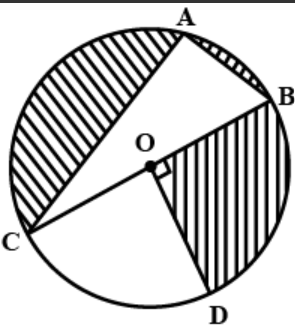
View SolutionIn Figure , O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD=90°. Find the area of the shaded region.[Useπ=3⋅14]
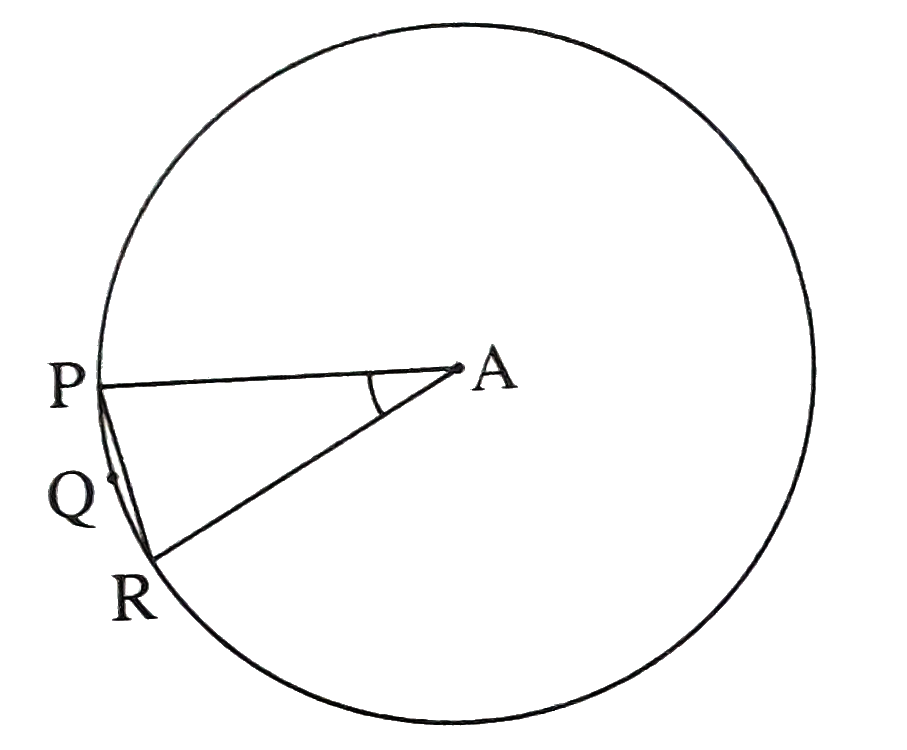
View SolutionIn the figure, if A is the centre of the circle. ∠PAR=30∘, AP=7.5,
find the area of the segment PQR. (π=3.14)
View SolutionIn the given figure O is the centre of the circle with AC=24cm,AB=7cm and ∠BOD=90∘. Find the area of shaded region.
[Use π=3.14]

View SolutionIn the given figure, PQ = 24 cm PR = 7 cm and O is the centre of the circle. Find the area of the shaded region. (Use π=3.14)

View Solution

