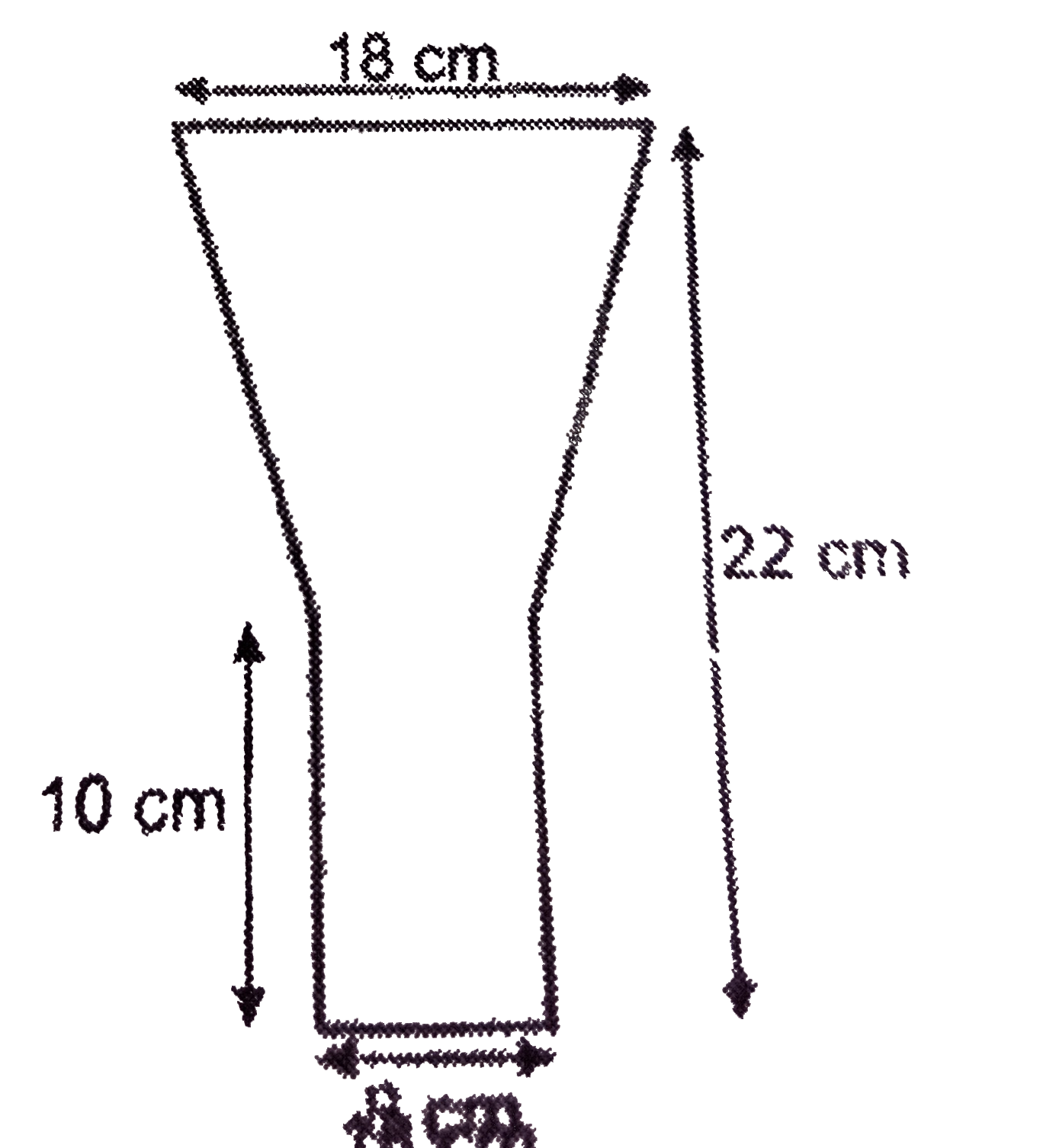
An oil funnel of tin sheet consists of a cylindrical portion 10 cm long attached to a frustum of cone. The diameters of the top and bottom of the frustum are 18 cm and 8 cm respecti8vely. If the slant height of the frustum of the cone is 13 cm, find the area of the tin required to make the funnel from the given information in the figure
$(π = 3.14)$

Video Solution

Text Solution

Verified by Experts

Here, radius (r ) of the cylinder = 4 cm height (h) of the cylinder = 10 cm
slant height (l) of the frustum 13 cm
$R_{1} and R_{2}$ of the frstum are 9 cm and 4 cm respectively
Tin required to make the funnel = Curved surface area of the cylindrical portion + Curved surface area of the frustum portion
(The curved surface area) of cuylindrical portion
$= 2 π r h ... (Formula)$
$= 2 π \times 4 \times 10 c m^{2} ... (substituting the given values) ... (1)$
(the curved surface area) of the frustum portion
$= π (R_{1} + R_{2}) l ... (Formula)$
$= π (9 + 4) \times 13 ... (Substituting the given values)$
$= π \times 13 \times 13 c m^{2} ... (2)$
$∴$ tin required $= 2 π \times 4 \times 10 + π \times 13 \times 13 ... [From (1) and (2)]$
$= 80 π + 169 π$
$= π (80 + 169)$
$= 3.14 \times 249 = 781.86 c m^{2}$
The tin required to make the funnel is $781.86 c m^{2}$

Updated on:21/07/2023

The radii of the ends of a frustum of a cone 40 cm high are 38 cm and 8 cm. The slant height of the frustum of cone is
A50 cm
B $10 \sqrt{7} c m$
C $60.96 c m$
D $4 \sqrt{2}$
If the slant height of the frustum of a cone is 10 cm and its perpendicular height is 8 cm then what is the difference of radii of the circular bases?
A8 cm
B2 cm
C10 cm
D6 cm
A bucket is in the form of a frustum of a cone and holds 28.490 litres of water. The radii of the top and bottom are 14 cm and 21 cm respectively. Find the height of the bucket.
A29.2 cm
B10 cm
C20.9 cm
D25 cm