In the figure, is a rectangle. , XL = 10. 5 cm. Diamter of the smaller semicircle is half the diameter of larger semicircle. Find the area of non-shaded region.

Let, diameter of smaller semicircle = 2r
Diameter of larger semicircle = 4r
Now LM = 21 cm
Radius of a smaller semicircle = r = 3.5 cm
and radius of larger semicircle (R) =
Now area of smaller semicircle
Area of larger semicircle
Now area of rectangle
Area of non-shaded region = Area of rectangle - (Area of smaller semicircle + Area of larger semicircle)
= 2220.50 - (19.25 + 77)
=124.25 cm^2124.25 cm^2
Topper's Solved these Questions
- MENSURATIONBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:MENSURATIONExercise:8.5
Explore 4 Videos
- MENSURATIONBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:MENSURATIONExercise:Assignment 8.1
Explore 9 Videos
- MENSURATIONBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:MENSURATIONExercise:8.3
Explore 11 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:LINEAR EQUATIONS IN TWO VARIABLESExercise:4 Marks Questions
Explore 18 Videos
- MODEL QUESTION PAPERBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:MODEL QUESTION PAPERExercise:SOLVE THE FOLLOWING SUBQUESTIONS: (ANY ONE)
Explore 2 Videos
Similar Questions
Knowledge Check
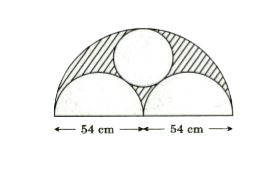
In the given figure there are 3 semicircles , the radii of each smaller circle is equal. If the radius of the larger circle be 22 cm , then the area of the shaded region is :
 A363π4B363π3C236.5πD363π
A363π4B363π3C236.5πD363π
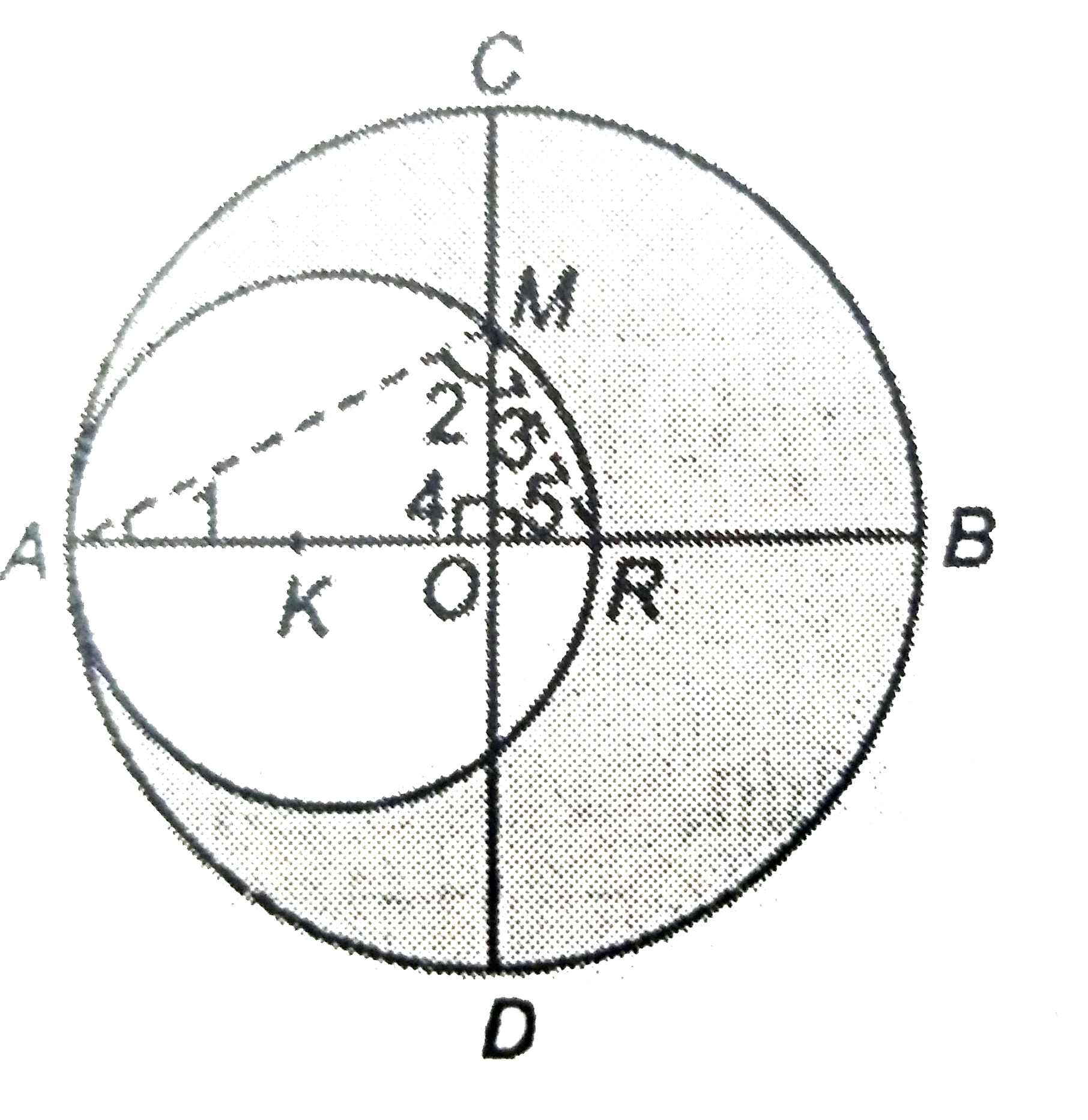
In the adjoining figure, CM = 5 cm, RB = 9 cm, CD⊥AB, O is the centre of larger circle and K is the centre of smaller circle. Find the area of shaded region
View SolutionIn given figure a semicircle of radius 7cm is inscribed in a rectangle. Find the area of the shaded region.
View SolutionABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
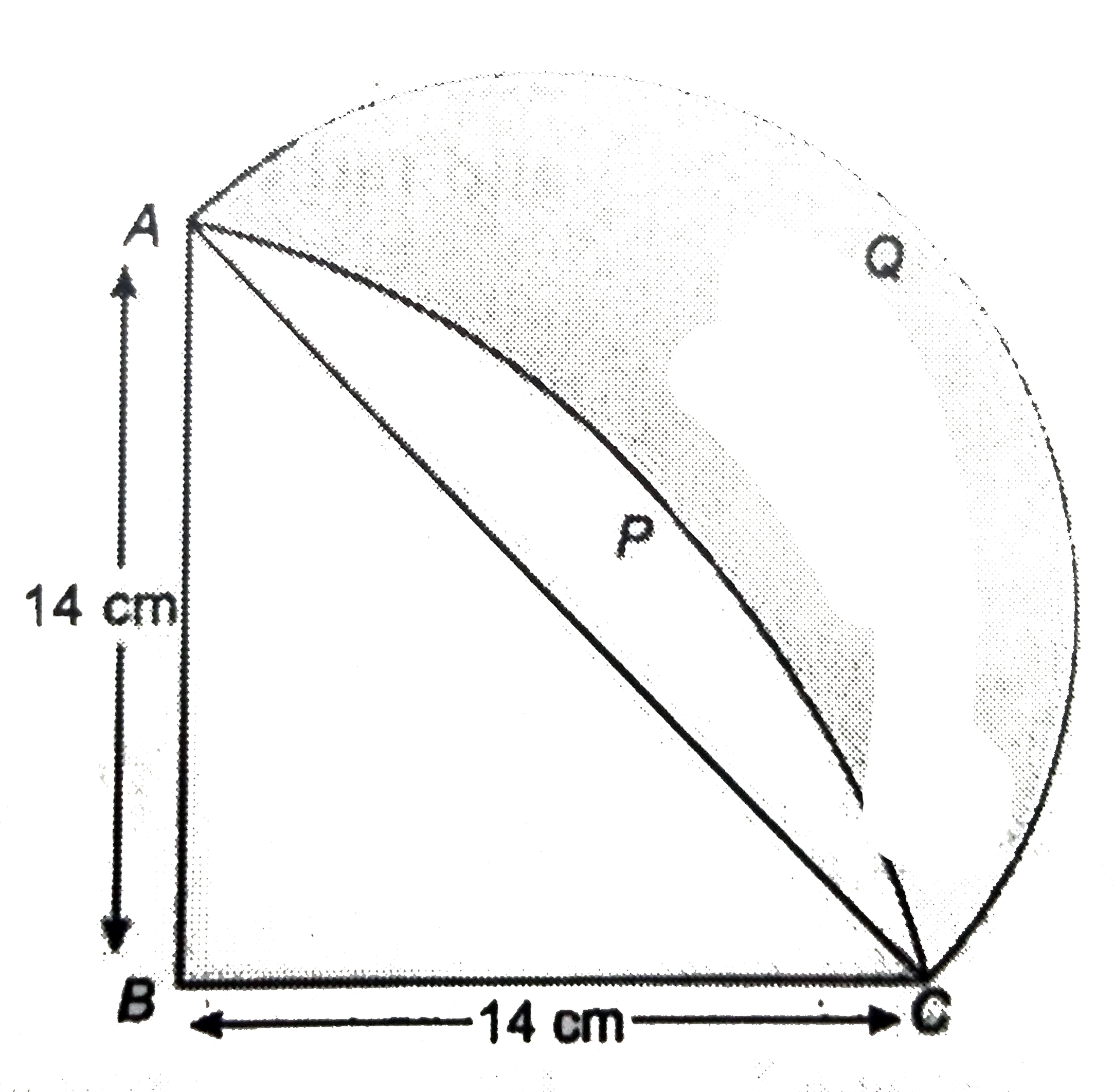
View SolutionABCD is a square of 10 cm and semicircles are drawn with each side of the square as diameter. Find the area of the shaded region. (π=3.14)
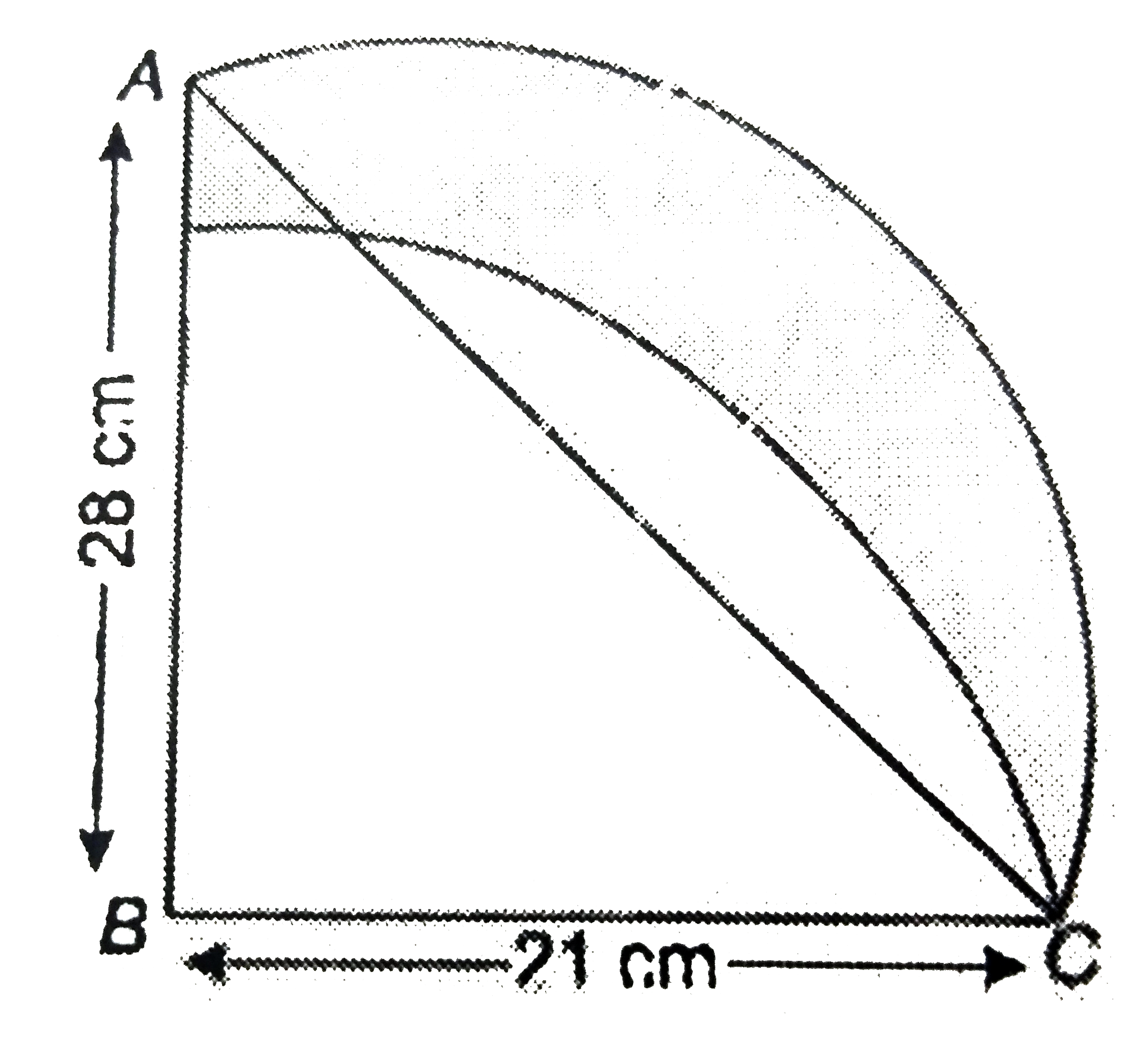
View SolutionIn the figure, in ΔABC,∠B=90∘,AB=28cmandBC=21cm. With AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region correct to two decimal places.
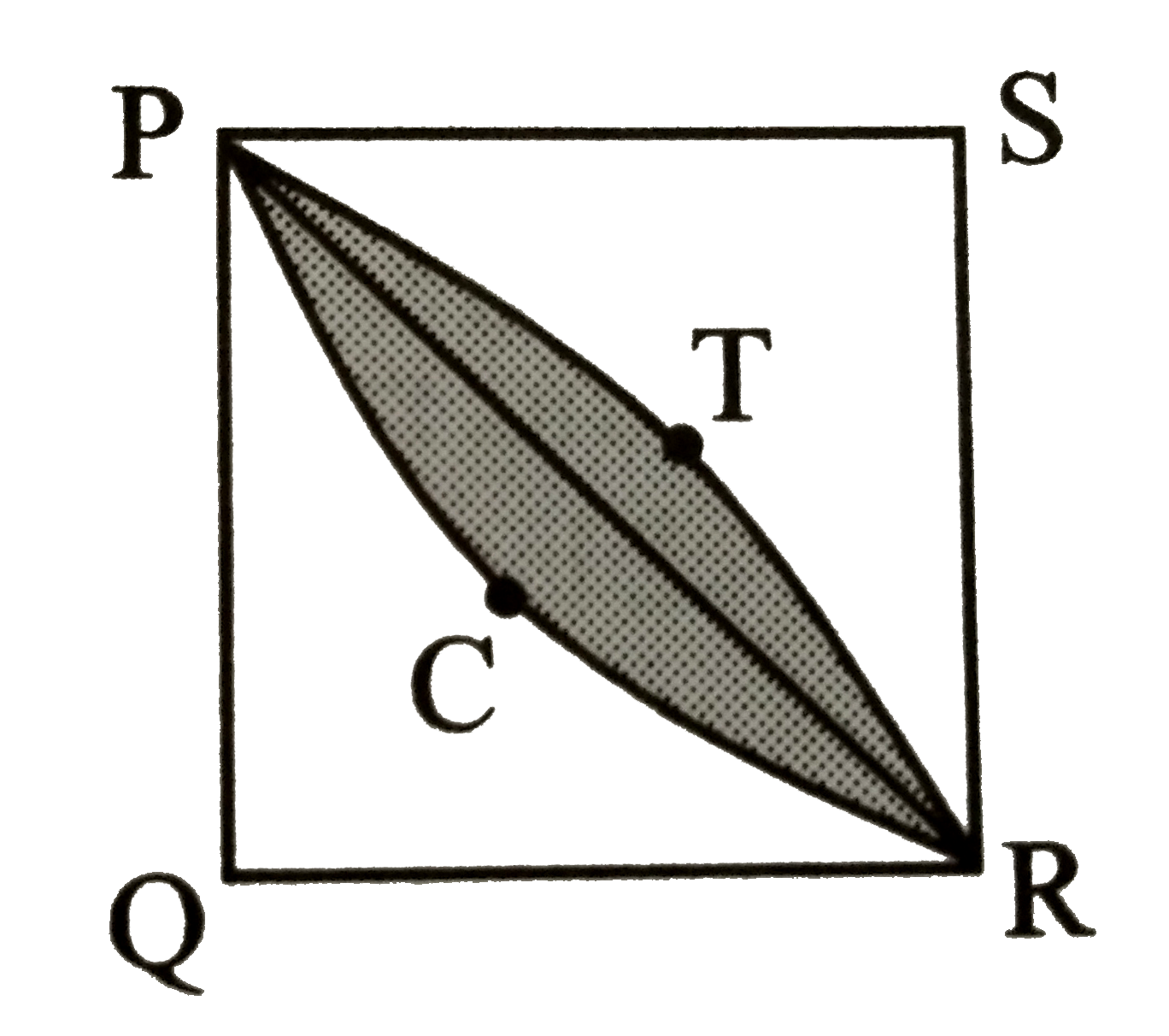
View SolutionIn the given figure, if □PQRS is a square of side 10 cm, then find the area of the shaded region.
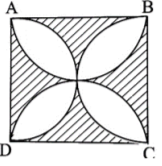
View SolutionIn the figure, ABCD is a square of side 14 cm. Semi-circles are drawn with each side of square as diameter. Find the area of the shaded region.
View Solution