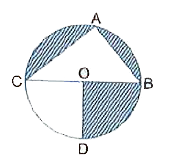
In figure , AB is a diameter of the circle, AC = 6cm and BC = 8cm . Find the area of the shaded region . (use π=3.14)

Given, AC = 6cm and BC = 8cm
we know that, triangle in a semi-circle with hypotenuse as diameter is right angled triangle.
∴∠C=90∘
In right angled ΔACB, use pythagoras theorem,
∴AB2=AC2+CB2
⇒AB2=62+82=36+64
⇒AB2=100
⇒ AB = 10cm [since, side cannot be negative]
∴ Area of ΔABC=12×BC×AC=12×8×6=24cm2
Here , diameter of circle, AB = 10cm
∴ Radius of circle, r = 102=5cm
Area of circle = πr2=3.14×(5)2
= 3.14×25=78.5cm2
∴ Area of the shaded region = Area of circle - Area of ΔBC
= 78.5−24=54.5cm2
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the given figure, AC is a diameter of a circle with radius 5 cm. if AB=BC and CD=8 cm, the area of the shaded region to the nearest whole number is
 A28 cm2B29 cm2C30 cm2D45 cm2
A28 cm2B29 cm2C30 cm2D45 cm2
In Figure , O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD=90°. Find the area of the shaded region.[Useπ=3⋅14]
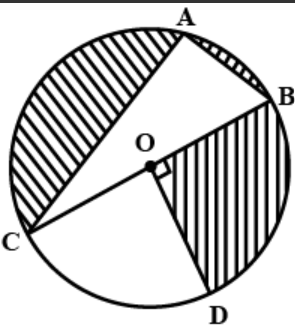
View SolutionIn the given figure O is the centre of the circle with AC=24cm,AB=7cm and ∠BOD=90∘. Find the area of shaded region.
[Use π=3.14]

View SolutionIn the adjoining figure, find the area of the shaded region (Use π=3.14)
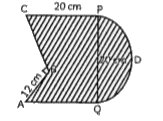
View SolutionIn the figure, PDQ is a semicircle of diameter 20 cm, CP = AQ = 20 cm and AB = 12 cm. If AB ⊥ BC, find the area of the shaded region. (Use π = 3.14)
View SolutionIn the given figure, O is the centre of the bigger circle and AC is its diameter. Another circle with AB as diameter is drawn. If AC = 54 cm and BC = 10 cm. Find the area of the shaded region

View SolutionIn the given figure, PQ = 24 cm PR = 7 cm and O is the centre of the circle. Find the area of the shaded region. (Use π=3.14)

View SolutionIn the given Fig, O is the centre of the circle with AC=24cm,AB=7cmand∠BOD=90∘. Find the area of the shaded region [Take π=3.14 ]
View Solution

