D, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC and O is any point in the plane of △ABC. Show that (1)¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF=¯0
Step by step video & image solution for D, E, F are the midpoints of the sides BC, CA and AB respectively of triangleABC and O is any point in the plane of triangleABC. Show that (1) bar(AD)+bar(BE)+bar(CF)=bar(0) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTORSBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:VECTORSExercise:Multiple choice question
Explore 10 Videos
- VECTORSBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:VECTORSExercise:Theory Questions
Explore 4 Videos
- TRIGONOMETRIC FUNCTIONS Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:TRIGONOMETRIC FUNCTIONS Exercise:Multiple Choice Questions
Explore 12 Videos
Similar Questions
D,E,F are the midpoints of the sides ¯¯¯¯¯¯BC,¯¯¯¯¯¯CAand¯¯¯¯¯¯AB respectively of the triangle ABC. If P is any point in the planeof the triangle, show that −−→PA+−−→PB+−−→PC=−−→PD+−−→PE+−−→PF.
View SolutionIf G is the centroid of △ABC and O is any point in the plane of △ABC, show that
(1) ¯¯¯¯¯¯GA+¯¯¯¯¯¯GB+¯¯¯¯¯¯GC=¯0
(2) ¯¯¯¯¯¯OA+¯¯¯¯¯¯OB+¯¯¯¯¯¯OC=3¯¯¯¯¯¯OG.
View Solution
Knowledge Check
Let D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
A0B0C2DNone of theseIf D,E and F are the mid-points of the sides BC,CA and AB, respectively of a ΔABC and O is any point, show that
(i) AD+BE+CF=0
(ii) OE+OF+DO=OAAA. a zero vectorBB. a unit vectorCC. 0DD. none of theseIn a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A−−→BE+−−→CFB−−→BE−−−→CFC−−→CF−−−→BED−−−→BE−−−→CF
If D, E, F are the mid points of the side BC, CA and AB respectively of a triangle ABC, write the value of →AD+→BE+→CF.
View Solutionif D,E and F are the mid-points of the sides BC,CA and AB respectively of the ΔABCandO be any points, then prove that OA+OB+OC=OD+OE+OF
View SolutionIf D, E and F be the middle points of the sides BC,CA and AB of the ΔABC, then AD+BE+CF is
View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC. Prove that
(i) BDEF is a ||gm,
(ii) ar(△DEF)=14ar(△ABC)and
(iii) ar(||gm BDEF)=12ar(△ABC)
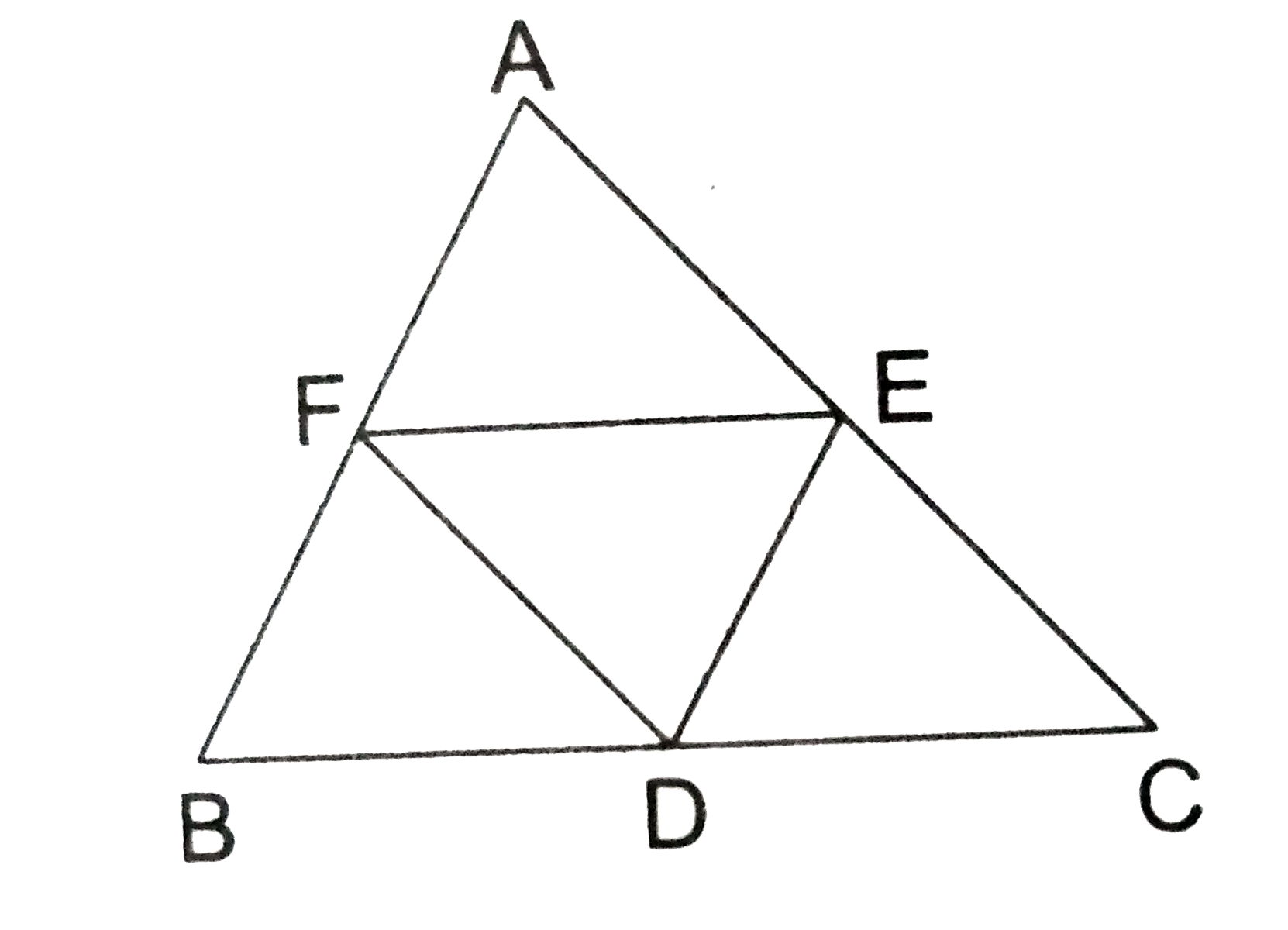
View SolutionIf D, E, F are the mid-points of the sides BC, CA and AB respectively of △ABC, then ¯¯¯¯¯¯AD+23¯¯¯¯¯¯BE+13¯¯¯¯¯¯CF=
View Solution

