D, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC. Prove that
(i) BDEF is a ||gm,
(ii) ar(△DEF)=14ar(△ABC)and
(iii) ar(||gm BDEF)=12ar(△ABC)
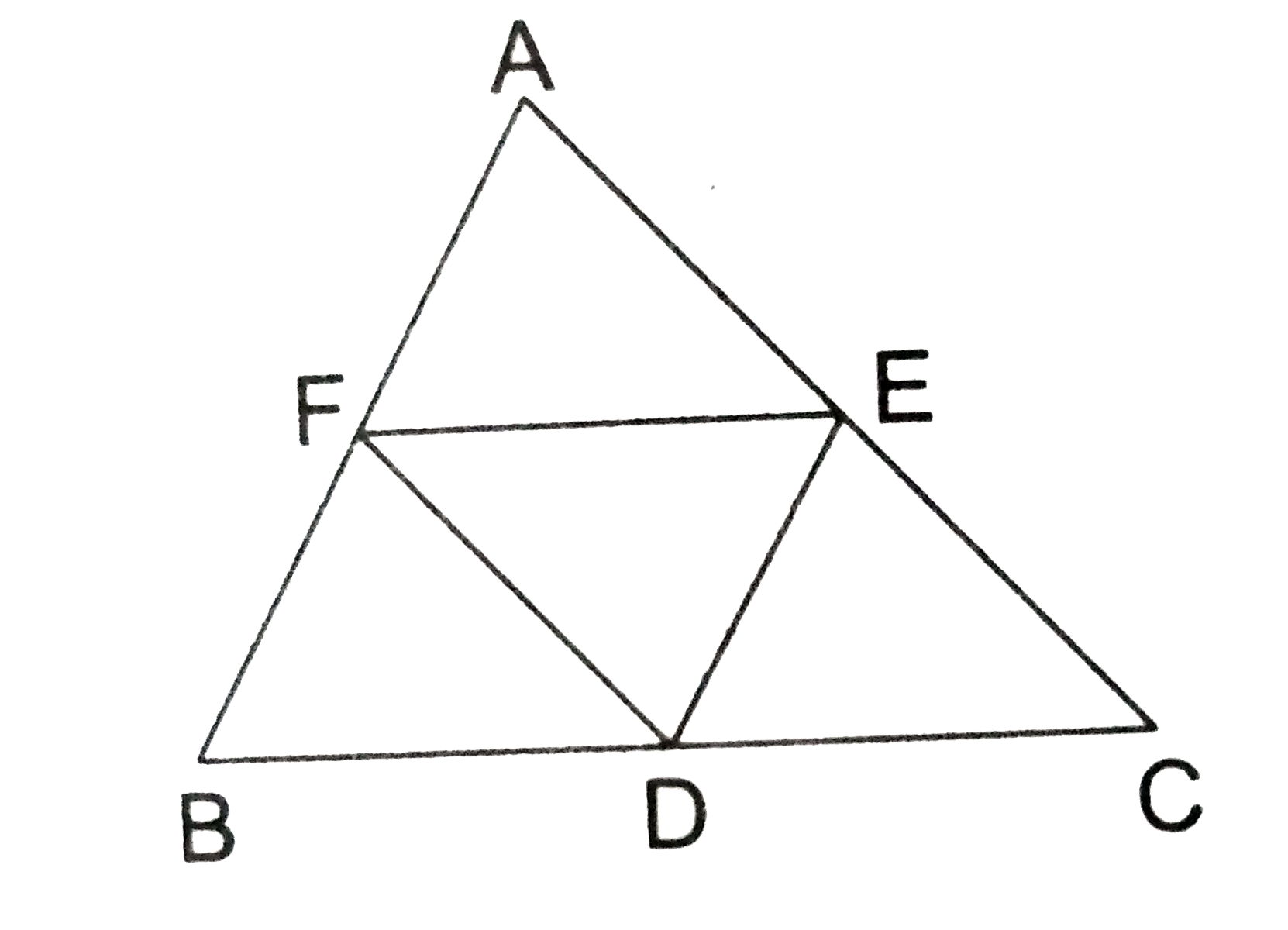
By midpoint theorem, DE||BA and EF||BC.
∴DE||BF and FE||BD.
∴BDEFisa∣∣gm.
Similarly, AFDE is a ||gm.
And, DCEF is ||gm.
Diagonal DF of ||gm BDEF divides it into two △ of equal area.
∴ar(△DEF)=ar(△BDF).
Similarly, ar(△DEF)=ar(△DCE).
And, ar(△DEF)=ar(△AFE).
∴ar(△DEF)=ar(BDF)=ar(△DCE)=ar(△AFE)
∴ar(△DEF)=14ar(△ABC).
=2×14×ar(△ABC)=12×ar(△ABC).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES Book:RS AGGARWALChapter:AREAS OF PARALLELOGRAMS AND TRIANGLES Exercise:Exercise 11
Explore 38 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES Book:RS AGGARWALChapter:AREAS OF PARALLELOGRAMS AND TRIANGLES Exercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBook:RS AGGARWALChapter:AREAS OF TRIANGLES AND QUADRILATERALSExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
Similar Questions
D, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogram
View SolutionD, E and F are respectively the mid -points of the sides BC, CA and AB of a △ABC .Show that (i) BDEF is a parallelogram
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC. Prove that:
(i) □BDEF is a parallelogram
(ii) area of ΔDEF=14× area of ΔABC
(iii) area of □BDEF=12× area of ΔABC

View SolutionD, E, F are the midpoints of the sides BC, CA and AB respectively of △ABC and O is any point in the plane of △ABC. Show that (1)¯¯¯¯¯¯AD+¯¯¯¯¯¯BE+¯¯¯¯¯¯CF=¯0
View Solutionlf D, E and F are respectively the midpoints of the sides BC, CA and AB of an equilateral triangle ABC, prove that △DEF is also an equilateral triangle.
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(BDEF) =12ar(△ABC)
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of aΔABC.Show that (i) BDEF is a parallelogram. (ii) ar (DEF)=14ar (ABC)(iii) ar (BDEF)=12ar (ABC)
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(△DEF)=14ar(△ABC)
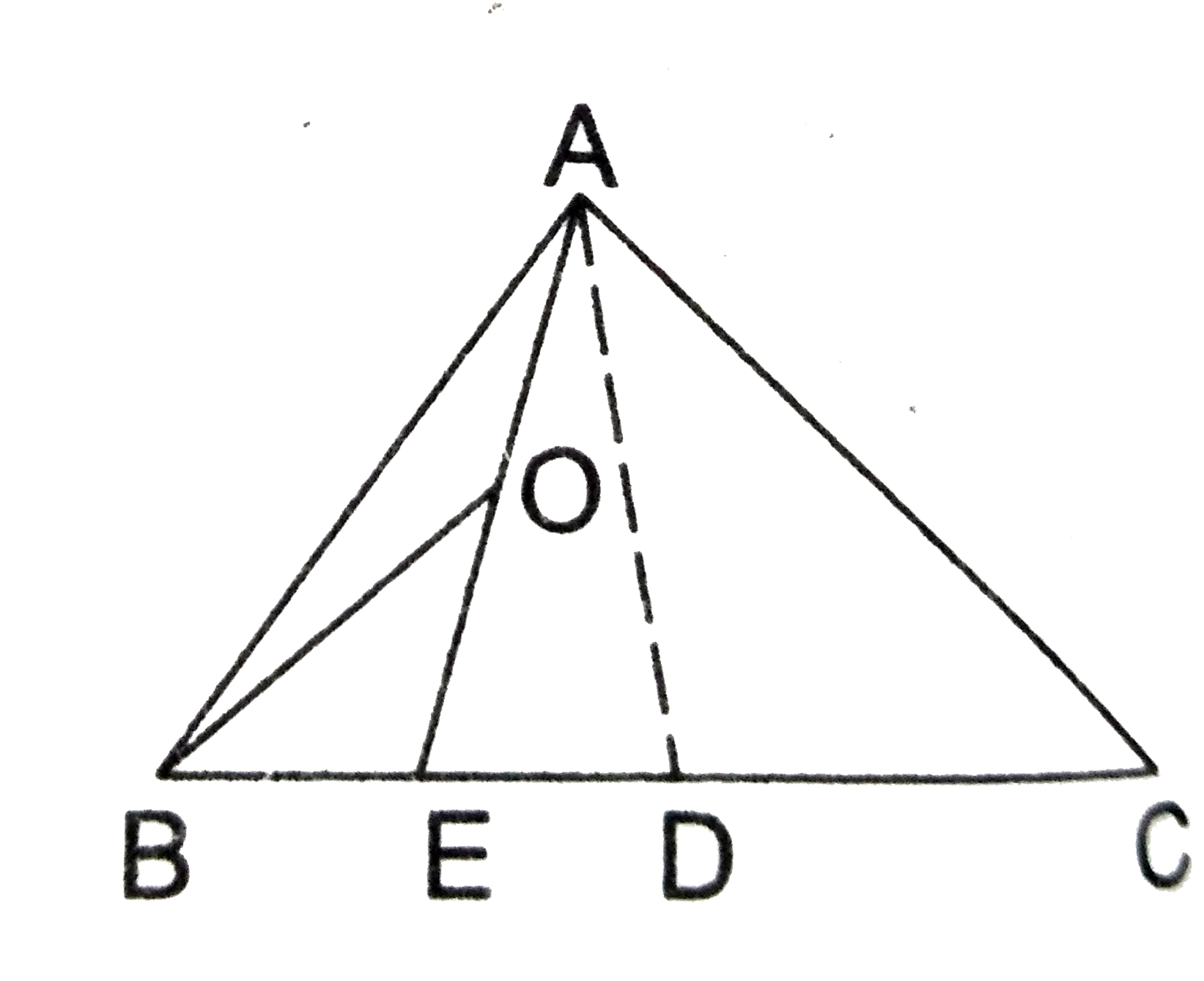
View SolutionD is the midpoint of side BC of △ABC and E is the midpoint of BD. If O is the midpoint of AE,
prove that ar(△BOE)=18ar(△ABC).
View SolutionIf D,E and F are the midpoints of sides BC, CA, and Ab respectively of △ABC then using coordinate geometry prove that Area of △DEF= 14 (Area of △ABC)
View Solution