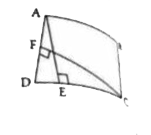
Assertion (A) : In the given figlure, ABCD is a ||gm in which DE⊥ADandBF⊥AD. If AB = 16 cm, DE = 8 cm and BF = 10 cm then what is the length of AD?.
Both Assertion (A) and Reason (R ) are true and Reason (R ) is a correct explansion of Assertion (A).
Both Assertion (A) and Reason (R ) are true but Reason (R ) is not a correct explansion of Assertion (A).
Assertion (A) is true and Reason (R ) is false.
Assertion (A) is false and Reason (R ) is true.
The correct Answer is:D
Reason (R ) is clearly true.
Area of ||gm =Ab×DE=AD×BF.
Let AD = x cm. Then,
16×8=×x×10⇒x=16×810=12.8cm.
But, AD is 12 cm.
∴ Assertion (A) is false.
Thus, Assertion (A) is false and Reason (R ) is true.
So, the correct answer is (d).
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES Book:RS AGGARWALChapter:AREAS OF PARALLELOGRAMS AND TRIANGLES Exercise:MULTIPLE-CHOICE QUESTIONS (MCQ)
Explore 32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBook:RS AGGARWALChapter:AREAS OF TRIANGLES AND QUADRILATERALSExercise:Multiple Choice Questions (Mcq)
Explore 16 Videos
Similar Questions
Knowledge Check
In figure, ABCD is a parallelogram, AE⊥DC and CF⊥AD. If AD = 12 cm, AE = 8 cm and CF= 10 cm find CD.
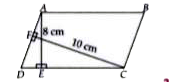 A17 cmB12 cmC10 cmD15 cm
A17 cmB12 cmC10 cmD15 cmIn the given figure, ABCD is a ||gm in which DL⊥AB. IF AB = 10 cm and DL = 4 cm then the ar(||gm ABCD) = ?
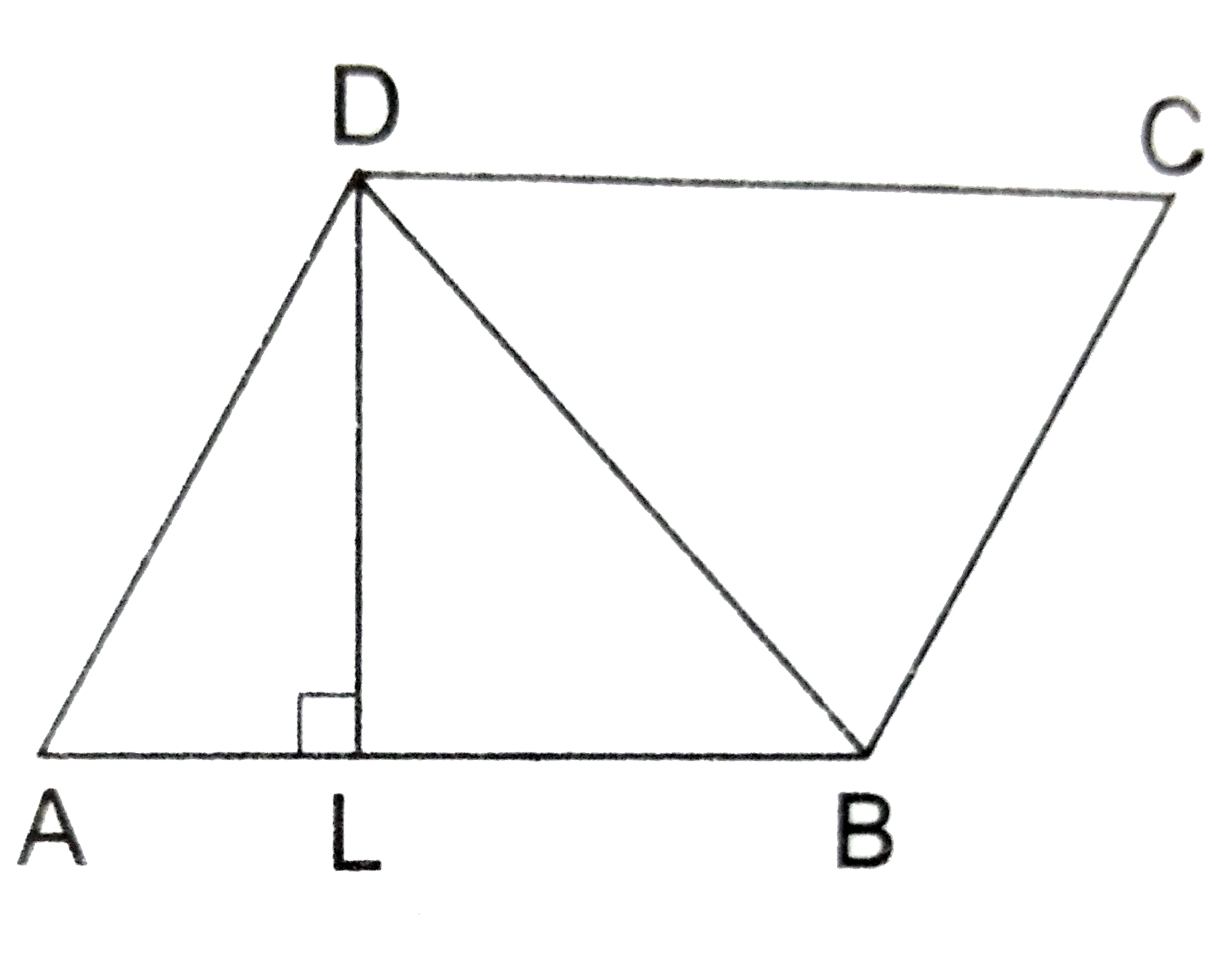 A40cm2B80cm2C20cm2D196cm2
A40cm2B80cm2C20cm2D196cm2In the given figure, ABCD is a trapezium such that AL⊥DCandBM⊥DC. If AB=7cm,BC=AD=5cm and AL=BM=4cm then ar(trap.ABCD)=?
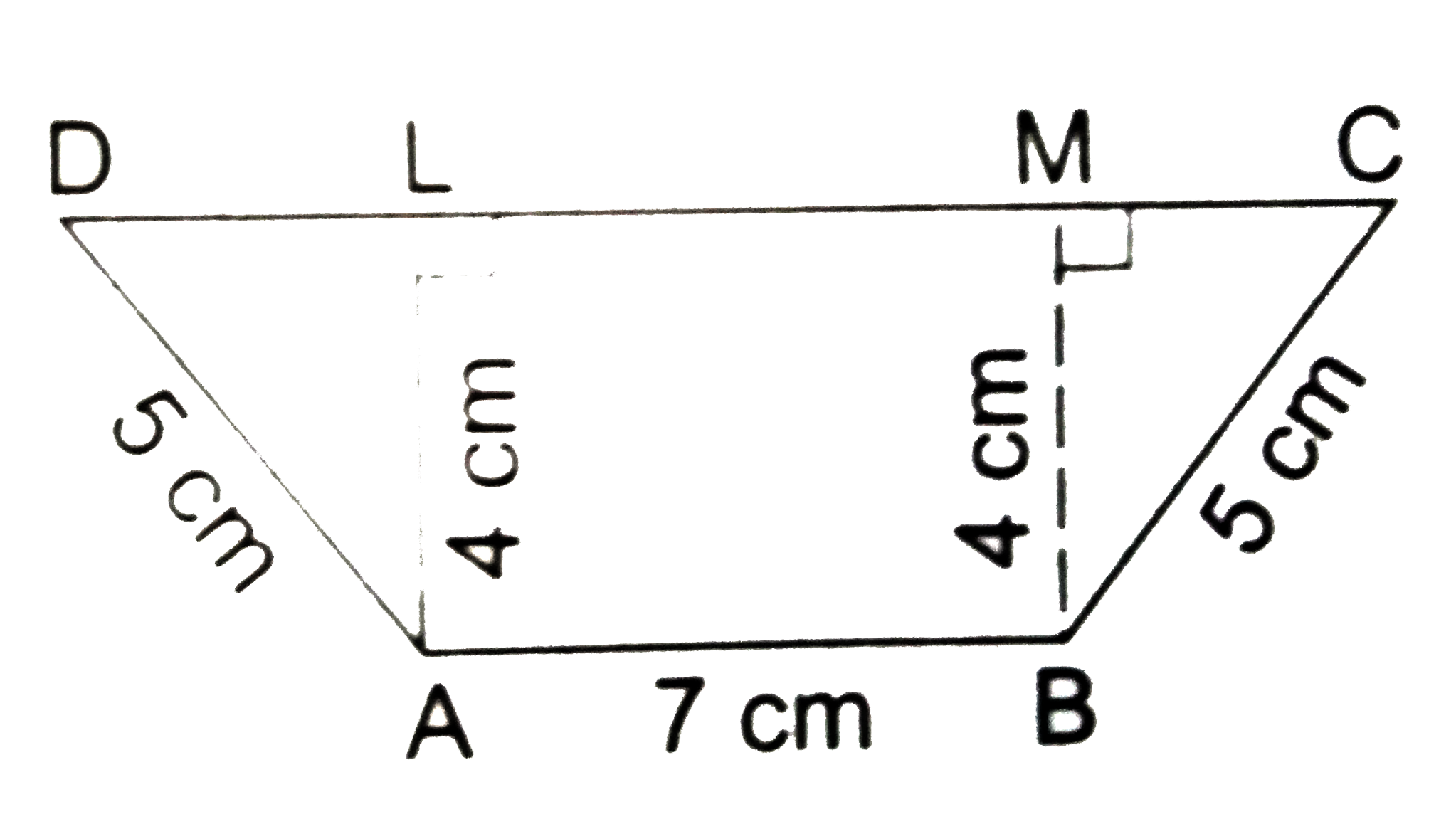 A24cm2B40cm2C55cm2D27.5cm2
A24cm2B40cm2C55cm2D27.5cm2
In the given figure, ABCD is a || gm in which DL⊥AB. If AB = 10 cm and DL = 4 cm, then the area of || gm ABCD = ?

View SolutionIn the given figure, ABCD is a parallelogram, AE⊥DC and CF⊥AD. If AB=16cm, AE=8cm and CF=10cm, find AD.
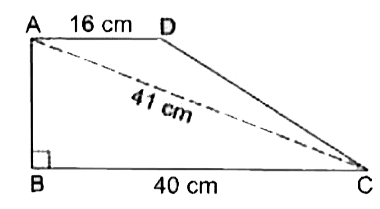
View SolutionIn the given figure, ABCD is a trapezium in which AD∣∣BC,∠ABC=90∘,AD=16cm,AC=41cm and BC = 40 cm. Find the area of the trapezium.
View SolutionIn △ABC, AB = 6 cm, AC = 8 cm, and BC = 9 cm. The length of median AD is:
View SolutionIn △ABC,AB=6cm,AC=8cm,andBC=9cm. The length of median AD is :
View Solution