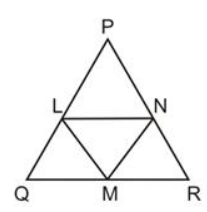
Let □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
Let ¯p,¯q,¯r,¯s,¯¯¯m and ¯n be the position vectors of the points P,Q,R, S,M and N respectively. M and N are the midpoints of PQ and RS respectively.

∴¯¯¯m=¯p+¯q2and¯n=¯r+¯s2
∴¯¯¯¯¯PS+¯¯¯¯¯¯QR=(¯s−¯p)+(¯r−¯q)
=¯s−¯p+¯r−¯q
=2(¯r+¯s2)−2(¯p+¯q2)
=2¯n−2¯¯¯m
=2(¯n−¯¯¯m) ∴¯¯¯¯¯PS=¯¯¯¯¯¯QR=2MN.
Topper's Solved these Questions
- VECTORSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - VECTORSEXERCISE - Theory Questions
4 Videos
- VECTORSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - VECTORSEXERCISE - Examples for Practics
28 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Multiple Choice Questions
12 Videos
Similar Questions
Knowledge Check
OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3OPQR is a square with M and N as the middle points of the sides PQ and QR, respectively. The ratio of the areas of the square and the triangle OMN is
A4:1B2:1C8:3D4:3PQRS is a rectangle, A, B, C and D are the mid points of sides PQ, QR, RS and PS respectively. If area of ΔPQR is 48 cm2, then what is the area (in cm2) of ΔBCD?
A24B6C16D12
□PQRS is a reactangle. If A, B and C are the mid-points of PQ, PS and QR respectively, then prove that
AB+AC=12(PR+SQ).
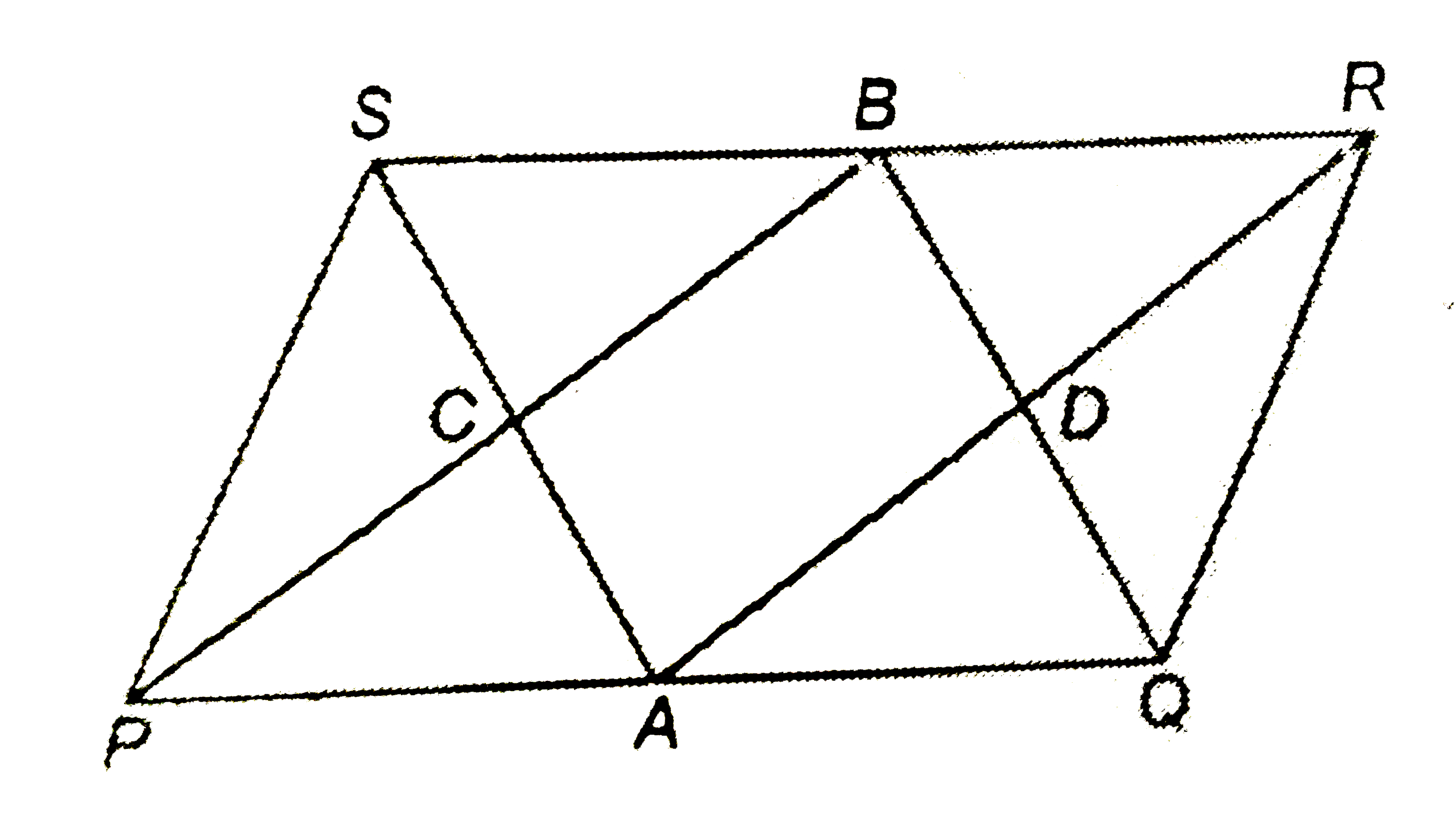
View SolutionIn the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
View SolutionΔPQR is right angled at Q. If x & y are the mid-points of sides PQ & QR respectively. Then which one is not true of the following:
View SolutionPQRis a triangle such that PQ=PR.RSand QT are the medians to the sides PQandPR respectively. If the medians RS and GT intersect at right angle, then what is the value of (PQQR)2 ?
View SolutionPQRSis a rectangle. Points A, B, C and D are the mid points of sides PQ,QR,RSandPSrespectively. If area of ΔPQR is 48cm2, then what is the area (in cm) of ΔBCD?
View Solution