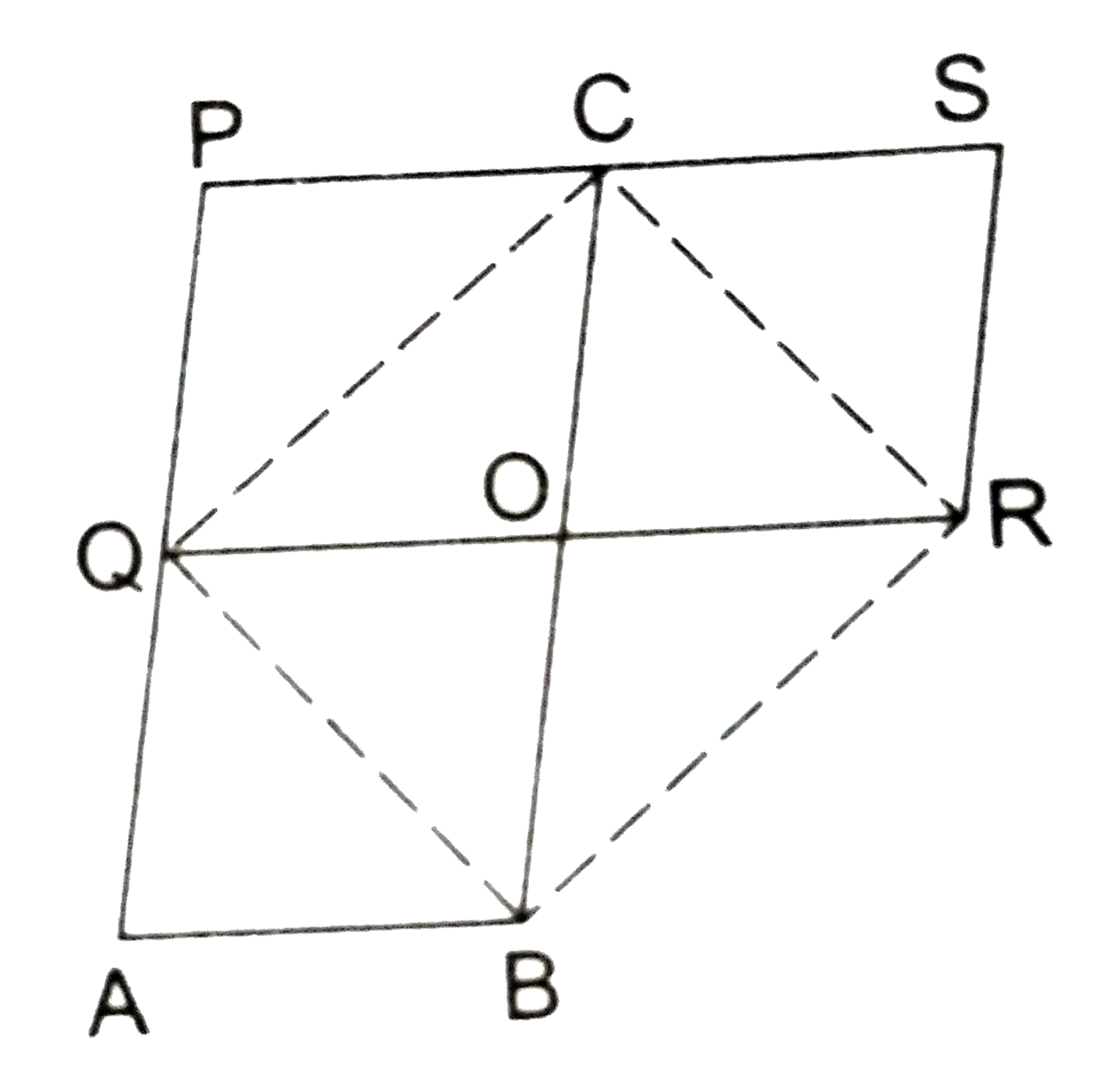
In the adjoining figure, PQRS is a parallelogram. A and B are the mid-points of PQ of SR respectively. If PS= BR, then prove that quadrilateral ADBC is a reactangle.
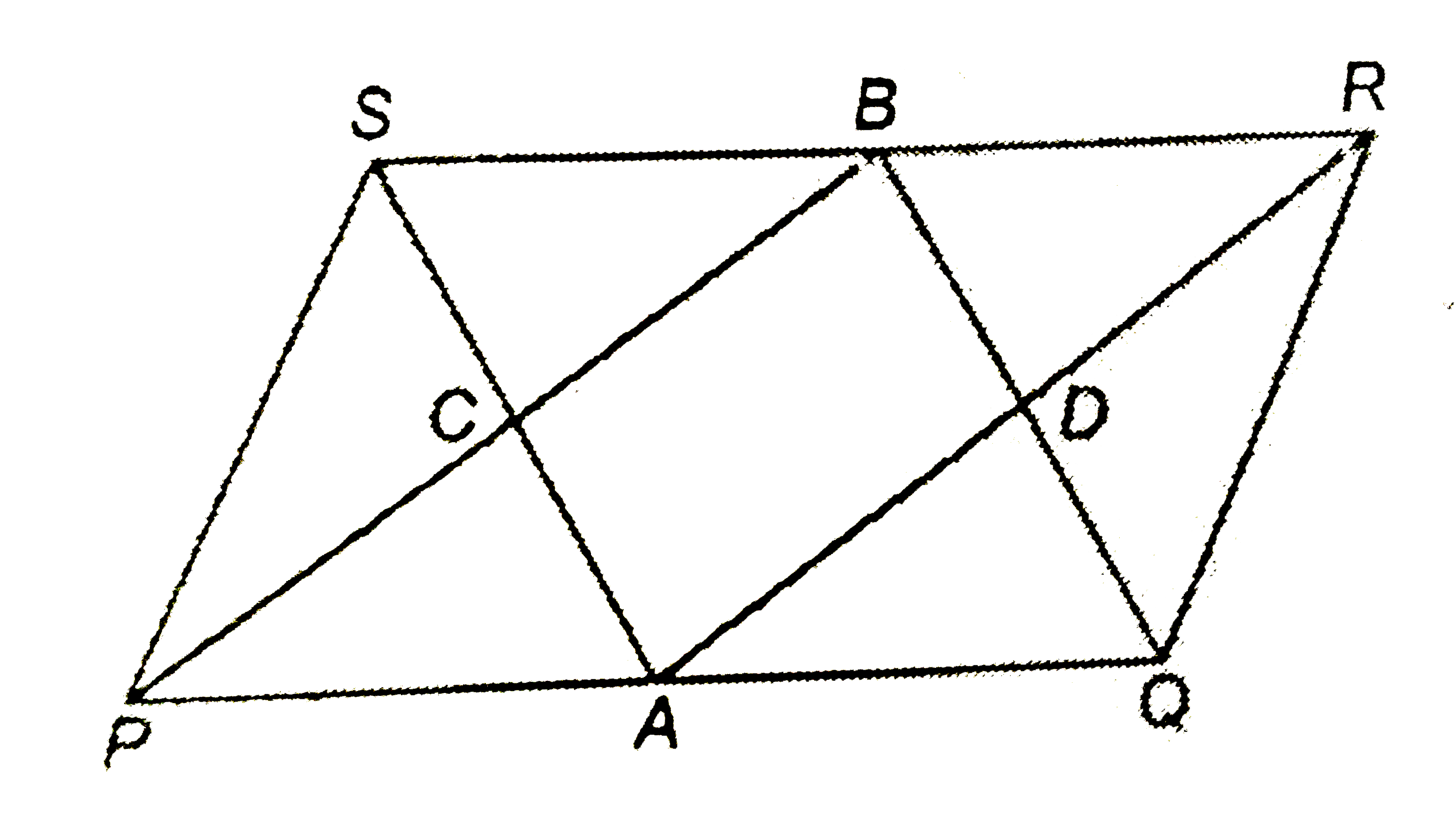
Since is a parallelogram
Now since
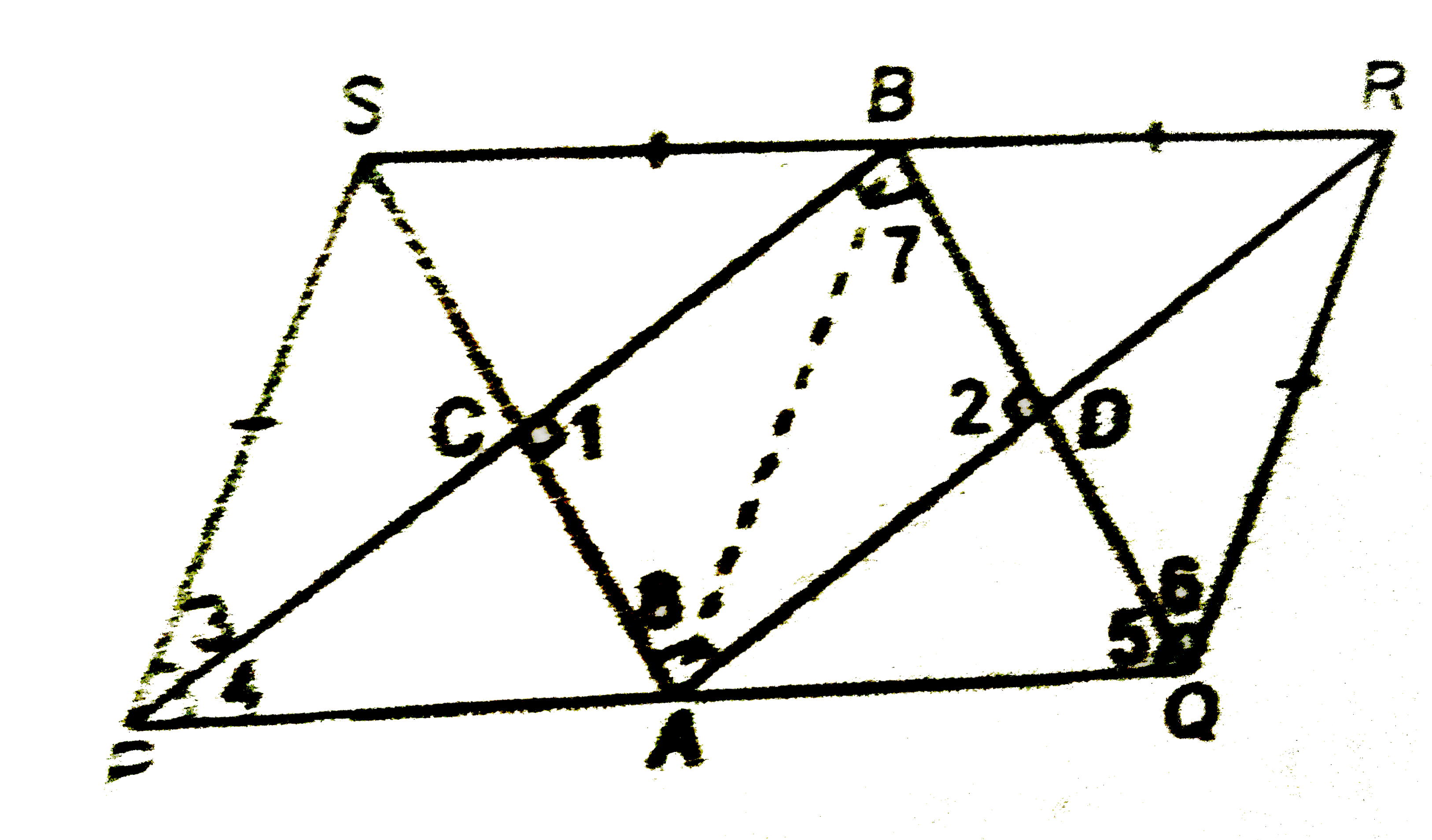
From (1) and (2), we get
is a parallelogram
But since PA = PS = SB
is a rhombus.
Similarly is a rhombus
Now, we know that diagongal PB bisects bisects
(we can prove easily by proving coagruent)
Now, in
Each of the 4 angle of a quadrilateral ABCD is
So, is a reactangle.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Problems From NCERT/exemplar
11 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise
10 Videos
Similar Questions
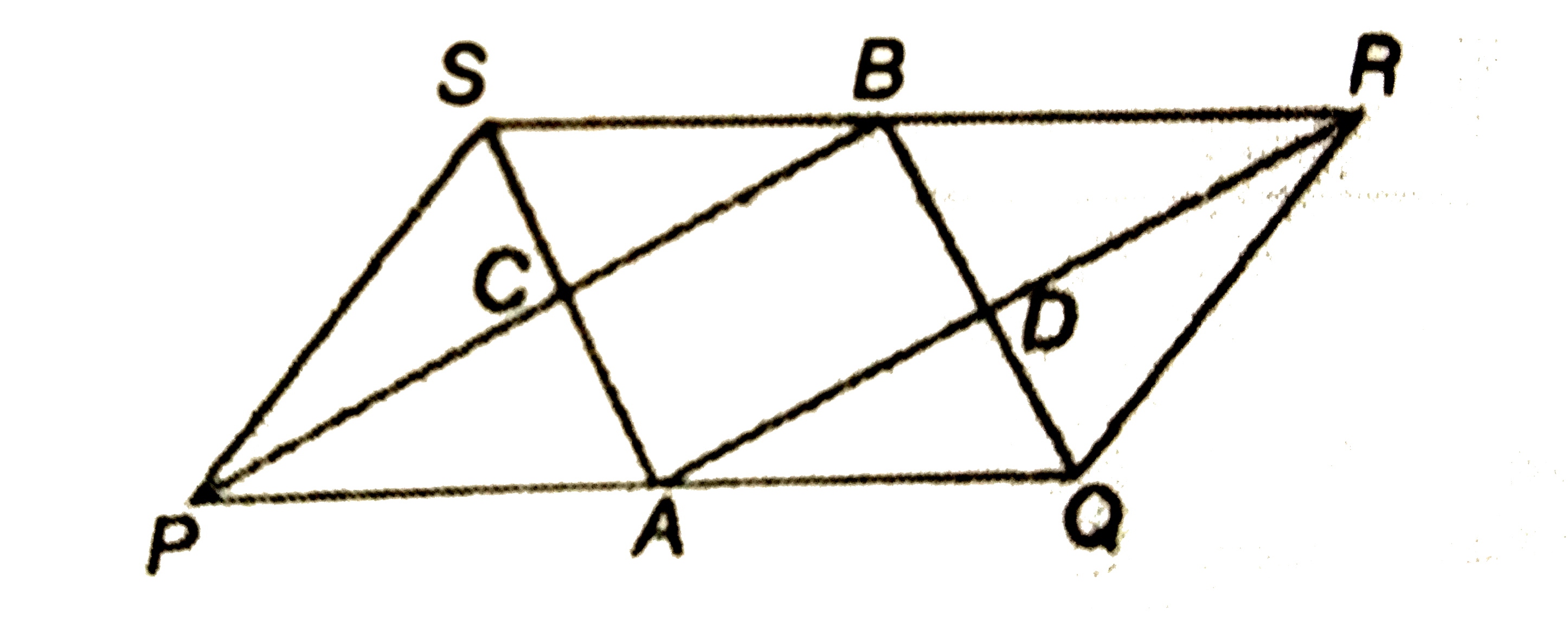
In the given figure, PQRS is a parallelogram. A and B are the mid-point of ¯¯¯¯¯¯PQ and ¯¯¯¯¯SR respectively. If PS=BR, then the quadrilateral ADBC is a…………………… ,
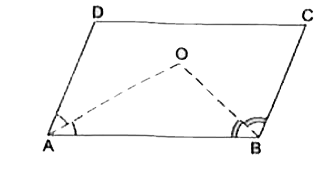
View SolutionIn the adjoining figure, ABCD is a parallelogram , AO and BO are the bisectors of ∠A and ∠B respectively. Prove that ∠AOB=90∘.
View Solution
Knowledge Check
In the given figure, PQRSis a parallelogram and U is the mid point of QR. If PQ=4cm, then what is the value of PT (in cm.)?
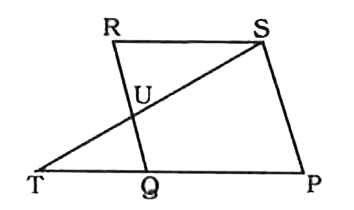 A6B6.5C7.5D8
A6B6.5C7.5D8Let □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
A3¯¯¯¯¯¯¯¯MNB4¯¯¯¯¯¯¯¯MNC2¯¯¯¯¯¯¯¯MND2¯¯¯¯¯¯¯¯NM
□PQRS is a reactangle. If A, B and C are the mid-points of PQ, PS and QR respectively, then prove that
AB+AC=12(PR+SQ).
View SolutionIn the adjoining figure, PQ=PR. Show that PS>PQ.
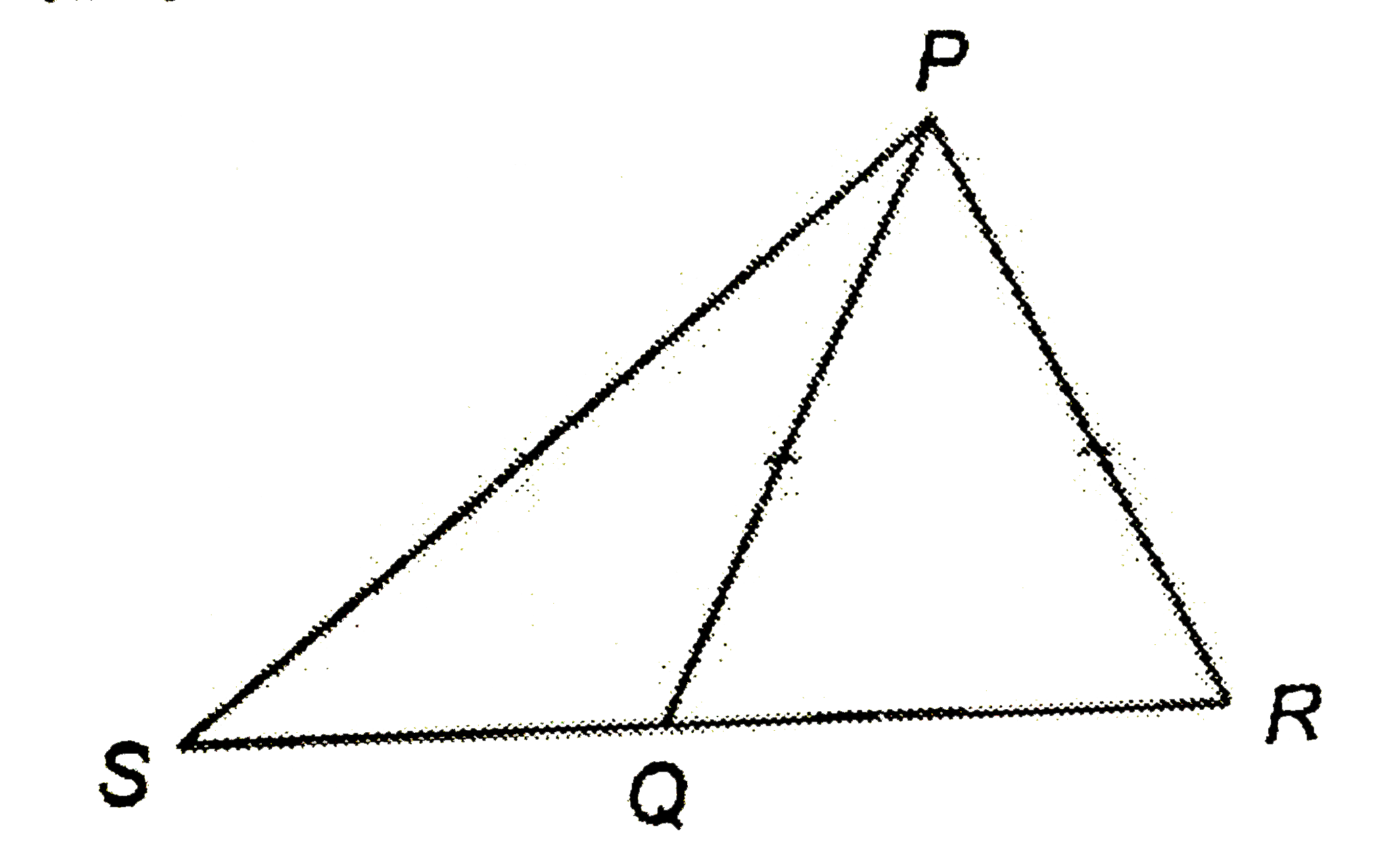
View SolutionIn the given figures, if PQRS is a parallelogram and AB||PS, then prove that OC||SR.
View SolutionIn the given figure, PQRS is a parallelogram. If X and Y are mid-point of PQ and SR respectively and diagonal SQ is joined. Find the ratio of area of (∣∣gmXQRY): area (ΔQSR)
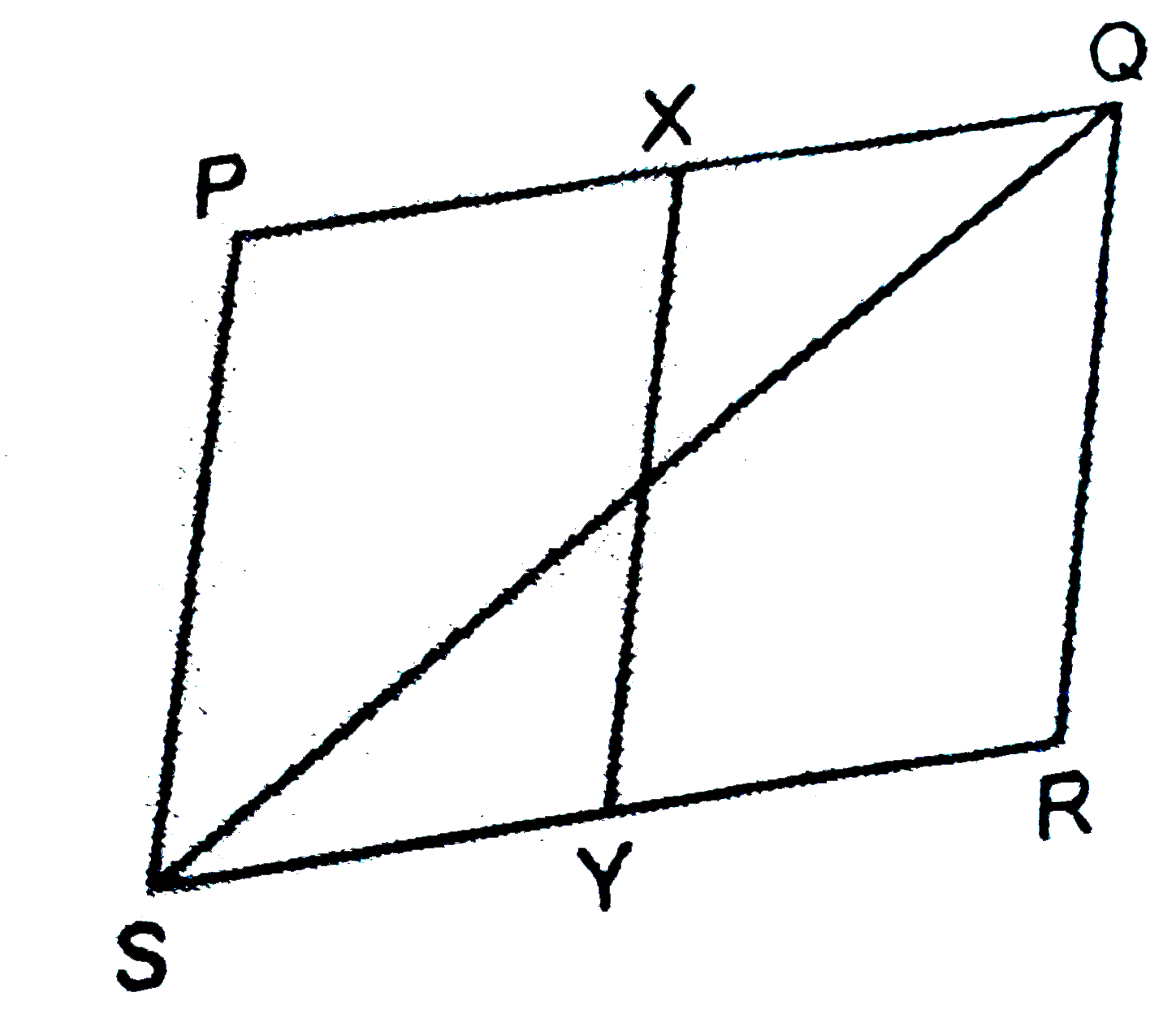
View SolutionIn the figure given below if PQRS is a parallelogram and AB |PS then prove that OC ||SR.
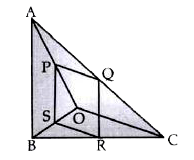
View SolutionIn the adjoining figure, PQRS and PABC are two parallelogram of equal area. Prove that QC||BR.
View Solution
