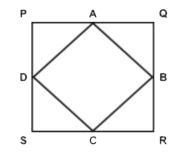
is a rectangle. Points A, B, C and D are the mid points of sides respectively. If area of is , then what is the area (in cm) of ?
24
6
16
12
The correct Answer is:A
To find the area of triangle BCD in rectangle PQRS, we can follow these steps:
Step 1: Understand the Geometry
We have a rectangle PQRS, where points A, B, C, and D are the midpoints of sides PQ, QR, RS, and PS, respectively.
Step 2: Find the Area of Rectangle PQRS
Given that the area of triangle PQR is 48 cm², we know that triangle PQR is half of the rectangle PQRS because the diagonal PR divides the rectangle into two equal triangles.
Area of rectangle PQRS=2×Area of triangle PQR=2×48 cm2=96 cm2
Step 3: Determine the Area of Quadrilateral DBRS
Since A, B, C, and D are midpoints, quadrilateral DBRS is half of the rectangle PQRS. Therefore, the area of quadrilateral DBRS is:
Area of DBRS=12×Area of rectangle PQRS=12×96 cm2=48 cm2
Step 4: Relate Triangle BCD to Quadrilateral DBRS
Triangle BCD is formed within quadrilateral DBRS. Since BD is parallel to RS and both triangles share the same base BD and height from point C to line RS, we can use the property of triangles in parallel lines.
Step 5: Calculate the Area of Triangle BCD
The area of triangle BCD is half of the area of quadrilateral DBRS:
Area of triangle BCD=12×Area of DBRS=12×48 cm2=24 cm2
Final Answer
The area of triangle BCD is 24 cm².
---
We have a rectangle PQRS, where points A, B, C, and D are the midpoints of sides PQ, QR, RS, and PS, respectively.
Given that the area of triangle PQR is 48 cm², we know that triangle PQR is half of the rectangle PQRS because the diagonal PR divides the rectangle into two equal triangles.
Since A, B, C, and D are midpoints, quadrilateral DBRS is half of the rectangle PQRS. Therefore, the area of quadrilateral DBRS is:
Triangle BCD is formed within quadrilateral DBRS. Since BD is parallel to RS and both triangles share the same base BD and height from point C to line RS, we can use the property of triangles in parallel lines.
The area of triangle BCD is half of the area of quadrilateral DBRS:
The area of triangle BCD is 24 cm².
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-VII)
Explore 6 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-VIII)
Explore 27 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-V)
Explore 30 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
□PQRS is a reactangle. If A, B and C are the mid-points of PQ, PS and QR respectively, then prove that
AB+AC=12(PR+SQ).
View SolutionIn the given figure , PQR is an equilateral triangle with side as 12 cm . S and T are the mid points of the sides PQ and PR respectively . What ist he area (in cm2) of the shaded region ?
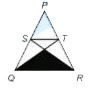
View Solution
Knowledge Check
PQRS is a rectangle, A, B, C and D are the mid points of sides PQ, QR, RS and PS respectively. If area of ΔPQR is 48 cm2, then what is the area (in cm2) of ΔBCD?
A24B6C16D12PQRS is a square with side 10 cm. A, B, C and D are mid-points of PQ, QR, RS and SP respectively. Then the perimeter of the square ABCD so formed is
A10√2cmB20√2cmC25√2cmD15√2cmLet □PQRS be a quadrilateral. If M and N are the mid-points of the sides PQ and RS respectively, then PS+QR=
A3¯¯¯¯¯¯¯¯MNB4¯¯¯¯¯¯¯¯MNC2¯¯¯¯¯¯¯¯MND2¯¯¯¯¯¯¯¯NM
In the given figure L, M and N are mid point of the sides PQ, PR and QR respectively of ΔPQR. If PQ = 4.4 cm, QR = 5.6 cm and PR = 4.8 cm then find the perimeter of ΔLMN.
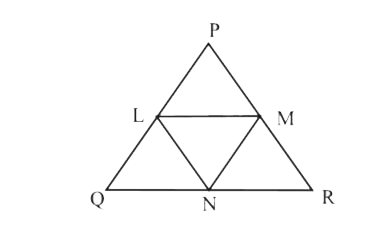
View SolutionIn ΔPQR, a line parallel to side QR cuts the side PQ and PR at points M and N respectively and point M divide PQ in the ratio of 1 : 2. If area of ΔPQR is 360 cm2, then what is the area (in cm2) of quadrilateral MNRQ?
View SolutionPoints A, B, C and D are midpoints of the sides of square PQRS. If the area of PQRS is 36 Sqcm, the area of ABCD is ...........Sqcm
View SolutionThe triangle is formed by joining the mid point of the sides AB, BC and CA of ΔABC and the area of ΔPQR is 6cm2, then the area of ΔABC is :
View SolutionIf D is the mid-point of the side BC of ΔABCand the area of ΔABD and the area of ΔACD is 16cm2, then the area of ΔABC is
View Solution