Q is a point in the interior of a rectangle ABCD. If QA=3cm,QB=4cmandQC=5cm, then the length of QD (in cm) is
3√2
5√2
√34
√41
The correct Answer is:A
To solve the problem, we will use the relationship that holds for a point Q inside rectangle ABCD. The relationship states that:
QA2+QC2=QB2+QD2
Given:
- QA=3cm
- QB=4cm
- QC=5cm
We need to find QD.
1. Square the lengths of QA, QB, and QC:
QA2=32=9
QB2=42=16
QC2=52=25
2. Substitute the squared values into the relationship:
QA2+QC2=QB2+QD2
Substitute the values we calculated:
9+25=16+QD2
3. Combine the left side:
34=16+QD2
4. Isolate QD2:
QD2=34−16
QD2=18
5. Take the square root to find QD:
QD=√18=√9×2=3√2cm
Final Answer:
The length of QD is 3√2cm.
---
- QA=3cm
- QB=4cm
- QC=5cm
QA2=32=9
QB2=42=16
QC2=52=25
QA2+QC2=QB2+QD2
Substitute the values we calculated:
9+25=16+QD2
34=16+QD2
QD2=34−16
QD2=18
QD=√18=√9×2=3√2cm
The length of QD is 3√2cm.
Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-VII)
Explore 6 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-VIII)
Explore 27 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-V)
Explore 30 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
Q is a point interior of a rectangle ABCD . If QA=3cm,QB=4cm and QC=5cm,then length of QD is
View SolutionO is any point inside a rectangle ABCD. Prove that OB2+OD2=OA2+OC2.
DEDUCTION In the given figure, O is a point inside a rectangle ABCD such that OB=6cm,OD=8cmandOA=5cm, find the length of OC.
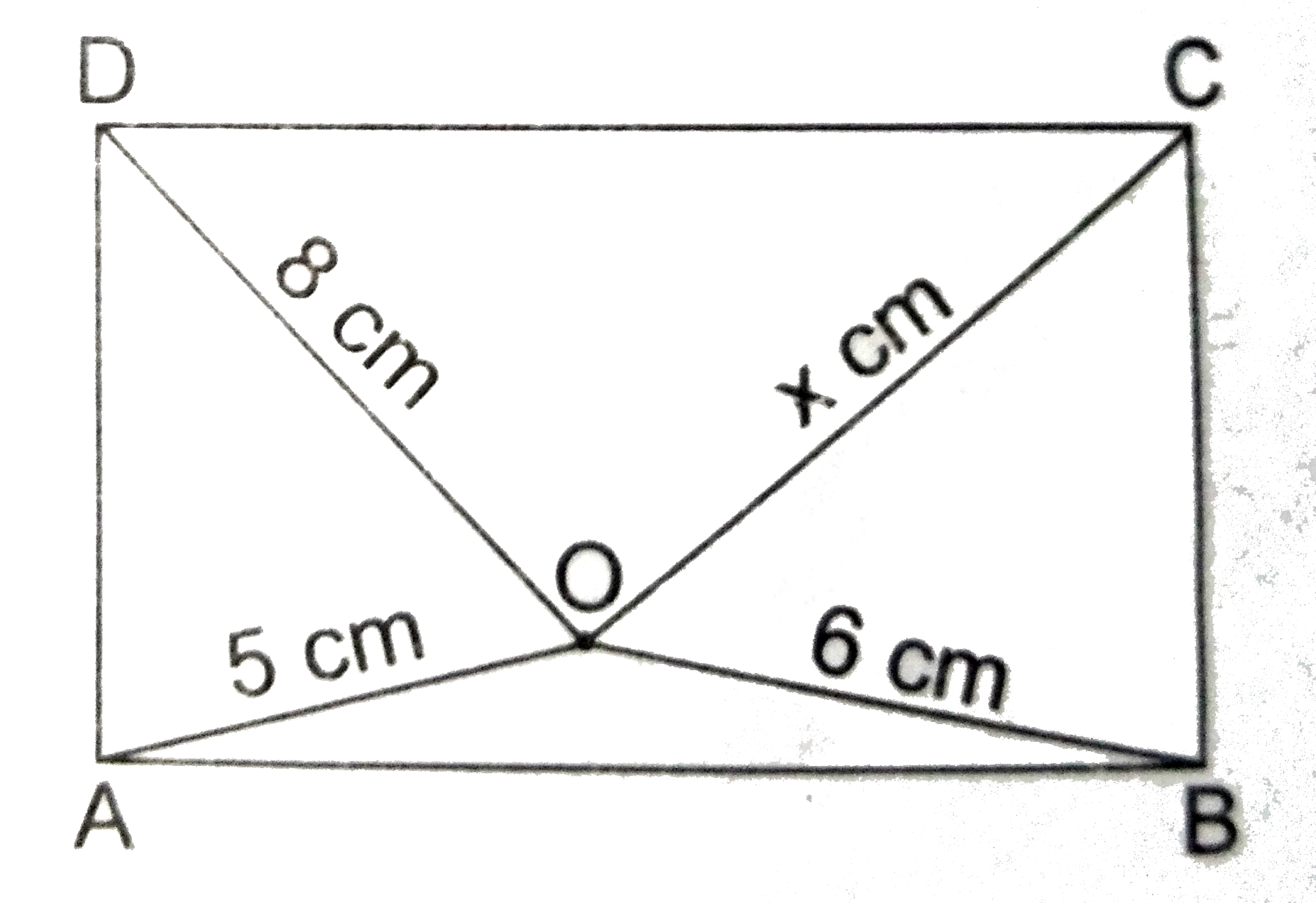
View Solution
Knowledge Check
Length of the perpendiculars from a point in the interior of an equilateral triangle on its sides are 3 cm, 4 cm and 5 cm. Area of the triangle is
A48√3cm2B54√3cm2C72√3cm2D80√3cm2P is an interior point of quadrilateral ABCD and AB=3.5cm, BC=4cm,CD=4.8cm and AD=3.7 cm . Then which of the following can be the possible value of (AP+BP+CP+DP) ?
A7.9 cmB8 cmC8.1 cmD6.4 cm
Construct a rectangle ABCD whose sides AB=5.4 cm and BC=4.5cm.
View SolutionABCD is a trapezium in which AB || DCand P, Qare points on AD and BC respectively, such that PQ II DC. If PD - 18 cm, BQ = 35 cm and QC = 15 cm, then find the length of AD.
View SolutionP and Q are points on the sides AB and AC respectively of a △ABC. If AP= 2cm, PB = 4cm AQ= 3cm and QC= 6cm. Show that BC= 3PQ.
View SolutionO is a point situated inside a rectangle ABCD. If sides OA, OC and OD are 6 cm, 8 cm and 6 cm respectively, then find the value of OB-
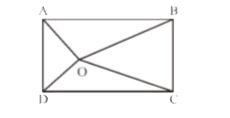
View Solutionin the figure, X is a point in the interior of square ABCD.AXYZ is also a square. If DY=3cmandAZ=2cm. Then BY=
View SolutionIf the perimeter of a rectangle is 10 cm and the area is 4cm2, then its length is
View Solution
