If a particle is moving the velocity v(t)=cos πt, along a straight line such that at t=0, s=4, its position function is given by
1πcosπt+2
−1πsinπt+4
1πsinπt+4
none of these
The correct Answer is:C
Step by step video, text & image solution for If a particle is moving the velocity v(t)=cos pit, along a straight line such that at t=0, s=4, its position function is given by by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the position function of a particle that moves with velocity v(t)=cosπt along a coordinate line, assuming that the particle has coordinate s=4 or time t=0.
View SolutionA particle moves with a velocity v(t)=(12)kt2 along a straight line . Find the average speed of the particle in a time t.
View Solution
Knowledge Check
The figure shows a velocity-time graph of a particle moving along a straight line
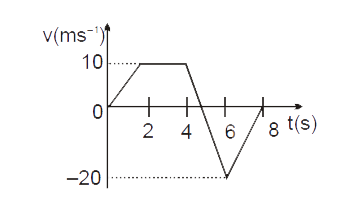
If the particle starts from the position x0=–15 m, then its position at t = 2s will beA−5mB5mC10 mD15 mThe figure shows a velocity-time graph of a particle moving along a straight line
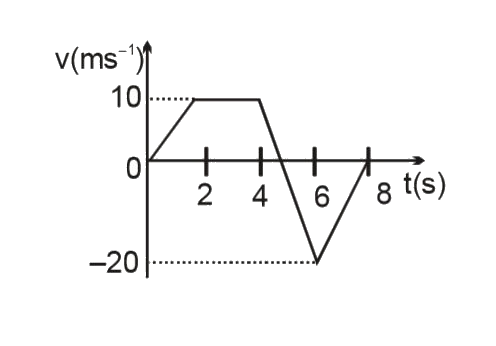
Q. If the particle starts from the position x0 = –15 m, then its position at t = 2s will beA−5mB5mC10mD15mThe figure shows a velocity-time graph of a particle moving along a straight line
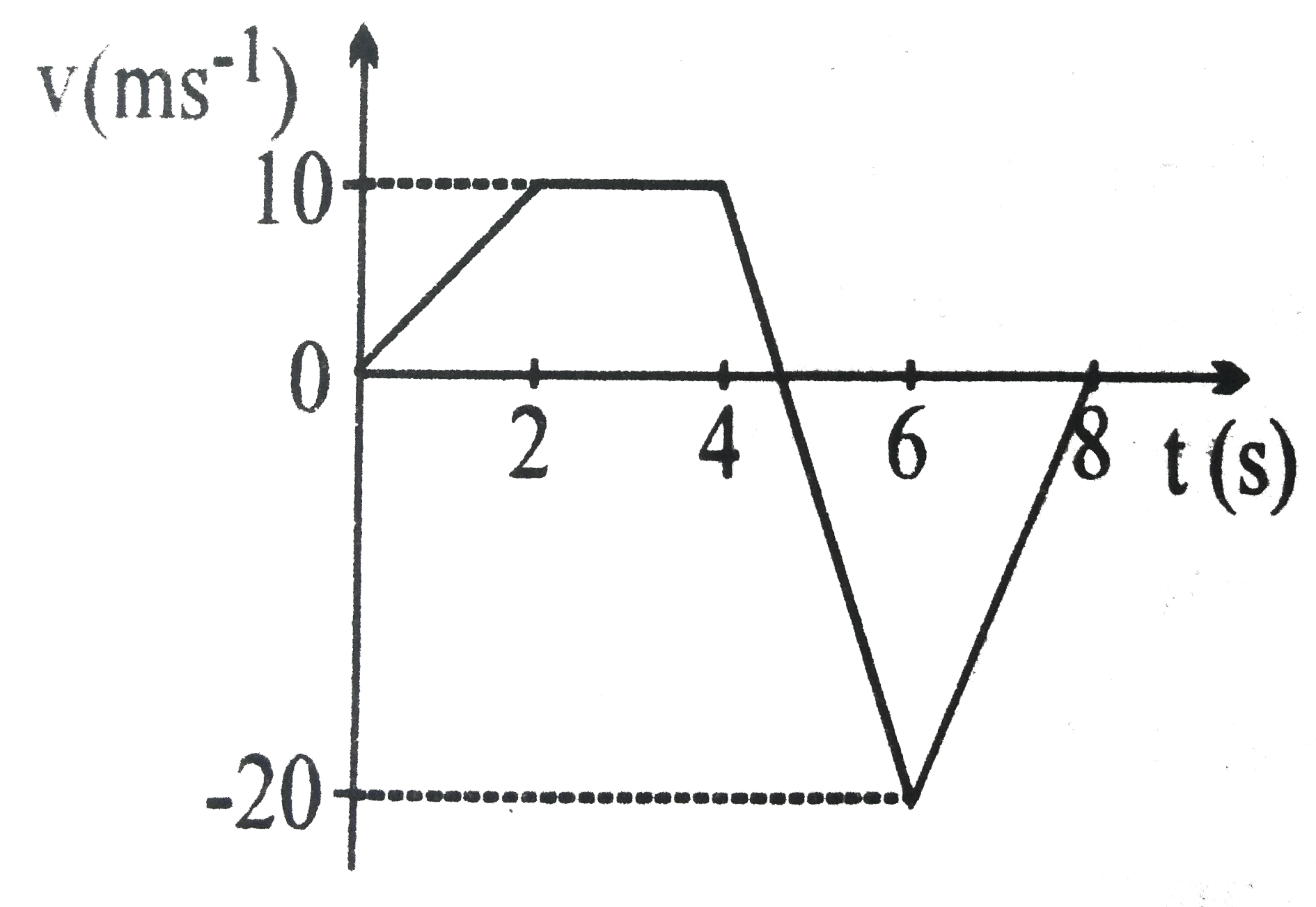
If the particles starts form the position x0=−15m, then its position at t=2s will beA−5B5mC10mD15m
A particle move with a velocity v=αt3 along a straight line.The average velocity in time interval t=0 to t=T is
View Solutiona particle is moving in a straight line such that its velocity varies is given by v=10−2t, where v isin the first 8 second.
View SolutionA particle in moving in a straight line such that its velocity is given by v=12t−3t2, where v is in m//s and t is in seconds. If at =0, the particle is at the origin, find the velocity at t=3s.
View SolutionFind the average velocity of a particle moving along a straight line such that its velocity changes with time as v(m/s)=4sin.π2t, over the time interval t=0 to t=(2n−1)2 seconds. (n being any + ve integer).
View SolutionA particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
View Solution