Find the average velocity of a particle moving along a straight line such that its velocity changes with time as v(m/s)=4sin.π2t, over the time interval t=0 to t=(2n−1)2 seconds. (n being any + ve integer).
Displacement over the interval t=0 to t=2(2n−1)s
s=42(2n−1)∫0sin(π2t)dt
=−8π[cos(π2t)]2(2n−1)0=16πm
∴ Average velocity =162(2n−1)π=8(2n−1)πm/s
Topper's Solved these Questions
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Problem
Explore 14 Videos
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Problems and Practice
Explore 16 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Comprehension type
Explore 11 Videos
- MOTION IN TWO AND THREE DIMENSIONSBook:GRB PUBLICATIONChapter:MOTION IN TWO AND THREE DIMENSIONSExercise:All Questions
Explore 210 Videos
Similar Questions
If velocity of a partical moving along a straight line changes sinusoidally with time as shown in given graph. Find the average speed over time interval t=0 to t=2(2n−1) second, n being any positive interget.
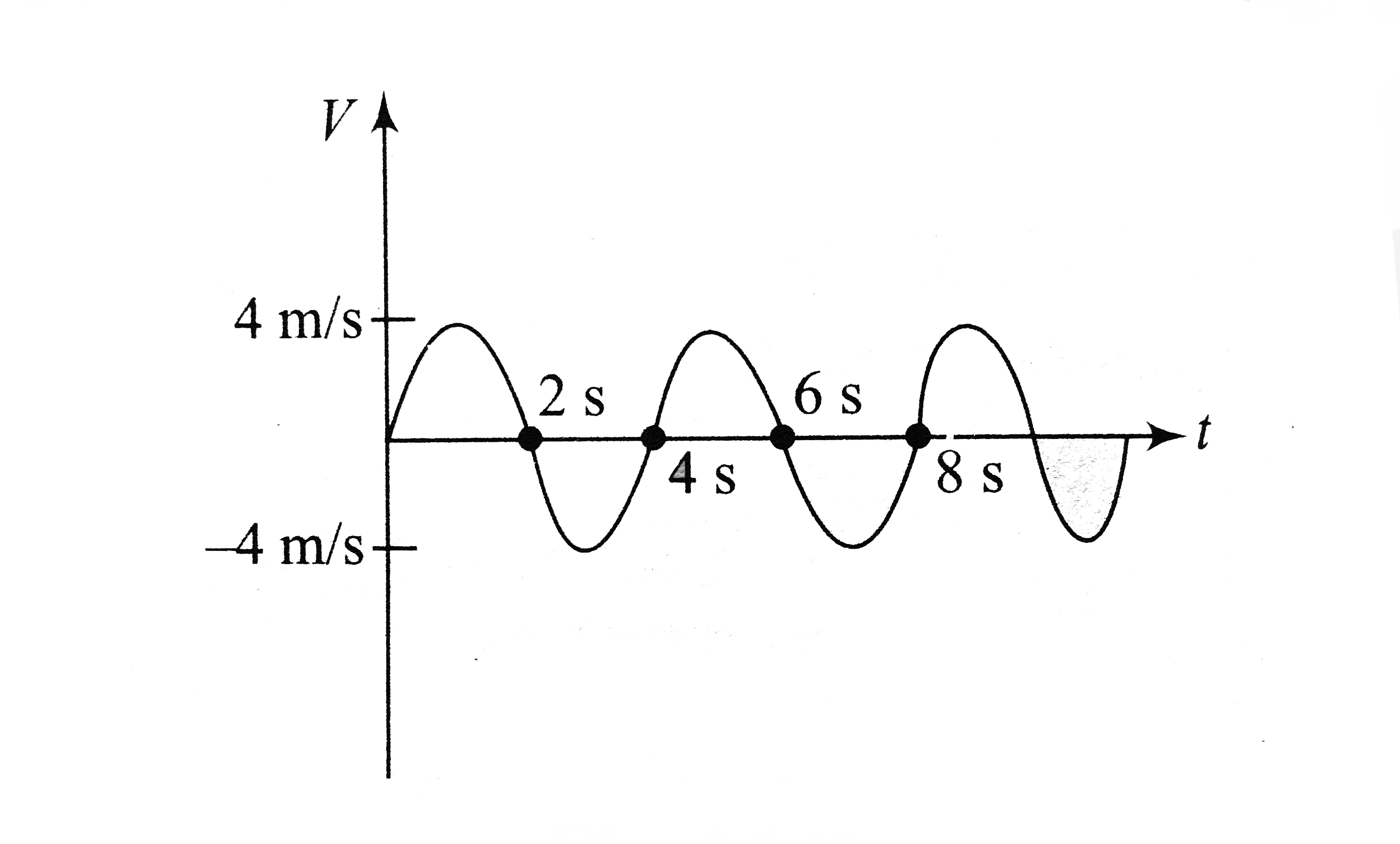
View SolutionA particle moves along a staight line such that its displacement at any time t is given by s=t3−6t2+3t+4m. Find the velocity when the acceleration is 0.
View Solution
Knowledge Check
A particle moves along a straight line its velocity dipends on time as v=4t−t2. Then for first 5s:
AAverage velcotu is 25/3ms−1BAverage speed is 10ms−1.CAverage velcotu is 5/3ms−1DAcceleration is 4ms−2 at t=oVelocity of a particle moving along a straight line at any time 't' is give by V=cos(π3t) . Then the distance travelled by the particle in the first two seconds is :
A3π[2−√32]B[2−√32]C2π[2−√32]D4π[2−√32]A particle is moving on a straight line. Its velocity at time t is (8−2t)m/s. What is the total distance covered from t=0 to t=6s?
A12mB16mC18mD20m
The acceleration of a particle moving along a straight line is (6t2−3t) cm/s2, at time t seconds, If the velocity of the particle at time 2 seconds be 10 cm/s,find its veloctiy at time t seconds.
View SolutionFor which of the following graphs the average velocity of a particl moving along a straight line for time interval (0,t) must be negative−
View SolutionA particle moves along a straight line such that its displacement at any time t is given by s=3t3+7t2+14t+5. The acceleration of the particle at t=1s is
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The distance travelled by particle from t=0 to t=2seconds is :
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The displacement of aprticle from t=0 to t=2 seconds is :
View Solution

