A particle moves with a velocity v(t)=(12)kt2 along a straight line . Find the average speed of the particle in a time t.
To find the average speed of a particle moving with a velocity given by v(t)=12kt2 over a time interval from 0 to t, we will follow these steps:
Step 1: Understand the formula for average speed
The average speed vavg is defined as the total distance traveled divided by the total time taken. Mathematically, it can be expressed as:
vavg=Total DistanceTotal Time
Step 2: Express the distance traveled in terms of velocity
The distance s traveled by the particle can be found by integrating the velocity function over the time interval from 0 to t:
s=∫t0v(t)dt
Substituting the expression for v(t):
s=∫t012kt2dt
Step 3: Perform the integration
Now, we will compute the integral:
s=12k∫t0t2dt
The integral of t2 is:
∫t2dt=t33
Thus, we have:
s=12k(t33)t0=12k⋅t33=kt36
Step 4: Calculate the average speed
Now that we have the total distance traveled, we can find the average speed:
vavg=st=kt36t
This simplifies to:
vavg=kt26
Final Answer
The average speed of the particle over the time interval t is:
vavg=kt26
---
The average speed vavg is defined as the total distance traveled divided by the total time taken. Mathematically, it can be expressed as:
vavg=Total DistanceTotal Time
The distance s traveled by the particle can be found by integrating the velocity function over the time interval from 0 to t:
s=∫t0v(t)dt
Substituting the expression for v(t):
s=∫t012kt2dt
Now, we will compute the integral:
s=12k∫t0t2dt
The integral of t2 is:
∫t2dt=t33
Thus, we have:
s=12k(t33)t0=12k⋅t33=kt36
Now that we have the total distance traveled, we can find the average speed:
vavg=st=kt36t
This simplifies to:
vavg=kt26
The average speed of the particle over the time interval t is:
vavg=kt26
Topper's Solved these Questions
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:Problem (subjective)
Explore 10 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:Problem (objective)
Explore 14 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:NUMERICAL BASES QUESTIONS
Explore 1 Video
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
Similar Questions
Knowledge Check
A particle move with velocity v1 for time t1andv2 for time t2 along a straight line. The magntidue of its average acceleration is
Av2−v1t1−t2Bv2−v1t1+t2Cv2−t1t2−t1Dv1+v2t1−t2A particle moves from A to B with a uniform velocity v1 and from B to A with a velocity v2. If it moves along a straight line between A and B, then the average velocity of the particle is
Av1v22Bv1+v22C2v1v2v1+v2DzeroThe velocity of a particle varies with time as →v=3ˆi+(4−5t)ˆjms−1. Find the average velocity of the particle for a time interval between t=0 and a time when the speed of the particle becomes minimum.
A(3ˆi+2ˆj)ms−1B(6ˆi+5ˆj)ms−1C(4ˆi+ˆj)ms−1D(3ˆi−5ˆj)ms−1
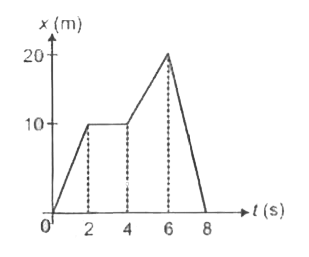
The position (x) - time (t) graph for a particle moving along a straight line is shown in figure. The average speed of particle in time interval t = 0 to t = 8 s is
View SolutionThe acceleration of a particle moving along a straight line at any time t is given by a = 4 - 2v, where v is the speed of particle at any time t The maximum velocity is
View SolutionVelocity time graph for the motion of a particle along a straight line is as shown in figure.

Average speed of the particle for the whole motion is:
View SolutionIf a particle is moving the velocity v(t)=cos πt, along a straight line such that at t=0, s=4, its position function is given by
View SolutionForce acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View Solution

