The statement (p⇒q)⇔(~p∧q) is a
A
tautology
B
contradiction
C
Neither (a) nor (b)
D
None of these
Video Solution
Text Solution
The correct Answer is:C
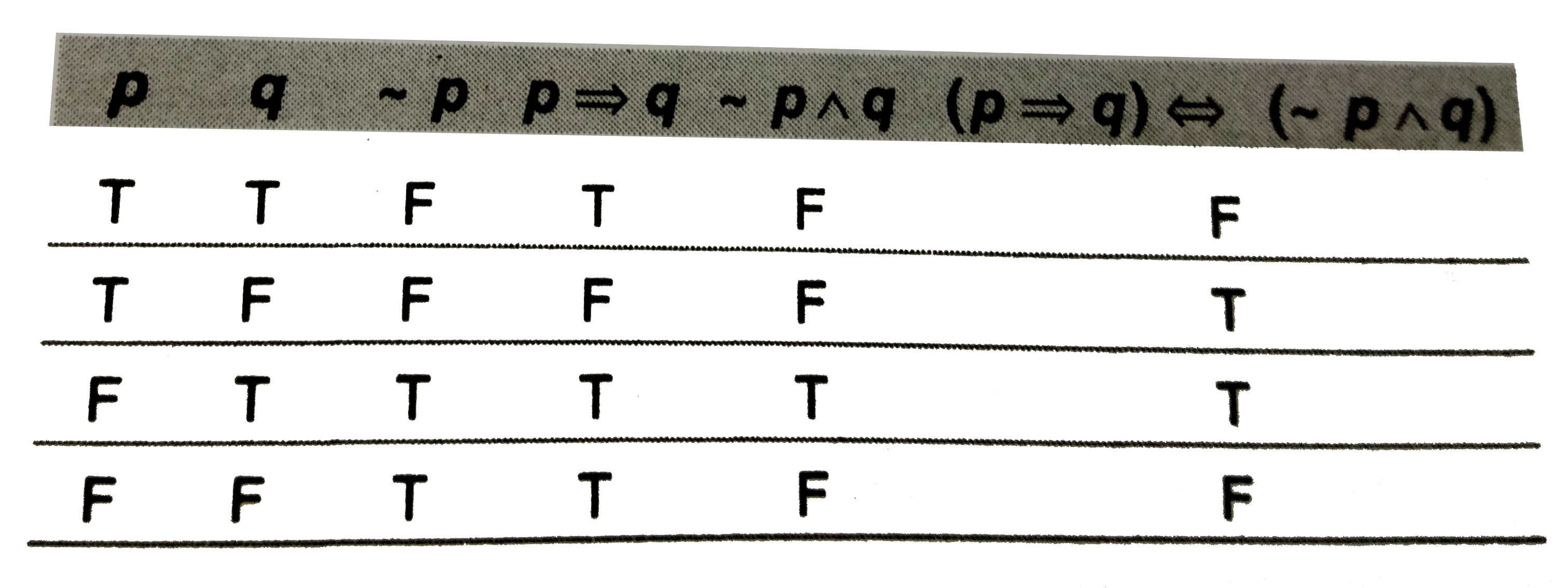
Hence, (p⇒q)⇔(~p∧q) is neither a tautology nor, contradiction.
|
Topper's Solved these Questions
- MATHEMATICAL LOGIC Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:MATHEMATICAL LOGIC Exercise:PRACTICE EXERCISE (Exercies 2 (MISCELLANEOUS PROBLEMS))
Explore 26 Videos
- MATHEMATICAL LOGIC Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:MATHEMATICAL LOGIC Exercise:MHT CET CORNER
Explore 22 Videos
- Linear Programming Book:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:Linear Programming Exercise:MHT CET Corner
Explore 13 Videos
- MATRICESBook:MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSChapter:MATRICESExercise:MHT CET CORNER
Explore 18 Videos
Similar Questions
Knowledge Check
Statement-1 : (p∧~q)∧(~p∧q) is a facllocy.
Statement -2: (p→q)↔(~q→~p) is a tautology .AStatement-1 is true, statement-2 is true, statement-2 is correct explanation for statement-1BStatement-1 is true, statement-2 is true, statement-2 is not a correct explanation for statement-1CStatement-1 is true, statement-2 is falseDStatement-1 is false. statement-2 is trueThe statement (p→~q)⇔(p∧q) is a-
ATautologyBcontradictionCNeither tautology nor contradictionDNoneFor any two statements p and q, the statement
~(p∧q)∨(~p∧q)
is equivalent toA~pBpCqDp ∧ q
If p and q are two statements, then (p⇒q)⇔(~q⇒~p) is
View SolutionThe proposition S:(p⇒q)⇔(~p∨q) is a
View SolutionIn the truth table for the statement (~p⇒~q)∧(~q⇒~p), the last column has the truth value in the following order
View SolutionLet p and q be two statements. Then, (~p∨q)∧(~p∧~q) is a
View SolutionThe statement (p → q) ∨ (q → p) is
View Solution

