The statement (p→~p)∧(~p→p) is
A
tautology
B
contradiction
C
tautology and contradiction
D
Neither tautology nor contradiction
Video Solution
Text Solution
The correct Answer is:B
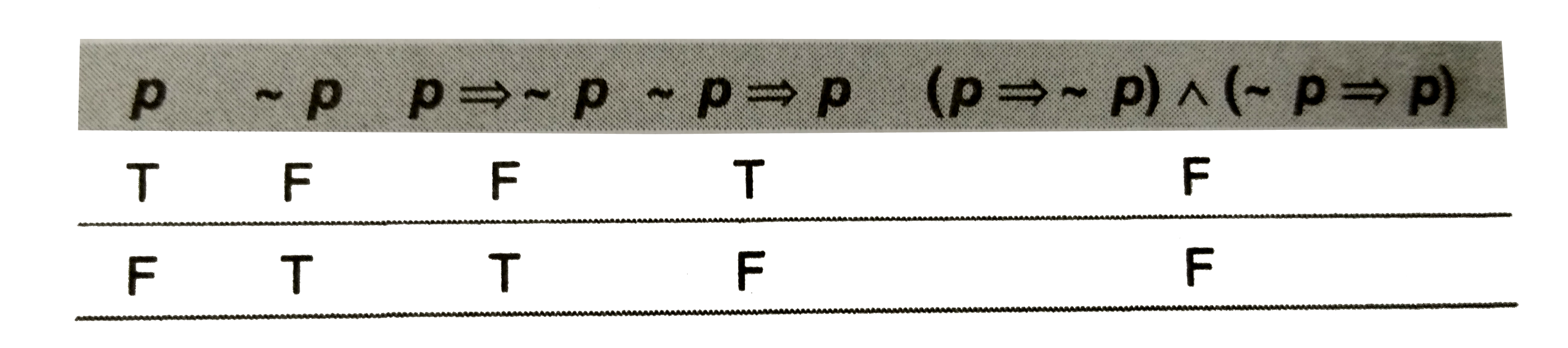
Clearly, (p⇒~p)∧(~p⇒p) is a contradiction.
|
Topper's Solved these Questions
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - PRACTICE EXERCISE (Exercies 2 (MISCELLANEOUS PROBLEMS))
26 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner
13 Videos
- MATRICESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATRICESEXERCISE - MHT CET CORNER
18 Videos
Similar Questions
Knowledge Check
The statement (p⇒p)∧(~p⇒p) is a-
ATautology and contradictionBNeither tautology nor contradicationCContradictionDTautologyThe dual of the statement [p∨(~q)]∧(~p) is
Ap∨(~q)∨~pB(p∧~q)∨~pCp∧~(q∨~p)DNone of theseThe statement (p⇒q)⇔(~p∧q) is a
AtautologyBcontradictionCNeither (a) nor (b)DNone of these
