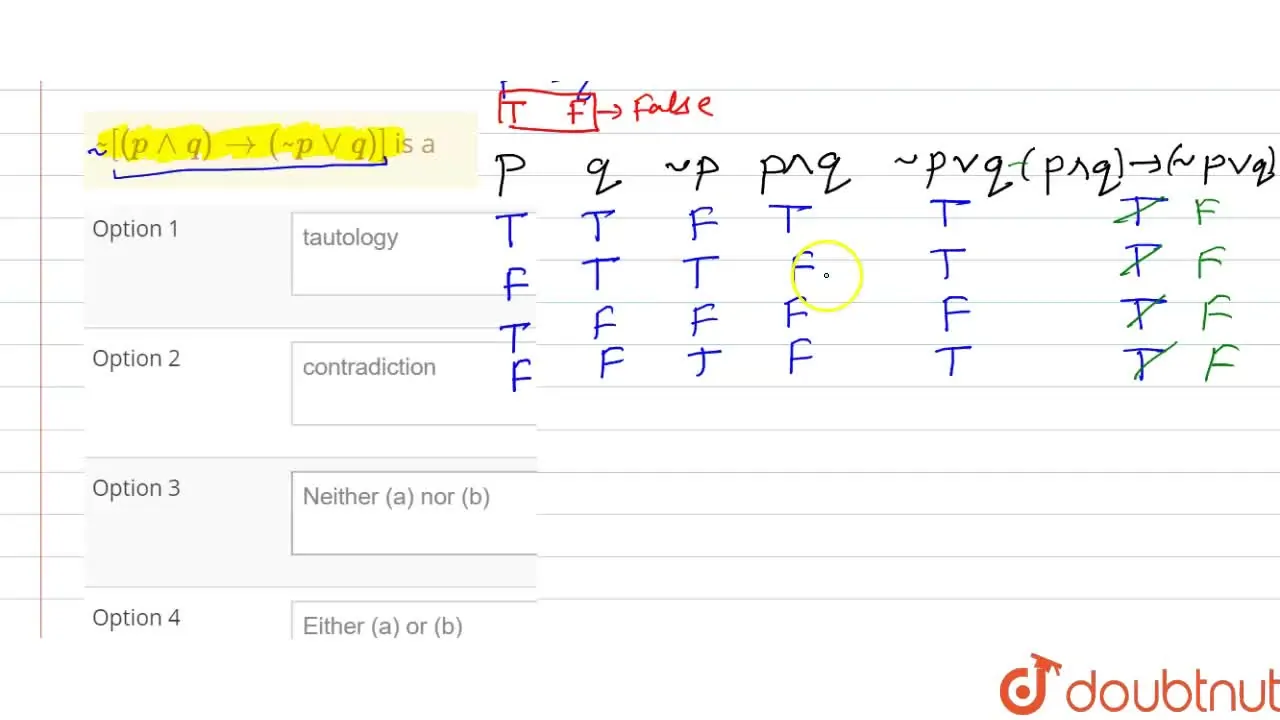
~[(p∧q)→(~p∨q)] is a
A
tautology
B
contradiction
C
Neither (a) nor (b)
D
Either (a) or (b)
Video Solution
Text Solution
The correct Answer is:B

It is clear from the table that,
~[(p∧q)→(~p∨q)] is a contradiction.
|
Updated on:21/07/2023
Related Playlists
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - PRACTICE EXERCISE (Exercies 2 (MISCELLANEOUS PROBLEMS))26videos
MATHEMATICAL LOGIC
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner13videos
Linear Programming
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATRICESEXERCISE - MHT CET CORNER18videos
MATRICES
Similar Questions
(p∧~q)∧(~p∨q) is
View SolutionNegation of (~p∧~q)∨(~p∨r) is
View SolutionThe proposition S:(p⇒q)⇔(~p∨q) is a
View SolutionThe property ~(p∧q)≡~p∨~q is called
View SolutionProve by constructing truth table that (p∧q)∧~(p∨q) is fallacy (contradiction)
View Solution~[p∨(~q)] is equal to-
View SolutionThe boolean expression ((p∧q)∨(p∨~q))∧(~p∨q) is equivalent to
View SolutionThe proposition ~(p∨~q)∨~(p∨q) is logically equivalent to
View SolutionShow that (p∧q)∨(~p)∨(p∧~q) is a tautology
View SolutionWrite 'T' for True and 'F' for False.
p∨(q∧r)≡(p∨q)∧(p∨r) is an associative law.View Solution