Show that (p∧q)∨(~p)∨(p∧~q) is a tautology
The correct Answer is: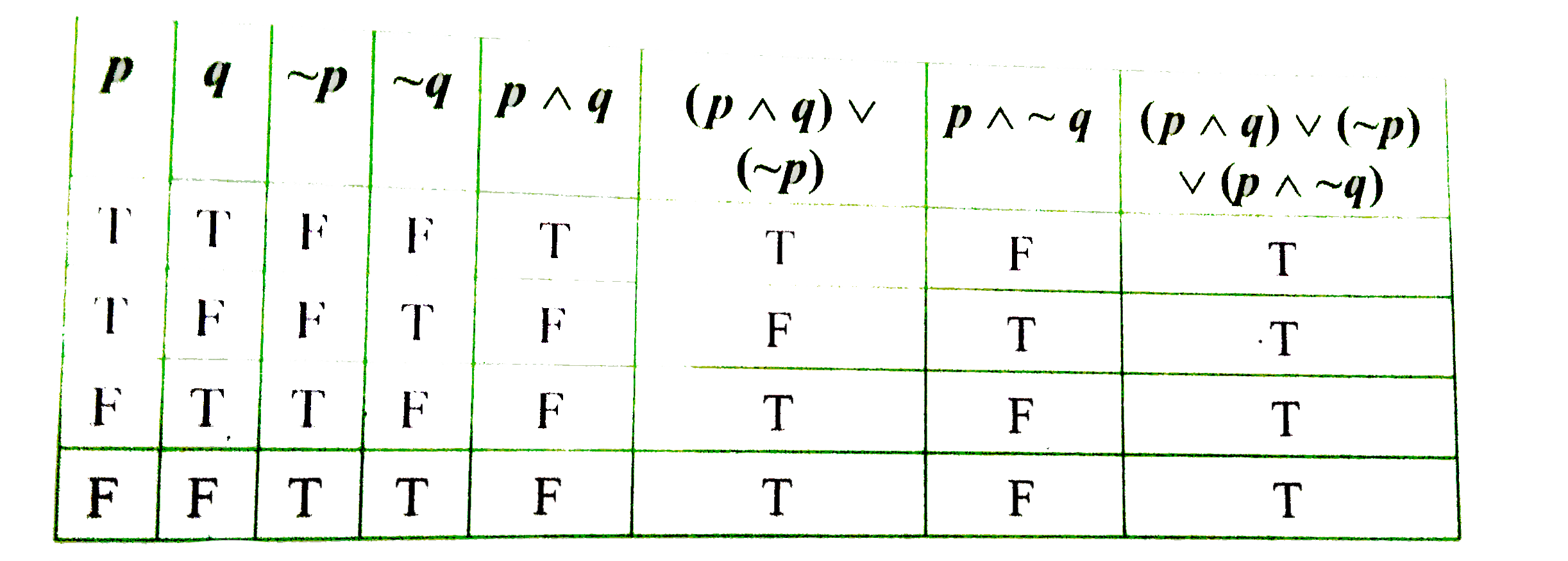
fol all possible truth values of p and q, the compound statement
(p∧q)∨(~p)∨(p∧~q) is true.
Thus, (p∧q)∨(~p)∨(p∧~q) is a tautology .
To show that the expression (p∧q)∨(¬p)∨(p∧¬q) is a tautology, we will create a truth table and evaluate the expression for all possible truth values of p and q.
Step 1: Identify the variables
The variables in the expression are p and q.
Step 2: Create a truth table
We will create a truth table that includes all possible combinations of truth values for p and q. There are 2 variables, so we will have 22=4 rows.
| p | q | ¬p | ¬q | p∧q | p∧¬q | (p∧q)∨(¬p)∨(p∧¬q) |
|-------|-------|------------|------------|----------------|---------------------|-----------------------------------------------------|
| T | T | F | F | T | F | T |
| T | F | F | T | F | T | T |
| F | T | T | F | F | F | T |
| F | F | T | T | F | F | T |
Step 3: Fill in the truth table
1. Negation of p (¬p): If p is True (T), then ¬p is False (F), and vice versa.
2. Negation of q (¬q): If q is True (T), then ¬q is False (F), and vice versa.
3. Conjunction p∧q: This is True only when both p and q are True.
4. Conjunction p∧¬q: This is True when p is True and q is False.
5. Final Expression: The final expression (p∧q)∨(¬p)∨(p∧¬q) is True if at least one of the components is True.
Step 4: Analyze the final column
From the truth table, we see that the final column, which represents the expression (p∧q)∨(¬p)∨(p∧¬q), is True for all combinations of p and q. Therefore, the expression is a tautology.
Conclusion
Since the expression evaluates to True for all possible truth values of p and q, we conclude that (p∧q)∨(¬p)∨(p∧¬q) is indeed a tautology.
The variables in the expression are p and q.
We will create a truth table that includes all possible combinations of truth values for p and q. There are 2 variables, so we will have 22=4 rows.
|-------|-------|------------|------------|----------------|---------------------|-----------------------------------------------------|
| T | T | F | F | T | F | T |
| T | F | F | T | F | T | T |
| F | T | T | F | F | F | T |
| F | F | T | T | F | F | T |
1. Negation of p (¬p): If p is True (T), then ¬p is False (F), and vice versa.
2. Negation of q (¬q): If q is True (T), then ¬q is False (F), and vice versa.
3. Conjunction p∧q: This is True only when both p and q are True.
4. Conjunction p∧¬q: This is True when p is True and q is False.
5. Final Expression: The final expression (p∧q)∨(¬p)∨(p∧¬q) is True if at least one of the components is True.
From the truth table, we see that the final column, which represents the expression (p∧q)∨(¬p)∨(p∧¬q), is True for all combinations of p and q. Therefore, the expression is a tautology.
Since the expression evaluates to True for all possible truth values of p and q, we conclude that (p∧q)∨(¬p)∨(p∧¬q) is indeed a tautology.
Topper's Solved these Questions
- MATHMETICAL REASONINGBook:CENGAGEChapter:MATHMETICAL REASONINGExercise:Exercise (Single)
Explore 38 Videos
- MATHMETICAL REASONINGBook:CENGAGEChapter:MATHMETICAL REASONINGExercise:JEE Previous Year
Explore 10 Videos
- MATHMETICAL REASONINGBook:CENGAGEChapter:MATHMETICAL REASONINGExercise:Exercise 10.1
Explore 8 Videos
- LOGARITHM AND ITS PROPERTIESBook:CENGAGEChapter:LOGARITHM AND ITS PROPERTIESExercise:JEE Previous Year
Explore 5 Videos
- MATRICESBook:CENGAGEChapter:MATRICESExercise:Solved Examples And Exercises
Explore 165 Videos
Similar Questions
Knowledge Check
~[(p∧q)→(~p∨q)] is a
AtautologyBcontradictionCNeither (a) nor (b)DEither (a) or (b)(p∧~q)∧(~p∨q) is
Aa contradictionBa tautologyCEither (a) or (b)DNeigher (a) nor (b)Given the following two statements
S1:(p∧:p)→(p∧q) is a tautology.
S2:(p∨:p)→(p∨q) is a fallacyAS1 is trueBS2 is trueCBoth S1 and S2 are trueDNone of these
Construct the switching circuit for each of the following statements :
(1) (p∧q)∨(~p)∨(p∧~q)
(2) (p∧q∧r)∨[~p∨(∧~r)]
(3) [p∨(~p∧q)]∨[(~q∧r)∨~p]
View SolutionWhich of the following is wrong- (1) p∨~p is a tautology (2) ~(~p)<→p is s a tautology (3) p∧~p is a contradiction (4) ((p∧p)→q)→p is a tautology
View Solution~[p∨(~q)] is equal to-
View SolutionIf the statement (p∗~q)→(p_q) is a tautology where ∗,_∈(∧,∨) then correct options is
View SolutionThe negation of the statement =[(~p∧q)∨(p∧~q)] is
View Solution

