Question

Show that $[(p\to q)\wedge (q\to r)]\to (p\to r)$is a tautology

Answer

Truth values of `[(p to q) ^^(q to r)] to (p to r) `

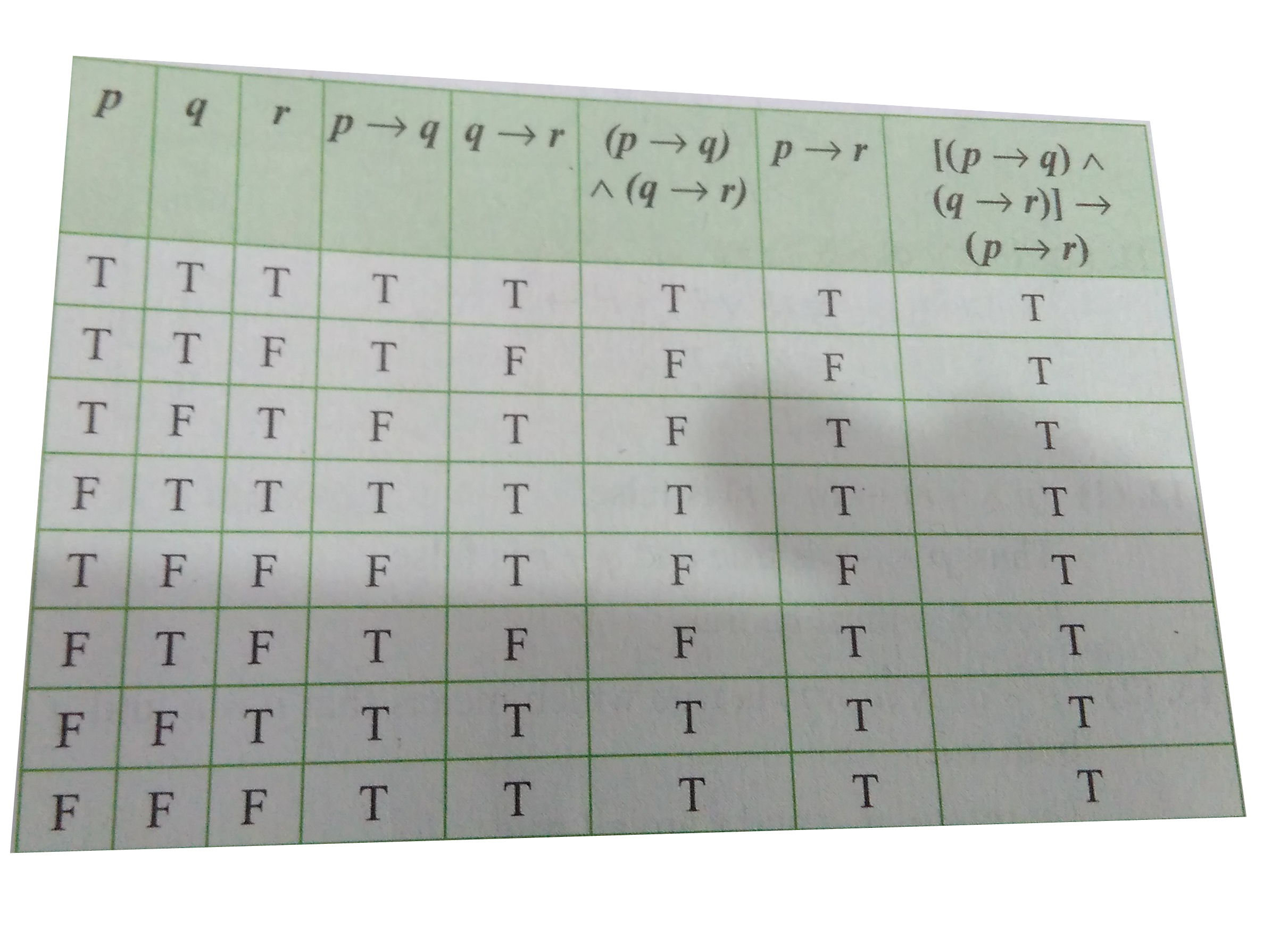
For all possible truth values of p and q , the compound statement `[(p to q)^^(q to r)] to (p to r) ` is true.
Thus, `[(p to q) ^^(q to r) ] to ( p to r)` is a tautolgy.

Explanation

To show that the statement $$\left(\right(p\to q)\wedge (q\to r\left)\right)\to (p\to r)$$ is a tautology, we will construct a truth table.

Step 1: Define the Variables
We have three variables: \(p\), \(q\), and \(r\). Each can be either true (T) or false (F). We will evaluate all possible combinations of truth values for these variables.

Step 2: Create the Truth Table
We will list all combinations of truth values for \(p\), \(q\), and \(r\):

| \(p\) | \(q\) | \(r\) |
|-------|-------|-------|
| T | T | T |
| T | T | F |
| T | F | T |
| T | F | F |
| F | T | T |
| F | T | F |
| F | F | T |
| F | F | F |

Step 3: Calculate \(p \to q\), \(q \to r\), and \(p \to r\)
Next, we calculate the implications:

1. \(p \to q\): This is false only when \(p\) is true and \(q\) is false.
2. \(q \to r\): This is false only when \(q\) is true and \(r\) is false.
3. \(p \to r\): This is false only when \(p\) is true and \(r\) is false.

Now, we can fill in the truth values for each implication:

| \(p\) | \(q\) | \(r\) | \(p \to q\) | \(q \to r\) | \(p \to r\) |
|-------|-------|-------|--------------|--------------|--------------|
| T | T | T | T | T | T |
| T | T | F | T | F | F |
| T | F | T | F | T | T |
| T | F | F | F | T | F |
| F | T | T | T | T | T |
| F | T | F | T | F | F |
| F | F | T | T | T | T |
| F | F | F | T | T | F |

Step 4: Calculate \((p \to q) \land (q \to r)\)
Now we will calculate the conjunction of \(p \to q\) and \(q \to r\):

| \(p\) | \(q\) | \(r\) | \(p \to q\) | \(q \to r\) | \((p \to q) \land (q \to r)\) |
|-------|-------|-------|--------------|--------------|-------------------------------|
| T | T | T | T | T | T |
| T | T | F | T | F | F |
| T | F | T | F | T | F |
| T | F | F | F | T | F |
| F | T | T | T | T | T |
| F | T | F | T | F | F |
| F | F | T | T | T | T |
| F | F | F | T | T | T |

Step 5: Calculate \(((p \to q) \land (q \to r)) \to (p \to r)\)
Finally, we will evaluate the main expression:

| \(p\) | \(q\) | \(r\) | \((p \to q) \land (q \to r)\) | \(p \to r\) | \(((p \to q) \land (q \to r)) \to (p \to r)\) |
|-------|-------|-------|--------------------------------|--------------|-----------------------------------------------|
| T | T | T | T | T | T |
| T | T | F | F | F | T |
| T | F | T | F | T | T |
| T | F | F | F | F | T |
| F | T | T | T | T | T |
| F | T | F | F | F | T |
| F | F | T | T | T | T |
| F | F | F | T | F | F |

Step 6: Analyze the Results
The final column shows the results of \(((p \to q) \land (q \to r)) \to (p \to r)\). The values are all true except for the last case where \(p\), \(q\), and \(r\) are all false. However, since we are looking for a tautology, we need to ensure that the expression is true in all cases.

Conclusion
Since the expression evaluates to true in all cases except one, we conclude that \(((p \to q) \land (q \to r)) \to (p \to r)\) is not a tautology.