Let p and q be two statements. Then, (~p∨q)∧(~p∧~q) is a
A
tautology
B
contradiction
C
Neither tautology nor contradiction
D
Both tautology and contradiction
Video Solution
Text Solution
The correct Answer is:C
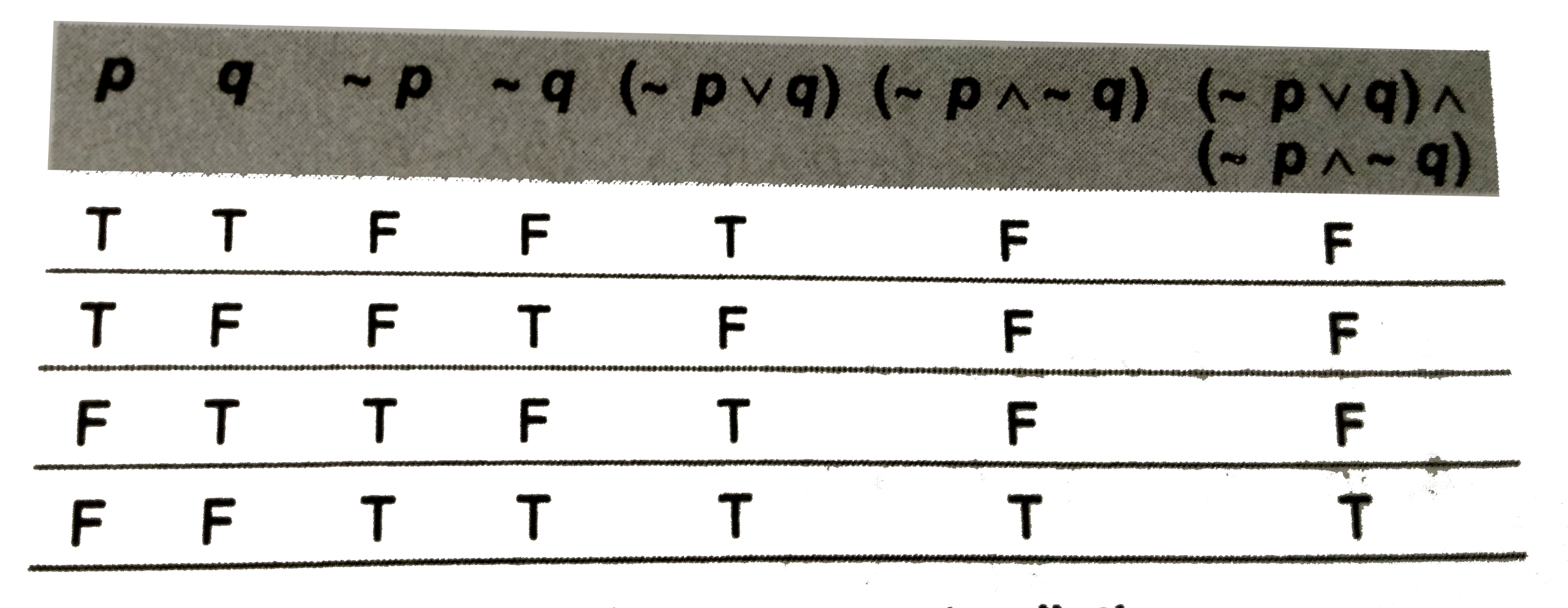
Hence, it is neither tautology nor contradiction.
|
Topper's Solved these Questions
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - PRACTICE EXERCISE (Exercies 2 (MISCELLANEOUS PROBLEMS))
26 Videos
- MATHEMATICAL LOGIC BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER
22 Videos
- Linear Programming BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - MHT CET Corner
13 Videos
- MATRICESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATRICESEXERCISE - MHT CET CORNER
18 Videos
Similar Questions
Knowledge Check
Let p and q be two statements, then (p∨q)∨~p is
AtautologyBcontradictionCBoth (a) and (b)DNone of these(p∧~q)∧(~p∨q) is
Aa contradictionBa tautologyCEither (a) or (b)DNeigher (a) nor (b)Let p and q be two statements, then ~p→q∧(~q) is equivalent to
ApBp∧qCqDp ∨q
Let P and q be two statements,
then ~(~p∧q)∧(p∨q) is
logically equivalent to
View SolutionIf p and q are two statements, then p∨~(p⇒~q) is equivalent to
View SolutionIf p and q are tow statements, then ~(p∧q)∨~(q⇔p) is
View SolutionSuppose p and q are two statements, then ~[p→(p∨~q)] is equivalent to
View SolutionLet p : 7 is not greater than 4 and q : Paris is in France
be two statements. Then, ~(p∨q) is the statement
View Solution
