If a graph is plotted between velocity (v) and displacement (y) of a particle executing SHM from mean position, then the nature of the graph is
Straight line
Parabola
Ellipse
Hyperbola
The correct Answer is:3
To determine the nature of the graph plotted between velocity (v) and displacement (y) of a particle executing Simple Harmonic Motion (SHM) from the mean position, we can follow these steps:
1. Understand the equations of SHM:
The displacement x of a particle in SHM can be expressed as:
x(t)=Asin(ωt+ϕ)
where A is the amplitude, ω is the angular frequency, and ϕ is the phase constant.
2. Find the velocity:
The velocity v of the particle is the time derivative of displacement:
v(t)=dxdt=Aωcos(ωt+ϕ)
3. Relate velocity to displacement:
We can express v in terms of x. From the SHM equations, we know:
v2=(Aω)2cos2(ωt+ϕ)
Using the identity cos2(θ)=1−sin2(θ), we can relate cos2(ωt+ϕ) to x:
cos2(ωt+ϕ)=1−sin2(ωt+ϕ)=1−(xA)2
Therefore:
v2=(Aω)2(1−(xA)2)
Simplifying gives:
v2=A2ω2−ω2x2
4. Rearranging the equation:
Rearranging the equation gives:
v2A2ω2+x2A2=1
This is the standard form of the equation of an ellipse.
5. Conclusion about the graph:
Since the equation we derived is in the form of an ellipse, the graph of velocity (v) versus displacement (x) will be an ellipse.
Final Answer:
The nature of the graph plotted between velocity (v) and displacement (y) of a particle executing SHM is an ellipse.
---
The displacement x of a particle in SHM can be expressed as:
x(t)=Asin(ωt+ϕ)
where A is the amplitude, ω is the angular frequency, and ϕ is the phase constant.
The velocity v of the particle is the time derivative of displacement:
v(t)=dxdt=Aωcos(ωt+ϕ)
We can express v in terms of x. From the SHM equations, we know:
v2=(Aω)2cos2(ωt+ϕ)
Using the identity cos2(θ)=1−sin2(θ), we can relate cos2(ωt+ϕ) to x:
cos2(ωt+ϕ)=1−sin2(ωt+ϕ)=1−(xA)2
Therefore:
v2=(Aω)2(1−(xA)2)
Simplifying gives:
v2=A2ω2−ω2x2
Rearranging the equation gives:
v2A2ω2+x2A2=1
This is the standard form of the equation of an ellipse.
Since the equation we derived is in the form of an ellipse, the graph of velocity (v) versus displacement (x) will be an ellipse.
The nature of the graph plotted between velocity (v) and displacement (y) of a particle executing SHM is an ellipse.
Topper's Solved these Questions
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION-C )
11 Videos
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT (SECTION -D( Comprehension) )
1 Video
- OSCILLATIONSBOOK - AAKASH INSTITUTECHAPTER - OSCILLATIONSEXERCISE - ASSIGNMENT ( SECTION -A)
58 Videos
- NUCLEIBOOK - AAKASH INSTITUTECHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
- PHYSICAL WORLDBOOK - AAKASH INSTITUTECHAPTER - PHYSICAL WORLDEXERCISE - ASSIGNMENT (Section-B)
5 Videos
Similar Questions
A graph between velocity and displacement of a particle performing SHM is shown. Find the acceleration when the particle is at half of maximum displacement from mean position.
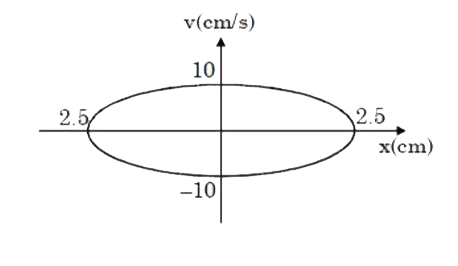
View SolutionIf a graph is plotted between angular velocity ω and distance x of a particle performing uniform circular motion, the graph is a straight line
View Solution
Knowledge Check
Graph between velocity and displacement of a particle, executing S.H.M. is
AA straight lineBA parabolaCA hyperbolaDAn ellipseThe graph plotted between acceleration and displacement of a particle in SHM is
Aa straight lineBa circleCan ellipseDa hyperbolaThe shape of graph plotted between velocity and position of a particle executing simple harmonic motion is
AA straight lineBAn ellipseCA parabolaDA hyperbola
The graph between total energy and displacement of a particle performing S.H.M. is
View SolutionThe graph between velocity and displacement of a particle executing S.H.M. of angular frequency 1 rad/s can be (where A is the amplitude of displacement)
View SolutionThe graph between potential energy and displacement of a particle performing S.H.M. is
View SolutionThe graph between kinetic energy and displacement of a particle performing S.H.M. is
View SolutionThe figure shows a graph between velocity and displacement (from mean position) of a particle performing SHM:
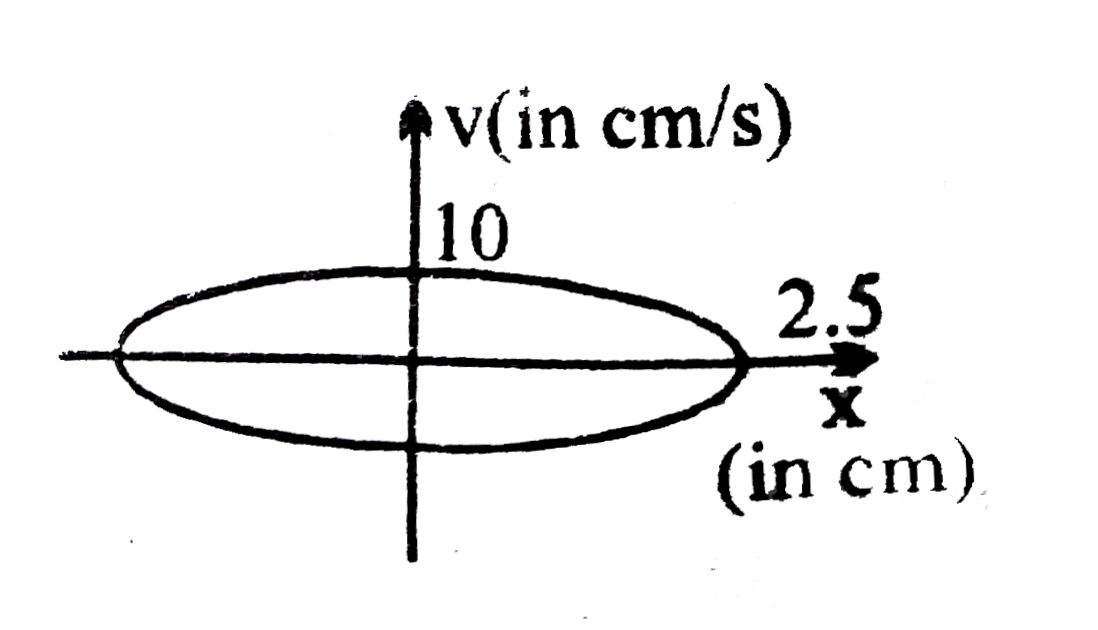
View Solution
