B and C are two identicalsphereskeptincontact with eachother on a horizontalfrictionaless floor.Another identicalspherea A moving with velocity u along the common tangent to B and C strikes B and C simultaneously.

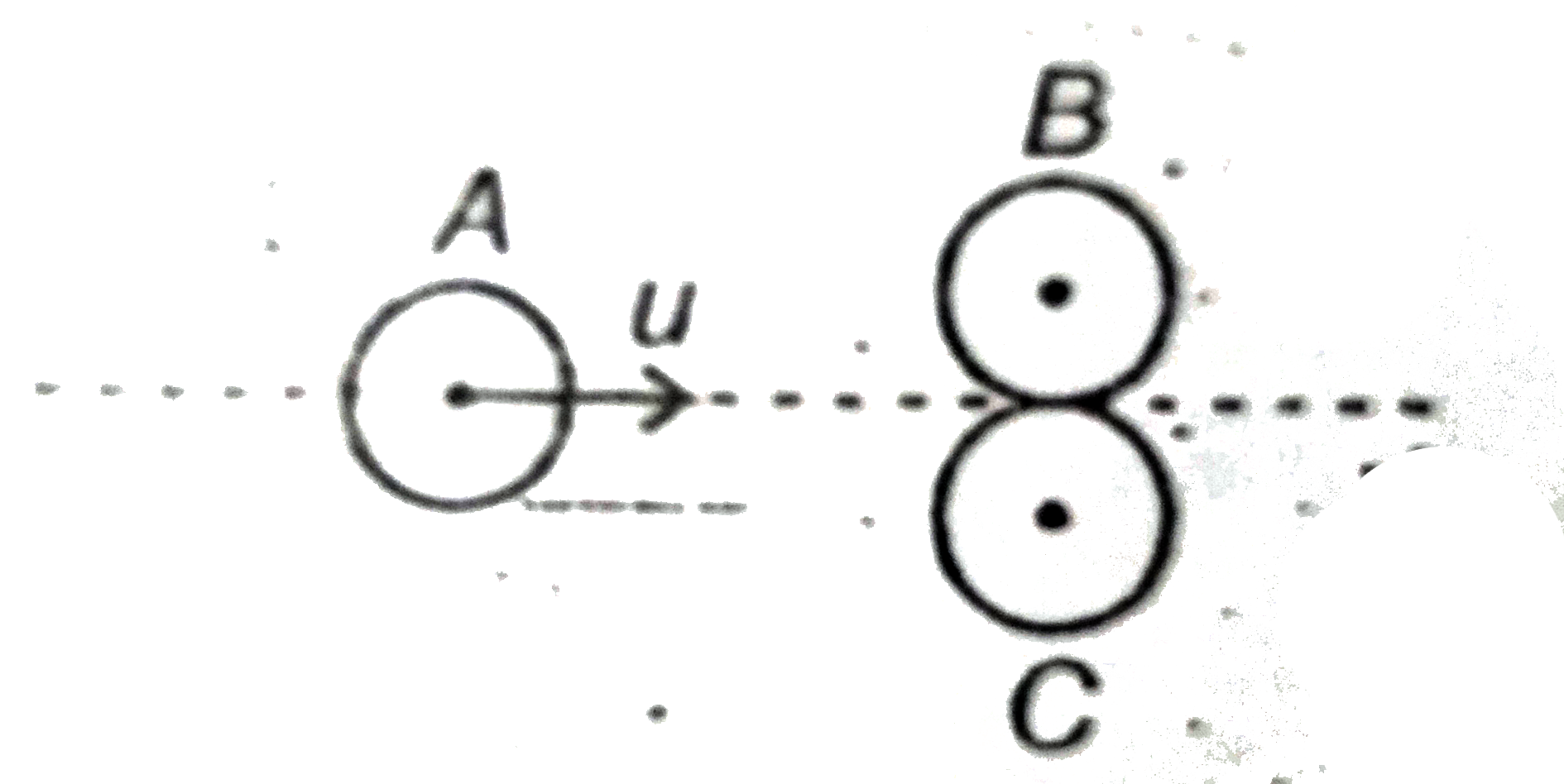
Find their velocties after collision if
(a) Collision is elastic
(b) Collision is inelastic with coefficient of restitution e.

Video Solution

Text Solution

Verified by Experts

By conservation oflinear momentumalongy-axis,
$m v_{2} {sin 30}^{\circ} - m v_{3} {sin 30}^{\circ} = 0$
$\Rightarrow v_{2} = v_{3} = v_{o} (s a y) \dots (1)$
By conservation of linear momentum along x-axis
$m u = m v_{1} + m v_{2} {cos 30}^{\circ} + m v_{3} {cos 30}^{\circ}$
$v = v_{1} + 2 v_{0} {cos 30}^{\circ}$
$v = v_{1} + \sqrt{3} v_{0} ... (2)$
Coefficient of restitution,
$e = \frac{v_{separation}}{v_{approach}}$
$1 = \frac{v_{0} - v_{1} {cos 30}^{\circ}}{u {cos 30}^{\circ}} .$ (for elastic collision)
$\Rightarrow \frac{\sqrt{3} u}{2} = v_{0} - \frac{v_{1} \sqrt{3}}{2}$
$u = \frac{2 v_{0}}{\sqrt{3}} - v_{1} ... (3)$
Adding equation (1) and (2),
$2 u = \sqrt{3} v_{0} + \frac{2 v_{0}}{\sqrt{3}} = \frac{3 v_{0} + 2 v_{0}}{\sqrt{3}}$
$u = \frac{5 v_{0}}{2 \sqrt{3}} \Rightarrow v_{0} = \frac{2 \sqrt{3} u}{5} ... (4)$
Putting value of $v_{0}$ in equation (3),
$v_{1} = \frac{2 v_{0}}{\sqrt{3}} - u = \frac{2}{\sqrt{3}} \frac{¯ 2 \sqrt{3 u}}{5} - u$
$= \frac{4 u}{5} - u$
$= - \frac{u}{5} ... (5)$
(b) For inelastic collision
Total momentum of the system is conserved. We obrtain the same equations as in part (a) $\Rightarrow Equation (1) v_{1} = v_{3} = v_{0}$
Equation $(2) u = v_{1} + \sqrt{3} v_{0}$
Coefficient of restitution.
$e = \frac{v_{0} - v_{1} {cos 30}^{\circ}}{u {cos 30}^{\circ}}$
$\Rightarrow e u \frac{\sqrt{3}}{2} = v_{0} v_{1} \frac{\sqrt{3}}{2}$
$\Rightarrow u = \frac{2 v_{0}}{e \sqrt{3}} - \frac{v_{1}}{2} ... (6)$
Dividing equation (2) by e,
$\frac{u}{e} = \frac{v_{1}}{e} + \frac{\sqrt{3} v_{0}}{e}$
Equation (6): $u = \frac{2 v_{0}}{e \sqrt{3}} - \frac{v_{1}}{e}$
Adding, $u (\frac{1}{e} + 1) = \frac{1}{e} [\frac{5 v_{0}}{\sqrt{3}}]$
$\Rightarrow v_{0} = \frac{\sqrt{3} u}{5} (1 + e) ... (7)$
Putting value of $v_{0}$ in equation (6),
$v_{1} = (\frac{2 v_{0}}{\sqrt{3}} - e u)$
$= \frac{u}{5} (2 - 3 e) ... (8)$

Updated on:21/07/2023