An object of mass m moving with speed u collides one dimentionally with another identical object at rest. Find their velocities after collision, if coefficient of restitution of collision is e.

Video Solution

Text Solution

Verified by Experts

Let $v_{1}$ and $v_{2}$ be the final velocities of 1st and 2nd object respectively.
$v_{1} = (\frac{1 - e}{2}) u$ and $v_{2} = (\frac{1 + e}{2}) u$

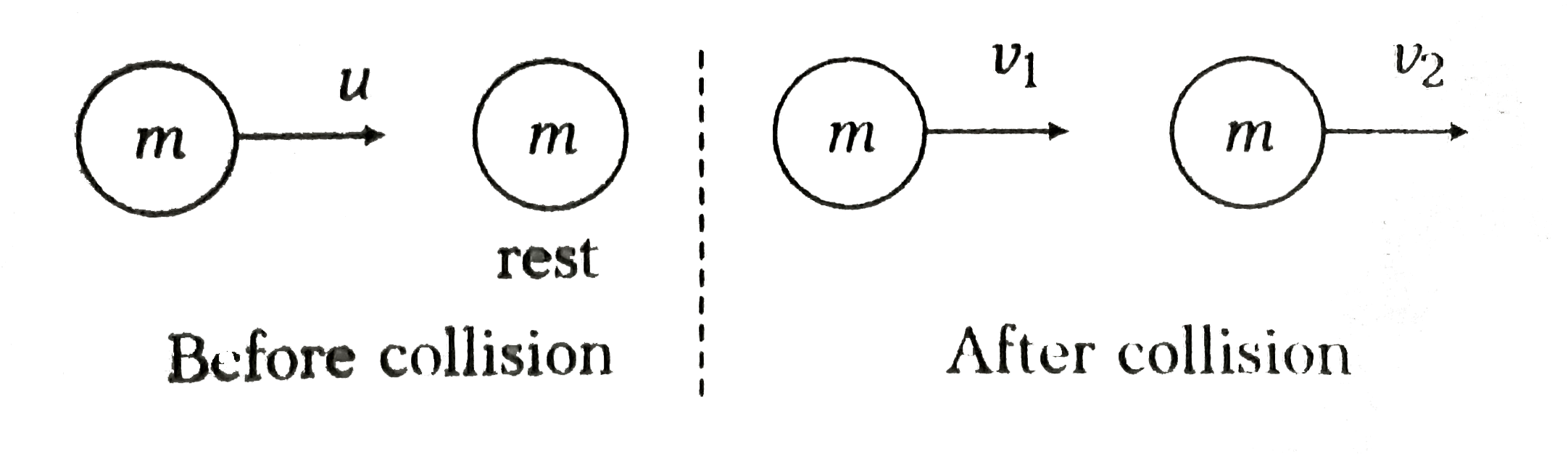
By law of conservation of momentum $μ + m \times 0 = m v_{1} + m v_{2}$
$\Rightarrow v_{1} + v_{2} = u$ ..................(ii)
Now, $e = \frac{v_{2} - v_{1}}{u_{1} - u_{2}} \Rightarrow \frac{v_{2} - v_{1}}{u} = e$
$\Rightarrow v_{2} - v_{1} = e u$ ............(ii)
Adding Eqs. (i) and (ii)
$2 v_{2} = u + e u \Rightarrow v_{2} = [\frac{1 + e}{2}] u$
Subtracting Eq. (ii) from Eq. (i)
$2 v_{1} = (1 - e) u \Rightarrow v_{1} = [\frac{1 - e}{2}] u$

|

Updated on:21/07/2023

Class 11 PHYSICS CENTRE OF MASS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
A $\frac{3}{4} μ^{2}$
B $\frac{3}{8} μ^{2}$
C $\frac{1}{4} μ^{2}$
D $\frac{1}{8} μ^{2}$
Question 2 - Select One
A particle of mass m, collides with another stationary particle of mass M. If the particle m stops just after collision, then the coefficient of restitution for collision is equal to
A1
B $\frac{m}{M}$
C $\frac{M - m}{M + m}$
D $\frac{m}{M + m}$
Question 3 - Select One
An object of mass $M_{1}$ moving horizontally with speed u collides elastically with another object of mass $M_{2}$ at rest. Select correct statement.

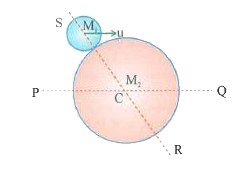AThe momentum of system is conserved only in direction PQ
BMomentum of $M_{1}$ is conserved in direction perpendicular to SR
CMomentum of $M_{2}$ will change in direction normal to CR
DAll of these

DC PANDEY-CENTRE OF MASS-Medical entrances gallery

Home
Ask Doubt
Profile