Two indentical balls A and B moving with velocities uA and uB I the same direction collide. Coefficient of restitution is e.
(a) Deduce expression for velocities of the balls after the collision.
(b) If collision is perfectly elastic, what do you observe?
Equation expressing momentum conservation is
vA+vB=uA+uB …(A)
Equation of coefficient of restitution is
vB−vA=euA−eUBm …(B)
(a) From the above two equations, velocities vA and vB are
vA=(1−e2)uA+(1+e2)uB ...(i)
vB=(1+e2)uA+(1−e2)uB ...(ii)
(b) For perfectly elastic impact e=1, velocities vA and vB are
vA=uB ...(iii)
vB=uA ...(iv)
Identical bodies exchange their velocities after perfectly elastic impact.
Topper's Solved these Questions
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-I
Explore 40 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-II
Explore 43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:EXERCISE-IV ASSERTION & REASON
Explore 11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 5 B (Integer Type Questions)
Explore 3 Videos
Similar Questions
A ball collides with a frictionless wall with velocity u as shown in the figure. Coefficient of restitution for the impact is e.
(a) Find expression for the velocity of the ball immediately after the impact.
(b) If impact is perfectly elastic what do you observe?
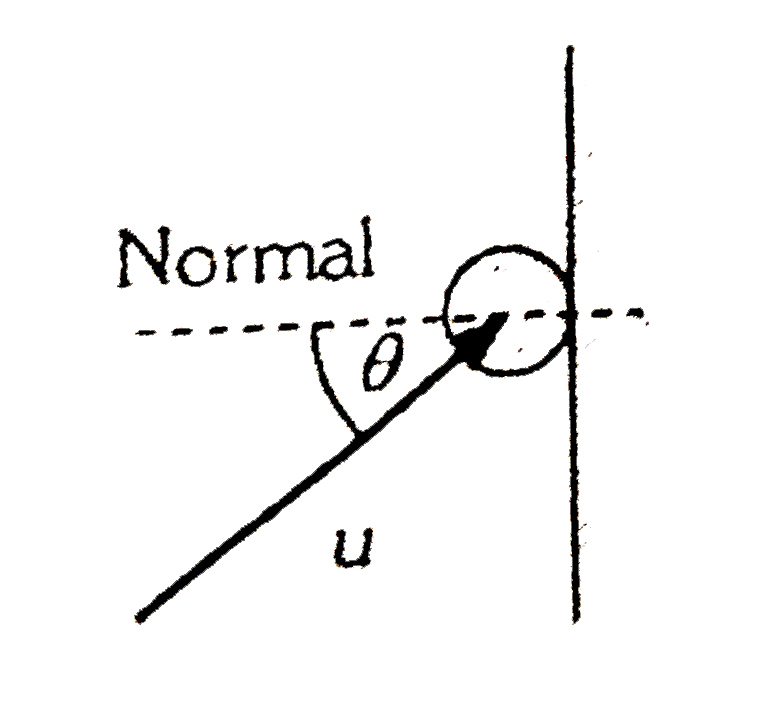
View SolutionA collision occurs between two identical balls each of mass m, moving with velocities →u1 and →u2, colliding head-on. The coefficient of restitution is 0.5. The energy lost in the collision is:
View Solution
Knowledge Check
A sphere A impinges directly on an identical sphere B at rest. If coefficient of restitution is e , the ratio of velocities of A and B after collision is
A1−e1+eB1+e1−eCe1+eD2e1+eA ball of mass m moving with a constant velocity strikes against a ball of same mass at rest. If e= coefficient of restitution, then what will the the ratio of the velocities of the two balls after collision?
A1−e1+eBe−1e+1C1+e1−eD2+ee−1A ball moving with velocity 2 m/s collides head on with another stationary ball of double the mass. If the coefficient of restitution is 0.5, then their velocities (in m/s) after collision will be
A0,1B1,1C1, 0.5D0,2
A ball P is moving with a certain velocity , collides head-on with another ball Q of same mass is rest. The coefficient of restitution is 1/4, then ratio of velocity of P and Q just after the collision is
View SolutionTwo identical bodies A and B moving with velocities 13 m/s and - 15 m/s respectively collide head-on elastically. What will be their velocities after collision?
View SolutionA ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
View SolutionA sphere of mass m moving with a velocity u hits another stationary sphere of same mass. If e is the coefficient of restitution, what is the ratio of the velocities of two spheres after the collision?
View SolutionThe first ball of mass m moving with the velocity υ collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, then the ratio of the velocities of the first and the second ball after the collision is
View Solution