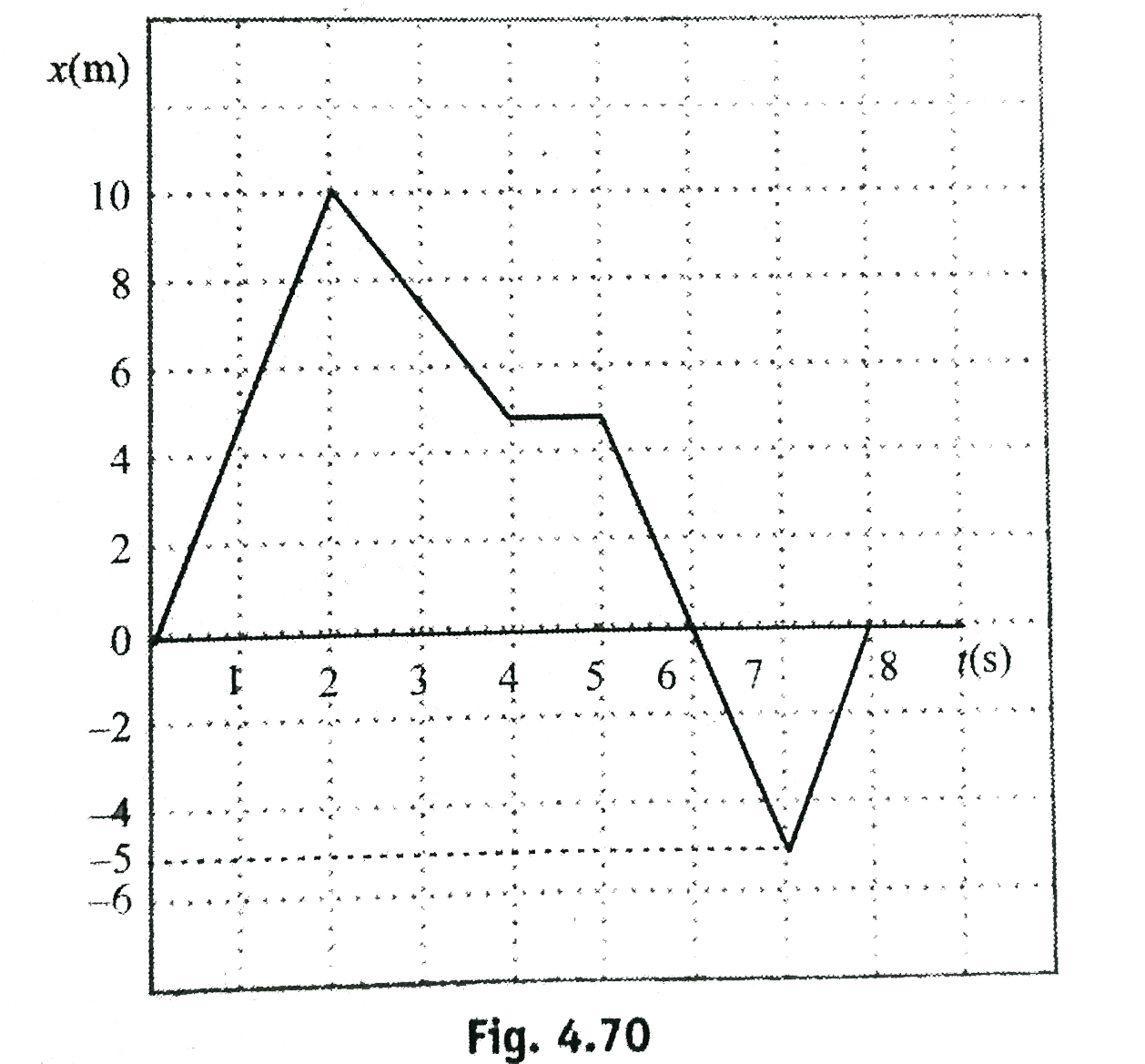
The v-t graph for a particle moving along x-axis is shown in the figure, find
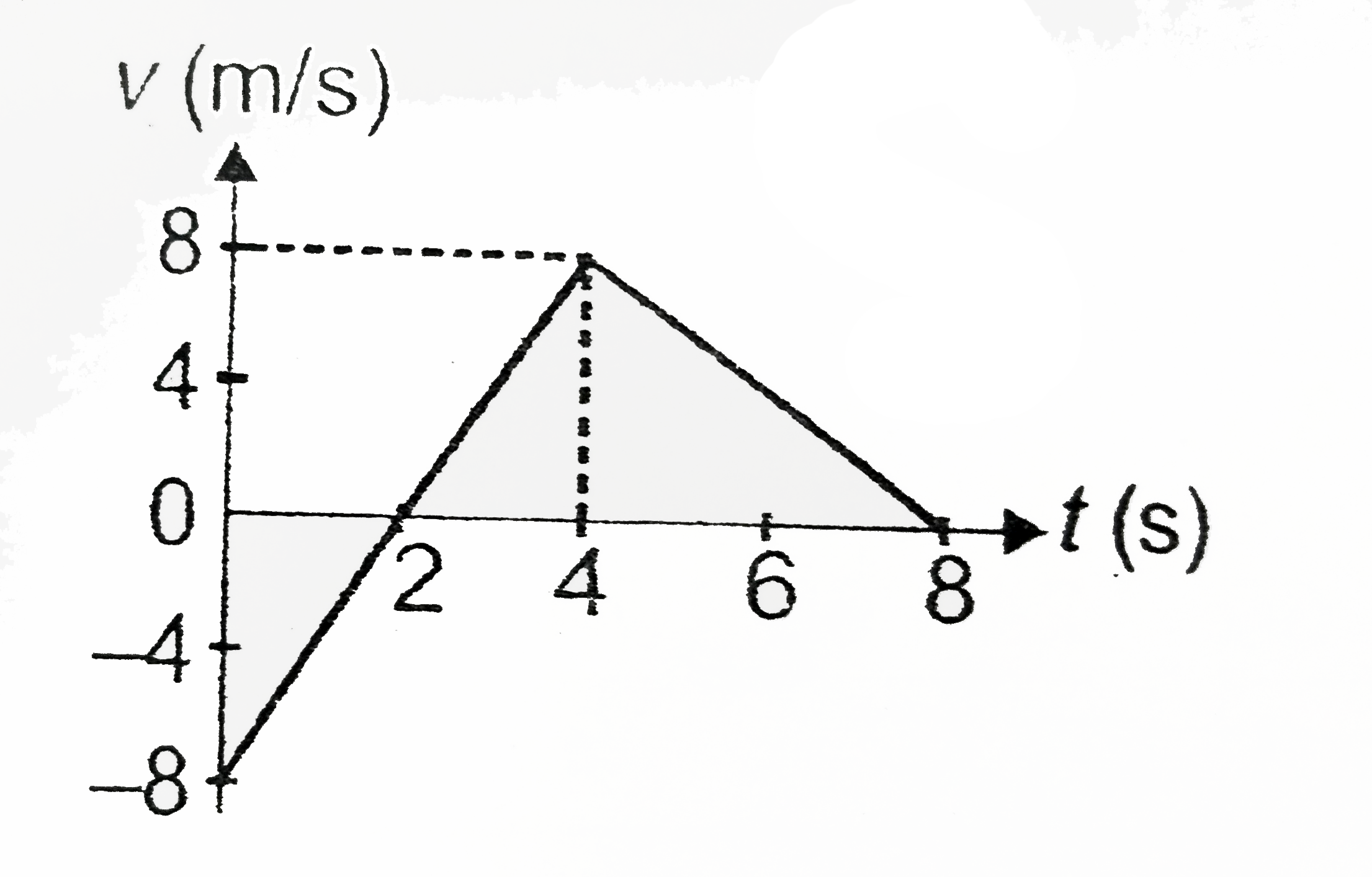
(a) Average velocity in the interval 0 to 8 s.
(b) Average speed in the interval 0 to 8 s.
(c) Average acceleration in the interval 0 to 4 s.
(d) Instantaneous acceleration at t = 2.5 s.
(a) Displacement in the interval 0 to 8 s is equal to the area under the graph, taking the area below time axis as negative.
⇒ Displacement=(−12×2×8)+(12×6×8)
= 16 m
Average velocity=displacementtime interval=168=2m/s

(b) Distance in the interval of 0 8 s is equal to the area under the graph taking the both areas (above and below time axis) positive.
Distance=(12×2×8)+(12×6×8)
= 32 m
Average speed =distancetime interval
=328=4m/s
(c) Average acceleration=change in velocitytime interval
change in velocity in the interval 0 to 4 s
= (Velocity at t = 4 s)−(Velocity at t = 0 )=8−(−8)=16m/s ltbr> ⇒ Average acceleration=164=4m/s2
(d)
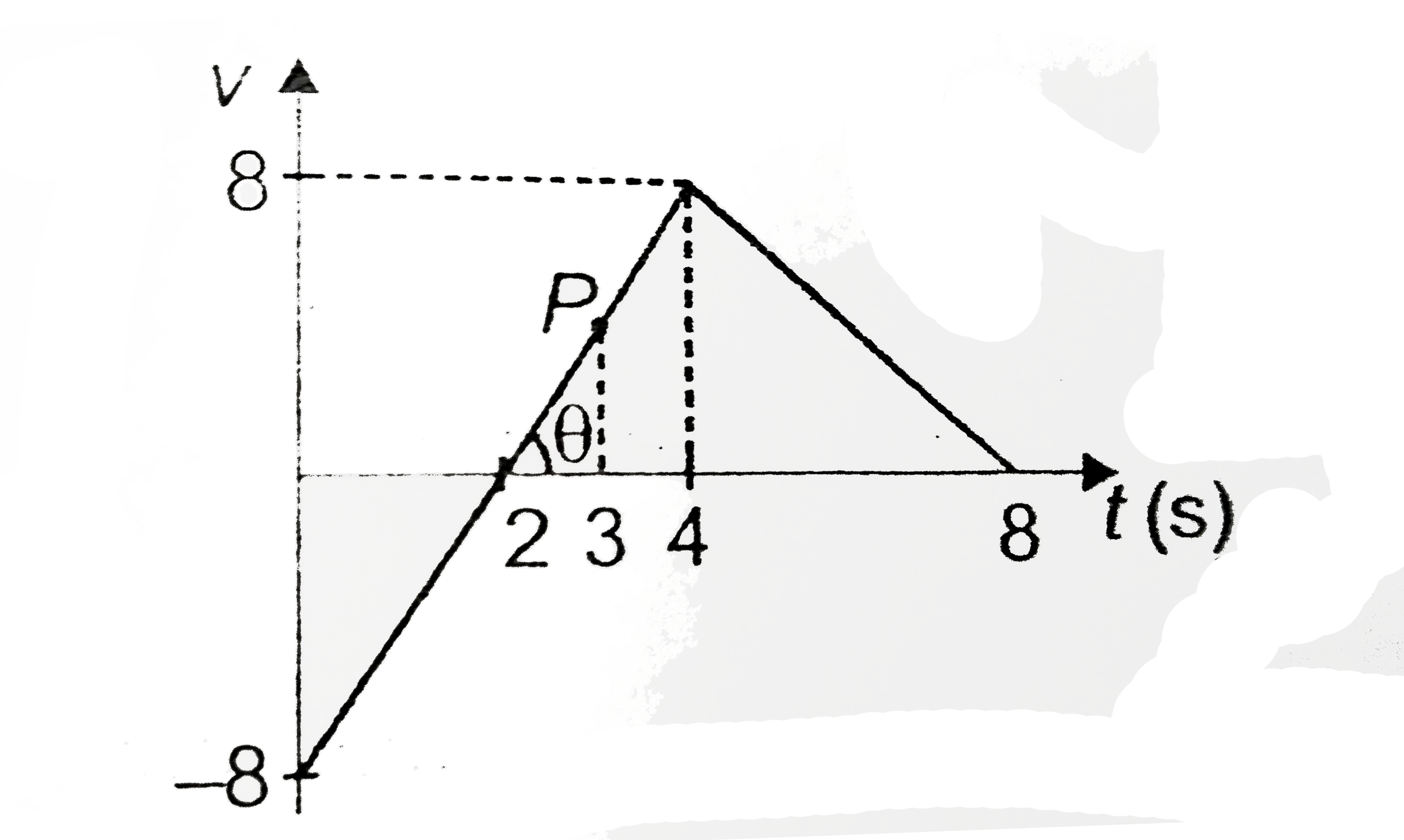
Instantaneous acceleration at t = 3 s is the slope of graph at point
P=tanθ=82=4m/s2
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Try Yourself
Explore 40 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - A)
Explore 50 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOVING CHARGE AND MAGNESIUMBook:AAKASH INSTITUTEChapter:MOVING CHARGE AND MAGNESIUMExercise:SECTION D
Explore 16 Videos
Similar Questions
Knowledge Check
Position-time graph for a particle moving along x− direction is as shown in the figure. Average speed of the particle from t=0 to t=4 is :
 A154m/sB103m/sC52m/sD54m/s
A154m/sB103m/sC52m/sD54m/sThe position (x) - time (t) graph for a particle moving along a straight line is shown in figure. The average speed of particle in time interval t = 0 to t = 8 s is
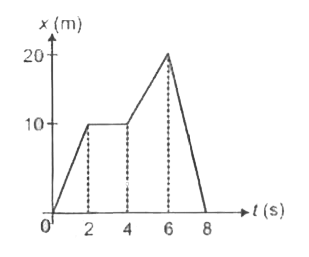 AZeroB5 m/sC7.5 m/sD9.7 m/s
AZeroB5 m/sC7.5 m/sD9.7 m/sVelocity-time graph of a particle moving in a straight line is shown in figure. In the time interval from t = 0 to t = 14 s, find:
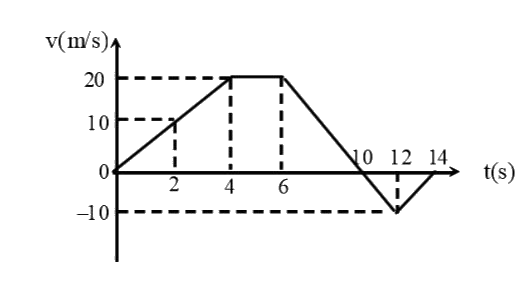
Q. average speed of the particleA20m/sB40m/sC10m/sD30m/s
A particle is moving in a straight line. Its displacement at any instant t is given by x=10t+15t3, where x is in meters and t is in seconds. Find
(i) the average acceleration in the intervasl t = 0 to t = 2s and
(ii) instantaneous acceleration at t = 2 s.
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.

View SolutionThe position of an object moving on a straight line is defined by the relation x=t3−2t2−4t, where x is expressed in meter and t in second. Determine
(a) the average velocity during the interval of 1 second to 4 second.
(b) the velocity at t = 1 s and t = 4 s,
(c) the average acceleration during the interval of 1 second to 4 second.
(d) the acceleration at t = 4 s and
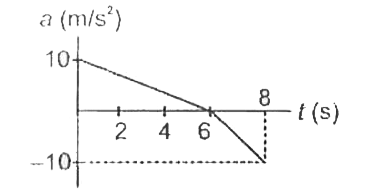
View SolutionThe acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
View SolutionThe velocity-time plot is shown in figure. Find the average speed in time interval t=0 to t=40s during the period.
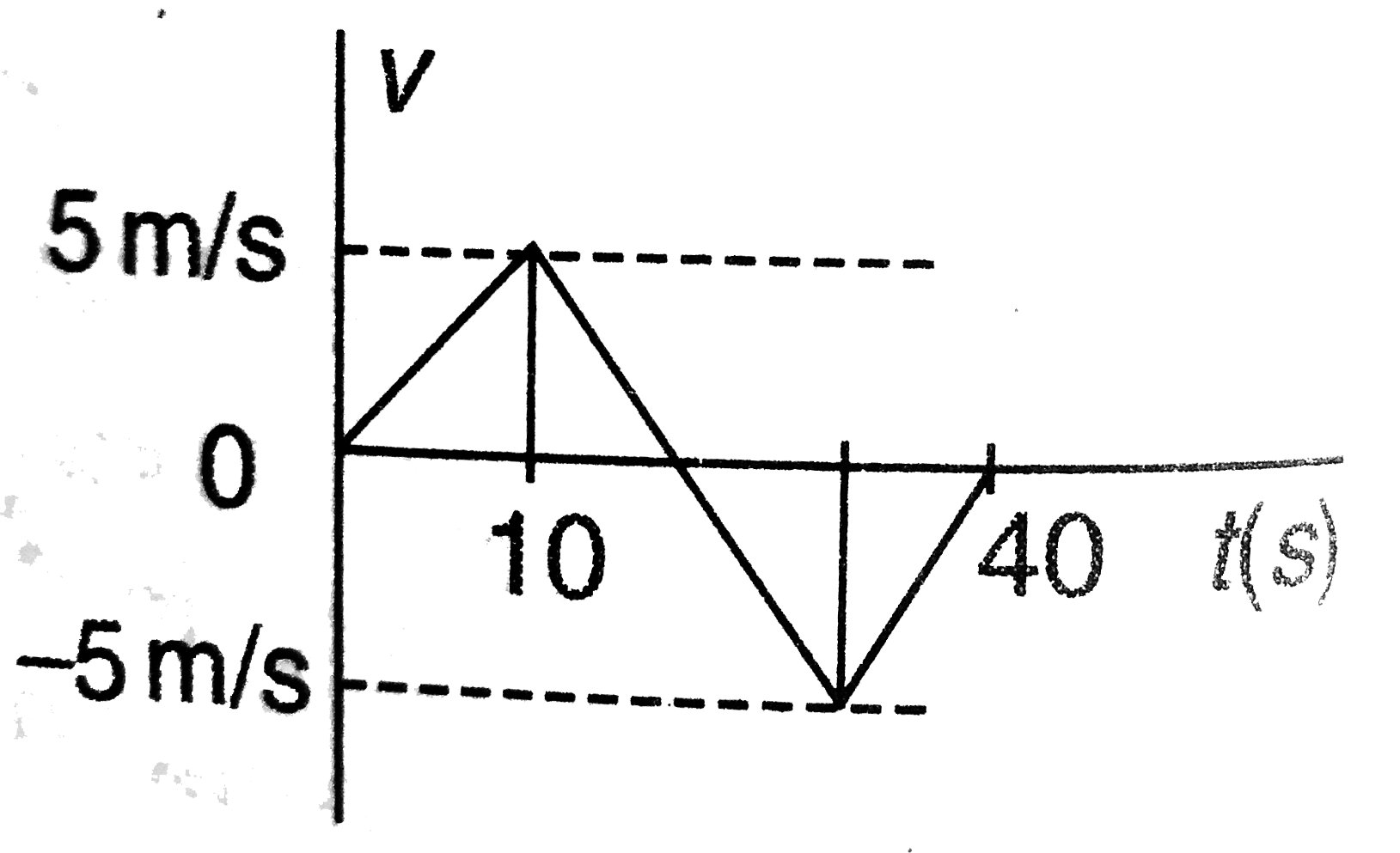
View Solution


 .
.