The position of an object moving on a straight line is defined by the relation , where x is expressed in meter and t in second. Determine
(a) the average velocity during the interval of 1 second to 4 second.
(b) the velocity at t = 1 s and t = 4 s,
(c) the average acceleration during the interval of 1 second to 4 second.
(d) the acceleration at t = 4 s and
(a) The position at
The position at
Average velocity in the interval
(b) By the term velocity we mean instantaneous velocity which is given by
At
At
(c) The average acceleration in an interval is given by
(d) The instantaneous acceleration is given by
At
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Try Yourself
Explore 40 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - A)
Explore 50 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTEChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOVING CHARGE AND MAGNESIUMBook:AAKASH INSTITUTEChapter:MOVING CHARGE AND MAGNESIUMExercise:SECTION D
Explore 16 Videos
Similar Questions
The position of a particle moving along a straight line is defined by the relation, x=t3−6t2−15t+40 where x is in meters and t in seconds.The distance travelled by the particle from t=0 to t=2 s is?
View SolutionThe position of a particle varies with time according to the relation x=3t2+5t3+7t, where x is in m and t is in s. Find
(i) Displacement during time interval t = 1 s to t = 3 s.
(ii) Average velocity during time interval 0 - 5 s.
(iii) Instantaneous velocity at t = 0 and t = 5 s.
(iv) Average acceleration during time interval 0 - 5 s.
(v) Acceleration at t = 0 and t = 5 s.
View Solution
Knowledge Check
The motion of a particle along a straight line is described by the function x=(2t−3)2, where x is in metres and t is in seconds. Find
(a) the position, velocity and acceleration at t=2s.
(b) the velocity of the particle at the origin .A1 , 0 , 4B1 , 4 , 0C10 , 14 , −34D10 , −1 , 0A particle is moving along straight line whose position x at time t is described by x=t3−t2 where x is in meters and tis in seconds . Then the average acceleration from t=2 sec. to t=4 sec, is :
A16m/s2B18m/s2C22m/s2D10m/s2The velocity v of a body moving along a straight line varies with time t as v=2t2e−t, where v is in m/s and t is in second. The acceleration of body is zero at t =
A0B2 sC3DBoth (1) & (2)
The displacement of a particla moving in straight line is given by s=t4+2t3+3t2+4, where s is in meters and t is in seconds. Find the
(a) velocity at t=1s, (b) acceleration at t=2s,
(c ) average velocity during time interval t=0 to t=2s and
(d) average acceleration during time interval t=0 to t=1s.
View Solution[" 4.If the particle is moving along a straight line "],[" given by the relation "x=2-3t+4t^(3)" where "s" is "],[" in cms.,and "t" in sec.Its average velocity "],[" during the third sec is "]
View SolutionThe v-t graph for a particle moving along x-axis is shown in the figure, find
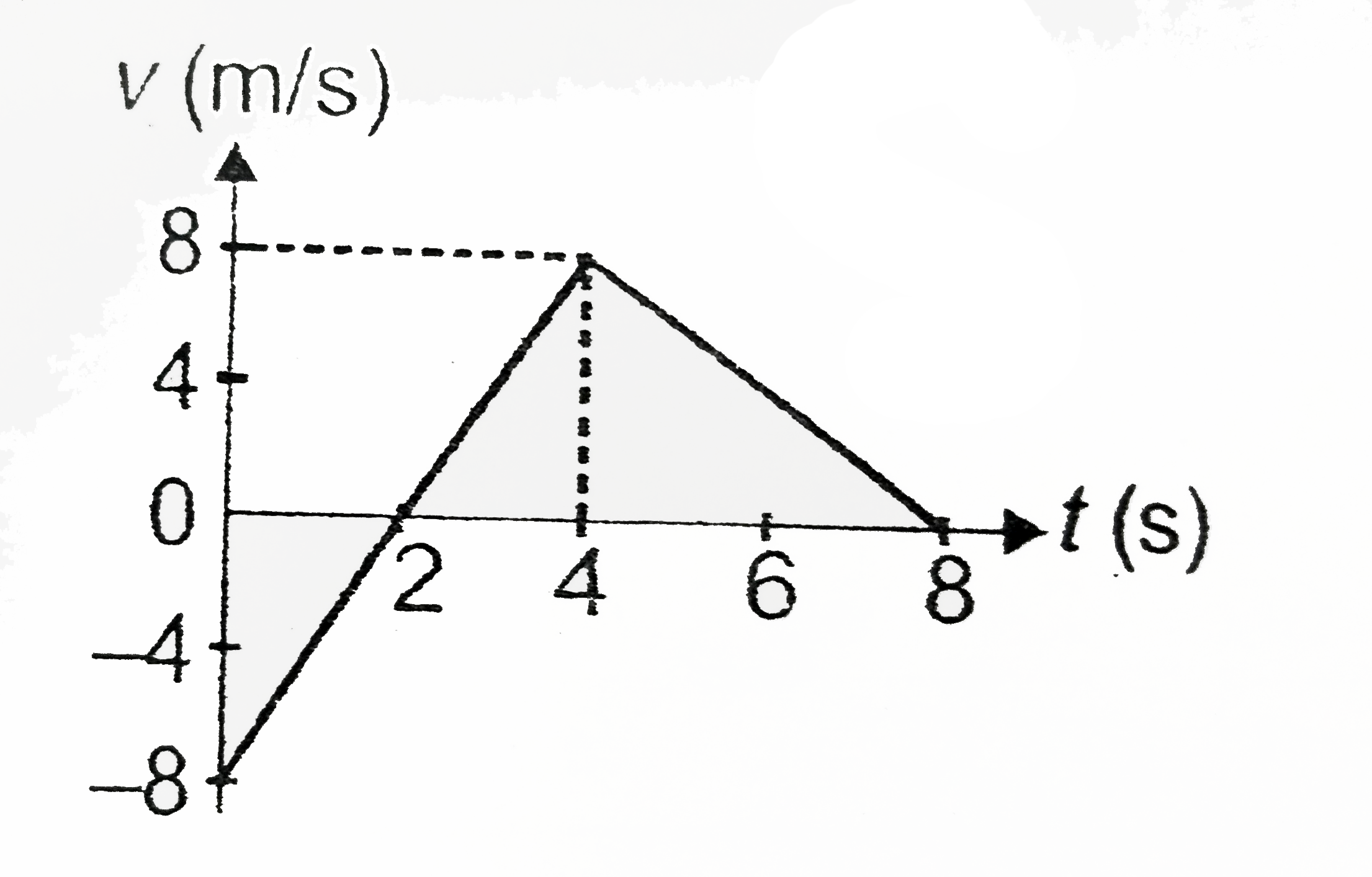
(a) Average velocity in the interval 0 to 8 s.
(b) Average speed in the interval 0 to 8 s.
(c) Average acceleration in the interval 0 to 4 s.
(d) Instantaneous acceleration at t = 2.5 s.
View SolutionThe velocity ofacar travelling on a straight road is given by the equation v=6+8t−t2 where vis in meters per second and t in seconds. The instantaneous acceleration when t=4.5s is :
View SolutionThe displacement of a particle moving in a straight line, is given by s=2t2+2t+4 where s is in metres and t in seconds. The acceleration of the particle is.
View Solution

