A body weight W,is projected vertically upwards from earth's surface to reach a height above the earth which is equal to nine times the radius of earth.The weight of the body at that height will be:
W100
W3
W91
W9
The correct Answer is:A
To solve the problem, we need to determine the weight of a body at a height above the Earth's surface that is equal to nine times the radius of the Earth. Let's break this down step by step.
Step 1: Understand the Weight Formula
The weight of a body at a distance r from the center of the Earth is given by the formula:
W′=G⋅M⋅mr2
where:
- W′ is the weight of the body at distance r,
- G is the universal gravitational constant,
- M is the mass of the Earth,
- m is the mass of the body,
- r is the distance from the center of the Earth.
Step 2: Determine the Distance from the Center of the Earth
The radius of the Earth is denoted as Re. The height above the Earth's surface is given as 9Re. Therefore, the total distance from the center of the Earth when the body is at this height is:
r=Re+9Re=10Re
Step 3: Substitute into the Weight Formula
Now, we can substitute r=10Re into the weight formula:
W′=G⋅M⋅m(10Re)2
This simplifies to:
W′=G⋅M⋅m100R2e
Step 4: Relate to Weight at Earth's Surface
The weight of the body at the Earth's surface is given by:
W=G⋅M⋅mR2e
Now, we can relate W′ to W:
W′=1100⋅G⋅M⋅mR2e=1100W
Step 5: Conclusion
Thus, the weight of the body at the height of 9Re above the Earth's surface is:
W′=W100
Final Answer
The weight of the body at that height will be W100.
---
The weight of a body at a distance r from the center of the Earth is given by the formula:
W′=G⋅M⋅mr2
where:
- W′ is the weight of the body at distance r,
- G is the universal gravitational constant,
- M is the mass of the Earth,
- m is the mass of the body,
- r is the distance from the center of the Earth.
The radius of the Earth is denoted as Re. The height above the Earth's surface is given as 9Re. Therefore, the total distance from the center of the Earth when the body is at this height is:
r=Re+9Re=10Re
Now, we can substitute r=10Re into the weight formula:
W′=G⋅M⋅m(10Re)2
This simplifies to:
W′=G⋅M⋅m100R2e
The weight of the body at the Earth's surface is given by:
W=G⋅M⋅mR2e
Now, we can relate W′ to W:
W′=1100⋅G⋅M⋅mR2e=1100W
Thus, the weight of the body at the height of 9Re above the Earth's surface is:
W′=W100
The weight of the body at that height will be W100.
Topper's Solved these Questions
Similar Questions
A body is projected vertically upwards from the earth's surface. The body reaches a height equal to one half of radius of earth. Calculate the initial speed with which the body was projected initially.
Radius of earth = 6,400 km
Mass of earth =6×1024kg
View SolutionA body is projected vertically upwards from the surface of earth with a velocity equal to half the escape velocity. If R be the radius of earth, maximum height attained by the body from the surface of earth is Rn. Find the value of n.
View Solution
Knowledge Check
If a body is to be projected vertically upwards from earth's surface to reach a height of 10R where R is the radius of earth. The velocity required to be si is
A√2411grB√2211grC√2011grD√1811grA body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A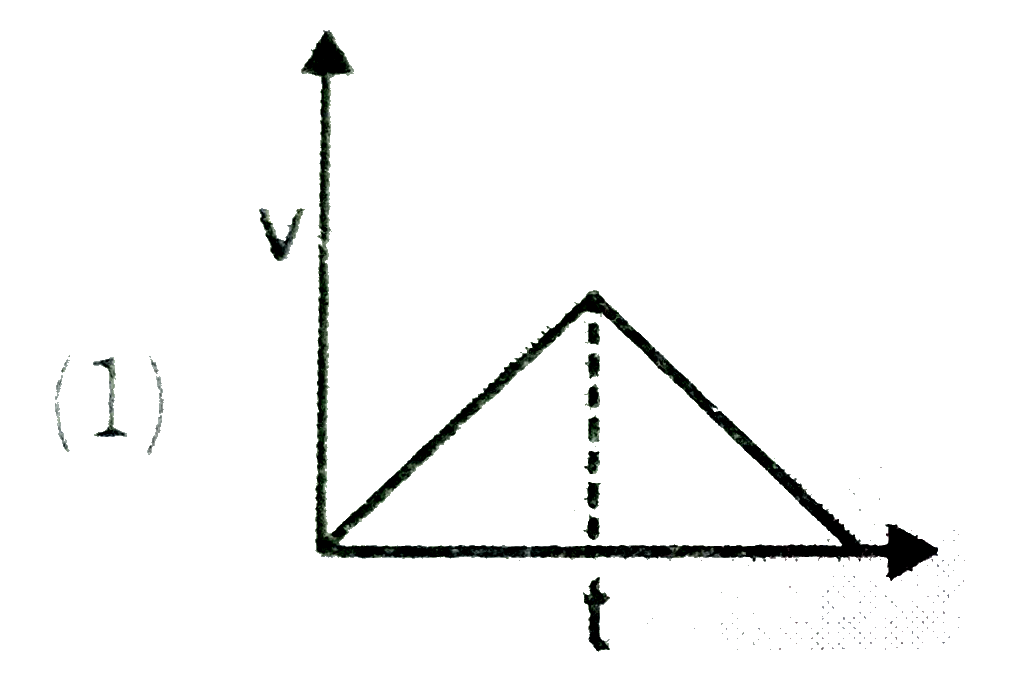 B
B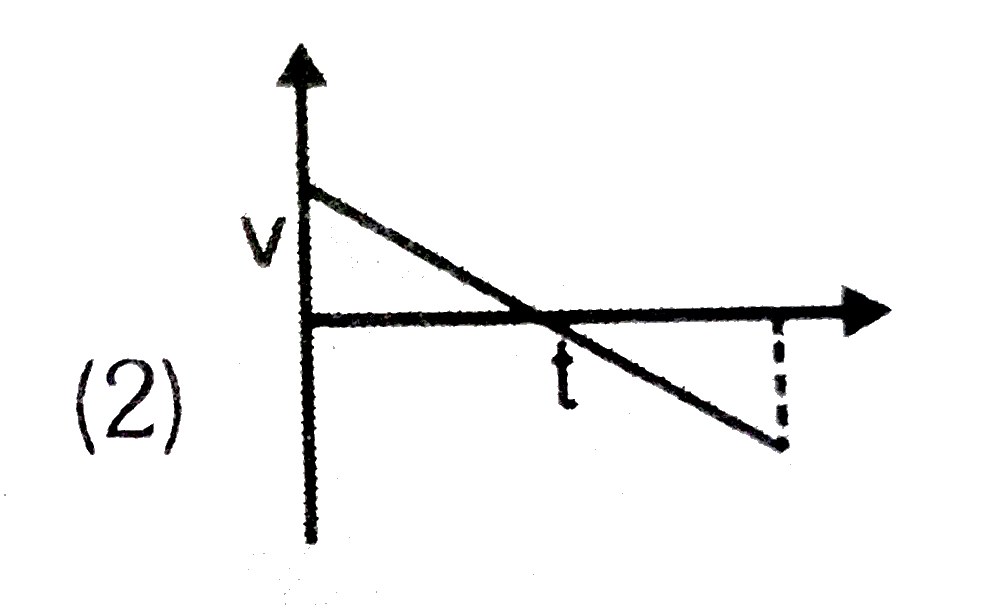 C
C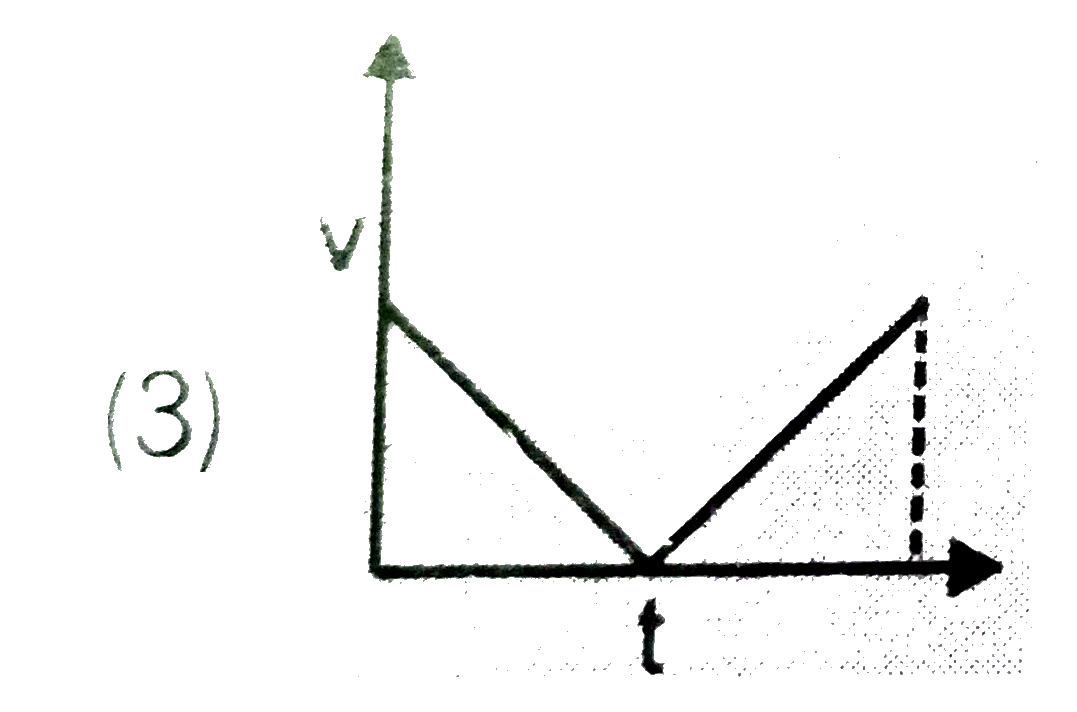 D
D
A body is to be projected vertically upwards from earth's surface to reach a height of 9R, where R is the radius of earth. What is the velocity required to do so? Given g=10ms−2 and radius of earth=6.4×106m.
A1.073×104ms−1B1.73×104ms−1C10.73×104ms−1D17.3×104ms−1
A body is projected vertically upward from the surface of earth with a velocity sufficient to carry it to initially. Calculate the time taken by it to reach height h.
View SolutionA body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If R is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionA body attains a height equal to the radius of the earth. The velocity of the body with which it was projected is
View SolutionA particle is throws vertically upwards from the surface of earth and it reaches to a maximum height equal to the radius of earth. The radio of the velocity of projection to the escape velocity on the surface of earth is
View SolutionA body attains a height equal to the radius of the earth. the velocity of the body with which is was projected is
View Solution
