Ratio of thermal energy released in two resistors R and 3R connected in parallel in an electric circuit is :
1:3
3:1
1:1
1:27
The correct Answer is:B
To find the ratio of thermal energy released in two resistors R and 3R connected in parallel, we can follow these steps:
Step 1: Understand the Concept
When resistors are connected in parallel, the potential difference (voltage) across each resistor is the same. The thermal energy E released in a resistor can be calculated using the formula:
E=V2R×t
where V is the voltage across the resistor, R is the resistance, and t is the time for which the current flows.
Step 2: Define the Resistors
Let:
- R1=R (the first resistor)
- R2=3R (the second resistor)
Step 3: Calculate Thermal Energy for Each Resistor
For the first resistor R1:
E1=V2R1×t=V2R×t
For the second resistor R2:
E2=V2R2×t=V23R×t
Step 4: Find the Ratio of Thermal Energies
Now, we can find the ratio of the thermal energies released in the two resistors:
E1E2=V2R×tV23R×t
Step 5: Simplify the Ratio
Notice that V2 and t cancel out:
E1E2=1/R1/(3R)=3RR=3
Final Answer
Thus, the ratio of thermal energy released in resistors R and 3R is:
E1E2=3:1
When resistors are connected in parallel, the potential difference (voltage) across each resistor is the same. The thermal energy E released in a resistor can be calculated using the formula:
E=V2R×t
where V is the voltage across the resistor, R is the resistance, and t is the time for which the current flows.
Let:
- R1=R (the first resistor)
- R2=3R (the second resistor)
For the first resistor R1:
E1=V2R1×t=V2R×t
E2=V2R2×t=V23R×t
Now, we can find the ratio of the thermal energies released in the two resistors:
E1E2=V2R×tV23R×t
Notice that V2 and t cancel out:
E1E2=1/R1/(3R)=3RR=3
Thus, the ratio of thermal energy released in resistors R and 3R is:
E1E2=3:1
Topper's Solved these Questions
Similar Questions
You take two resistors of resistance 2R and 3R and connect them in parallel in an electric circuit. Calculate the ratio of electric power consumed by 2R and 3R resistors.
View SolutionIf two resistors of R1 and R2 ohms are connected in parallel in an electric circuit to make an R ohm resistor, the value of R can be found from the equation,
1R=1R1+1R2
If R1 is decreasing at the rate of 1 ohm/sec and R2 i increasing at the rate of 0.5 ohm/sec, at what rate is R changing when R1=75 ohm and R2=50 ohm ?

View Solution
Knowledge Check
For three circuits, shown here
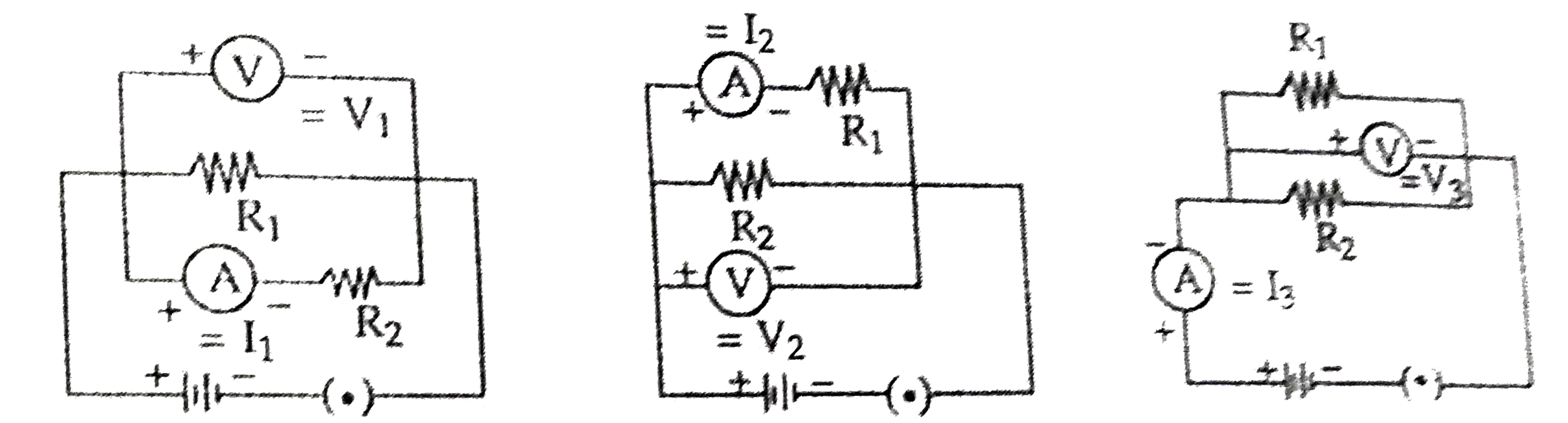
the same two resistors R1 and R2 have been connected in parallel in all the circuits but the voltmeter and the ammeter have been connected in three different positions. The relation between the three voltmeter and ammeter readings would be :AV1=V2=V3 and I1=I2=I3BV1≠V2≠V3 and I1=I2=I3CV1=V2=V3 and I1≠I2≠I3DV1≠V2≠V3 and I1≠I2≠I3Equivalent resistance R, of the parallel combination when two resistors Rand R, are connected in parallel is equal to
ARp=R1+R2R1R2BRp=R1R2R1−R2CRp=R1−R2R1+R2DRp=R1+R2R1+R2In a circuit containing two unequal resistors connected in parallel :
AThe current is the same in both the resistorsBA large current flows through the large resistorCThe voltage drop across both the resistances is the sameDThe small resistance has smaller conductance
Two resistances R and 2R are connected in parallel in an electric circuit. The thermal energy developed in R and 2R are in the ratio
View SolutionTwo resistors of 30Ωand60Ω are connected in parallel in an electric circuit. How does the current passing through the two resistors compare?
View SolutionTwo lamps have resistance r and R, R being greater than r. If they are connected in paralled in an electric circuit, then
View SolutionIn order to determine the equivalent resistance of two resistors R1 and R2 connected in series, a student made this circuit for his experiment.
The only statement which is true for this circuit is that it gives :

View SolutionTwo wires with resistances R and 2 R are connected in parallel, the ratio of heat generated in 2 R and R is
View Solution
