A body is projected vertically upward from the surface of earth with a velocity sufficient to carry it to initially. Calculate the time taken by it to reach height h.
To solve the problem of calculating the time taken by a body projected vertically upward from the surface of the Earth to reach a height h, we will use the principles of energy conservation and calculus. Here’s a step-by-step solution:
Step 1: Understand the Initial Conditions
The body is projected with an escape velocity, which means it has enough kinetic energy to overcome gravitational potential energy and theoretically reach infinity. The escape velocity ve is given by:
ve=√2GMeRe
where G is the gravitational constant, Me is the mass of the Earth, and Re is the radius of the Earth.
Step 2: Write the Energy Conservation Equation
At the surface of the Earth (point 0) and at height h (point 1), we can apply the conservation of mechanical energy:
E0=E1
The total mechanical energy at the surface (kinetic + potential) is:
E0=12mv2e−GMemRe
At height h, the total mechanical energy is:
E1=12mv2−GMemRe+h
Step 3: Set the Energies Equal
Setting E0 equal to E1:
12mv2e−GMemRe=12mv2−GMemRe+h
Step 4: Simplify the Equation
Cancel m from both sides (assuming m≠0) and rearranging gives:
12v2e−GMeRe=12v2−GMeRe+h
Step 5: Solve for Velocity v
Rearranging this equation allows us to express v2:
12v2=12v2e−(GMeRe−GMeRe+h)
Step 6: Calculate the Time Taken to Reach Height h
Using the relationship between velocity and displacement, we can express the time taken dt in terms of dr:
v=drdt⟹dt=drv
Substituting for v gives:
dt=dr√v2e−2GMer
Step 7: Integrate to Find Total Time
Integrate from Re to Re+h:
t=∫Re+hRedr√v2e−2GMer
This integral can be solved using standard calculus techniques. The result will yield an expression for t in terms of h.
Final Expression for Time
After performing the integration and simplifying, we arrive at the final expression for the time taken to reach height h:
t=23√R3e2g((1+hRe)3/2−1)
The body is projected with an escape velocity, which means it has enough kinetic energy to overcome gravitational potential energy and theoretically reach infinity. The escape velocity ve is given by:
At the surface of the Earth (point 0) and at height h (point 1), we can apply the conservation of mechanical energy:
Setting E0 equal to E1:
Cancel m from both sides (assuming m≠0) and rearranging gives:
Rearranging this equation allows us to express v2:
Using the relationship between velocity and displacement, we can express the time taken dt in terms of dr:
Integrate from Re to Re+h:
After performing the integration and simplifying, we arrive at the final expression for the time taken to reach height h:
Topper's Solved these Questions
Similar Questions
A body is projected vertically upward from the surface of the earth with escape velocity. Calculate the time in which it will be at a height (measured from the surface of the arth) 8 time the radius of the earth (R). Acceleration due to gravity on the surface of the earth is g.
View SolutionA body is projected vertically upwards from the surface of earth with a velocity equal to half the escape velocity. If R be the radius of earth, maximum height attained by the body from the surface of earth is Rn. Find the value of n.
View Solution
Knowledge Check
A body is projected vertically upward from the surface of the earth, then the velocity-time graph is:-
A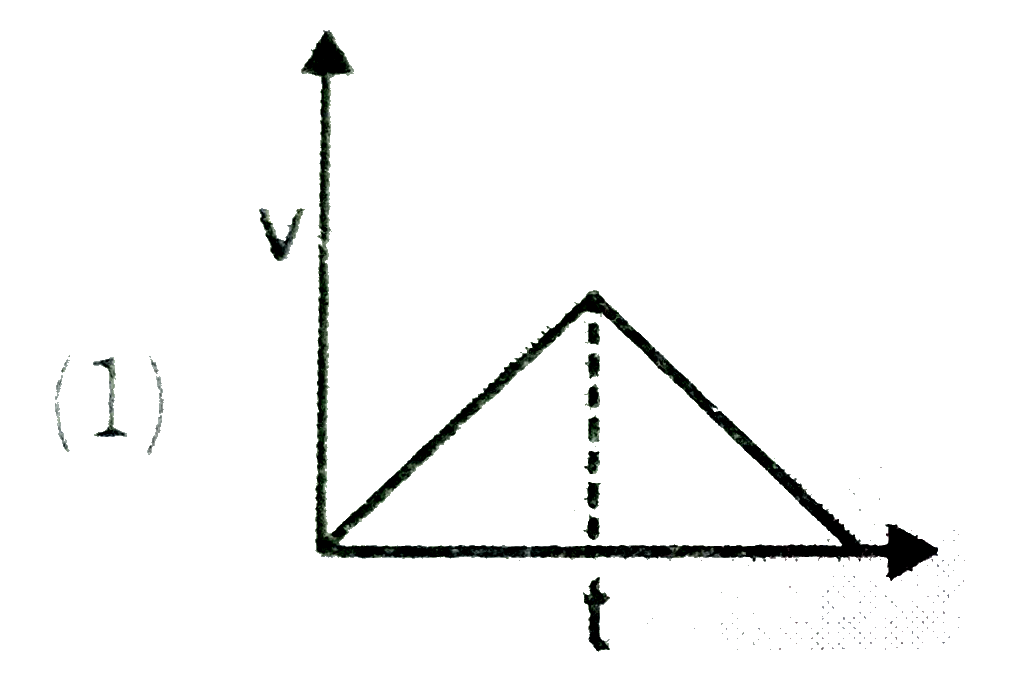 B
B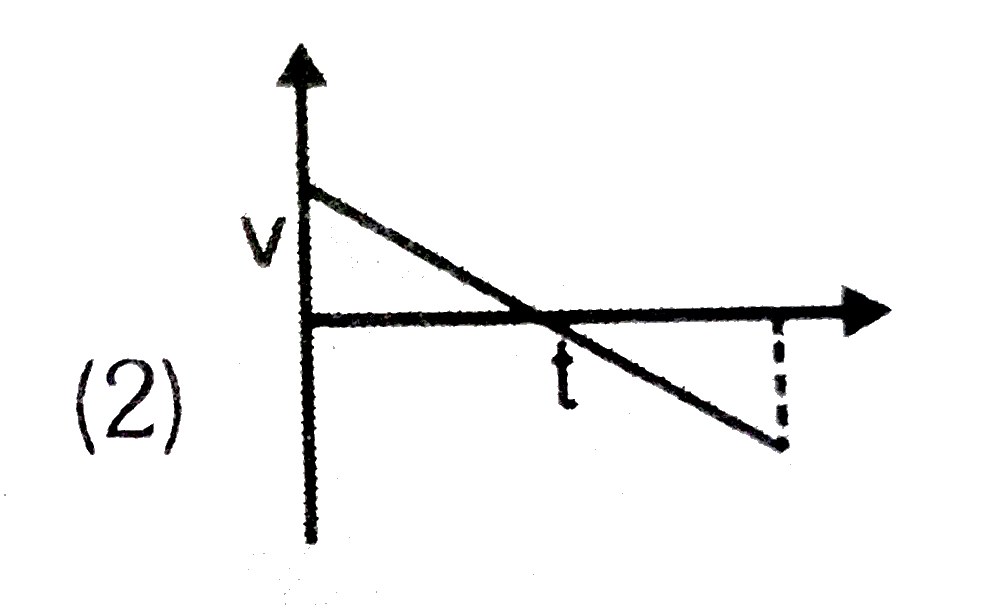 C
C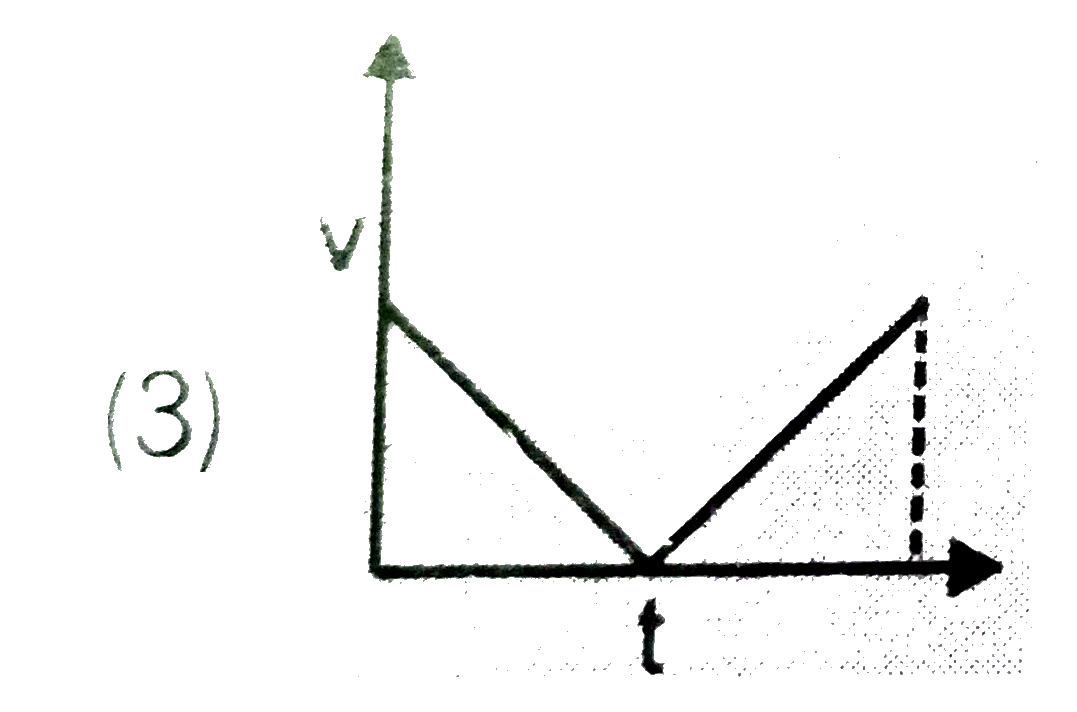 D
D
A body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to hall the escape velocity for that planet. The maximum height attained by the body is
AR/2BR/3CR/5DR/4A body is projected vertically up from surface of the earth with a velocity half of escape velocity. The ratio of its maximum height of ascent and radius of earth is
A1:1B1:2C1:3D1:4
A body is projected vertically upward from. the surface of the earth.with a velocity equal to half its escape velocity. If R is radius of the earth, then the maximum height attained by the,body is (Rn). Find n.
View SolutionAn object is projected vertically upward from the surface of the earth of mass M with a velocity such that the maximum height reached is eight times the radius R of the earth. Calculate:
(i) the initial speed of projection
(ii) the speed at half the maximum height.
View SolutionA body is projected vertically upwards from the surface of the earth with a velocity equal to half of escape velocity of the earth. If R is radius of the earth, maximum height attained by the body from the surface of the earth is
View SolutionA body is projected vertically upwards from the surface of the earth with an initial velocity v. Show that the it wall go up to a height h given by h=v2R/(2gRv2) and hence deduce the expression for escape velocity .
View SolutionA body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to 1/3rd the escape velocity for the planet. The maximum height attained by the body is
View Solution

