A narrow parallel beam of light falls on a glass sphere of radius R and refractive index at normal incidence. The distance of the image from the outer edge is given by-
The correct Answer is:A
Now
Now
Replace by and solving for
We get
First image is real and second is virtual.
Similar Questions
A horizontal ray of light is incident on a solid glass sphere of radius R and refractive index μ . What is net deviation of the beam when it emerged from the other side of the sphere?
View SolutionA parallel beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index 2.0 as shown in figure. The position of the image formed by refraction at the first surface is :

View Solution
Knowledge Check
A point object is placed at the center of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
A6cmB4cmC12cmD9cmA point object is placed at the centre of a glass sphere of radius 6cm and refractive index 1.5. The distance of virtual image from the surface is
A6cmB4cmC12cmD9cmA point object is placed at the centre of a glass sphere of radius 6 cm and refractive index 1.5. The distance of the virtual image from the surface of the glass is
A2 cmB4 cmC6 cmD12 cm
A ray of light falls on a glass plate of refractive index μ=1.5.
What is the angle of incidence of the ray if the angle between the reflected and
refracted rays is 90∘?
View SolutionA parallel incident beam falls on a solid glass sphere at near normal incidence.Show that the image in terms of the index of refractive μ and the sphere of radius R is given by
R(2−μ)2(μ−1)
View SolutionA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
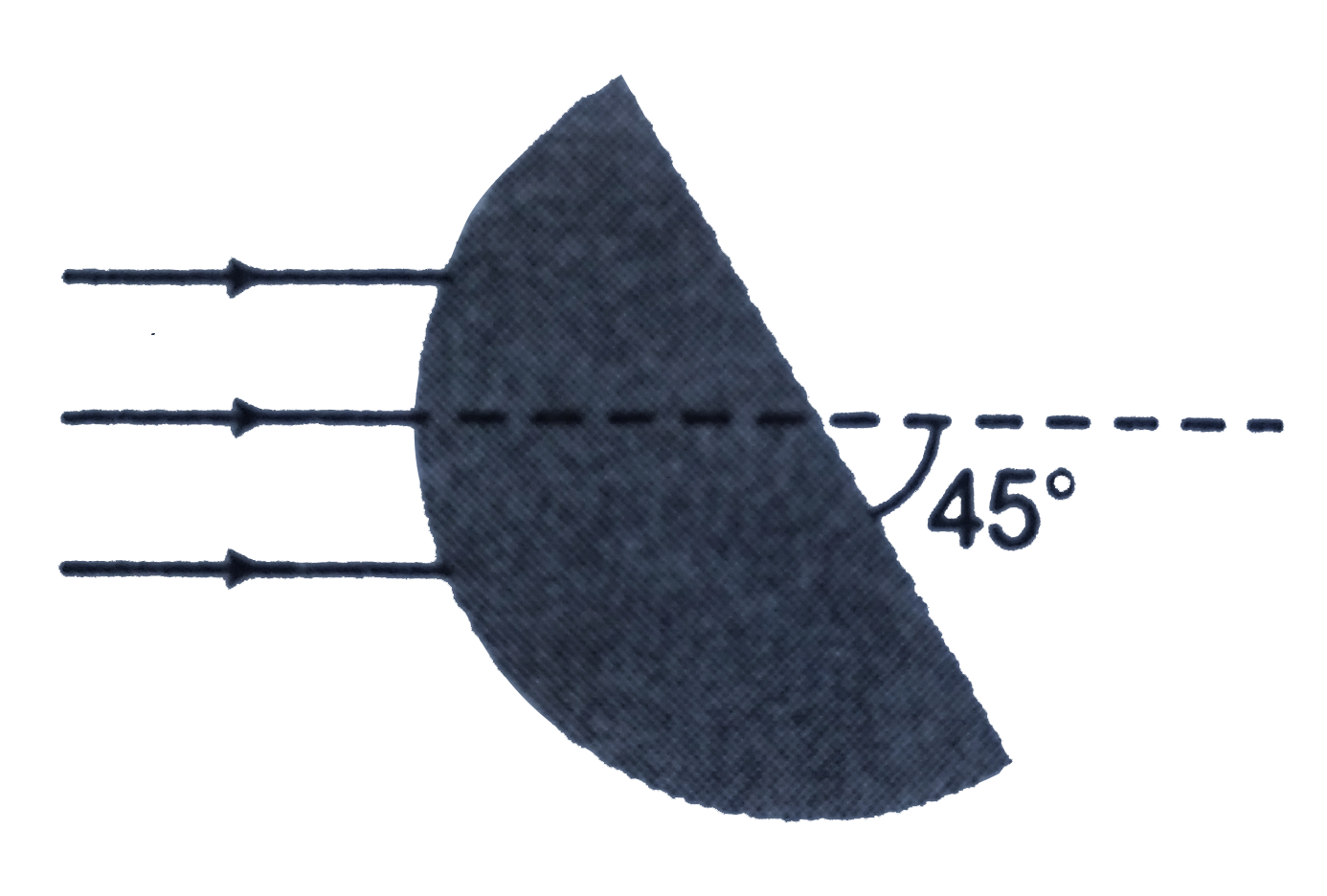
View SolutionThere is a small air bubble at the centre of a solid glass sphere of radius 'r' and refractive index μ. What wil be the apparent distance of the bubble from the centre of the sphere, when viewed from outside?
View SolutionA parallel beam of light falls on a solid tranparent sphere.

Q. For what value of refractive index μ, the thin beam can be focussed at centre of sphere.
View Solution