A parallel incident beam falls on a solid glass sphere at normal incidenc. Prove that the distance of the fianll image after two refractions is at a distance from the outer edge of the sphere. Refractive index of the sphere is and radius of the sphere is a.
Solving (i) and (ii), we get

Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Exercise1.6
Explore 15 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Exercise1.7
Explore 21 Videos
- GEOMETRICAL OPTICSBook:CENGAGE PHYSICSChapter:GEOMETRICAL OPTICSExercise:Exercise1.4
Explore 12 Videos
- FRICTIONBook:CENGAGE PHYSICSChapter:FRICTIONExercise:QUESTION BANK
Explore 1 Video
- GRAVITATIONBook:CENGAGE PHYSICSChapter:GRAVITATIONExercise:Question Bank
Explore 39 Videos
Similar Questions
A parallel incident beam falls on a solid glass sphere at near normal incidence.Show that the image in terms of the index of refractive μ and the sphere of radius R is given by
R(2−μ)2(μ−1)
View SolutionA narrow parallel beam of light falls on a glass sphere of radius R and refractive index μ at normal incidence. The distance of the image from the outer edge is given by-
View Solution
Knowledge Check
A poing source of light at the surface of a sphere causes a paralel beam of light to emerge from the opposite surface of the sphere. The refractive index of the material of the sphere is
A1.5B5/3C2D2.5A point source of light is kept on the surface of a sphere and it is found that parallel light rays emerge from the other side of the sphere. What is refractive index of material of the sphere ?
A1.5B2C2.5D3Parallel rays are incident on a transparent sphere along its one diameter. After refraction, these rays converge at the other end of this diameter. The refractive index for the material of sphere is
A1B1.5C1.6D2
A narror parallel beam of light is incident paraxially on a solid transparent sphere of radius r kept in air. What should be the refreative index if the beam is to be focusd (a) at the further surface of the sphere, (b) at the centre of the sphere.
View SolutionA narrow parallel beam of light is incident on a transparent sphere of refractives indexnif the beam finally gets focussed at a point situated at a distance=2×(radius of sphere) form the center of the sphere then findn?
View SolutionA parallel beam of light falls on a solid tranparent sphere.
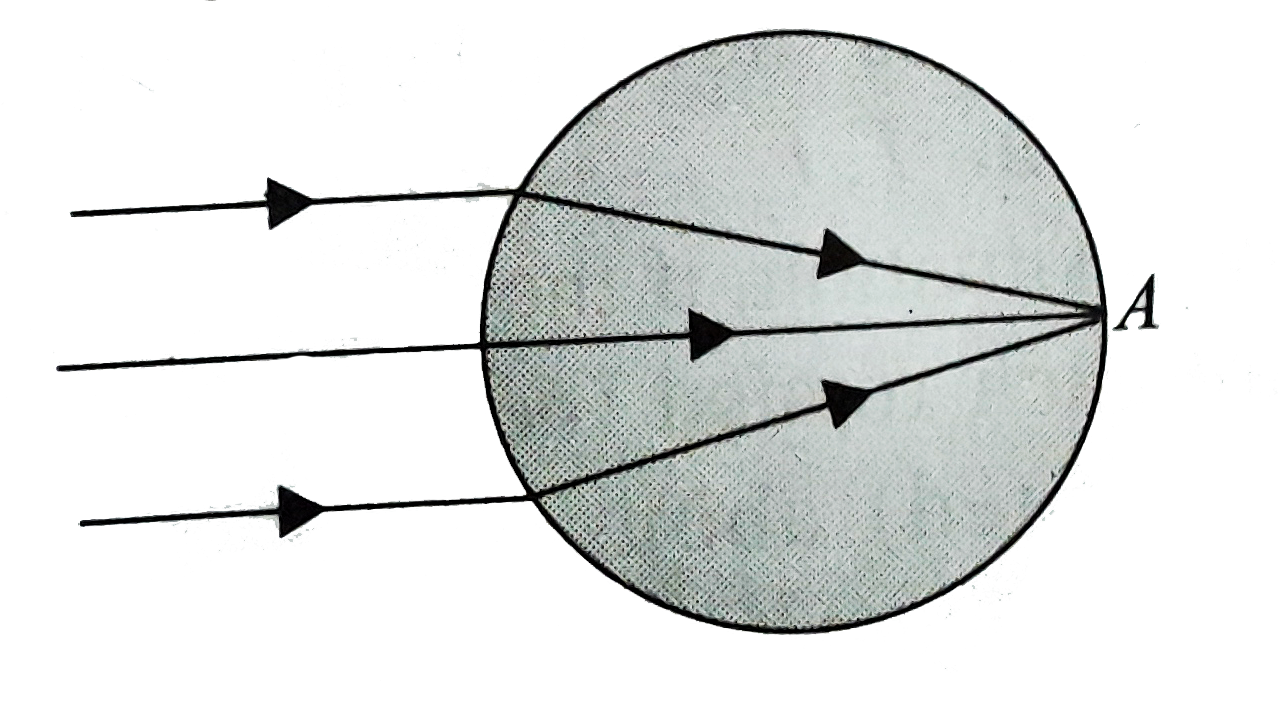
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,
View SolutionA parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
View SolutionA parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
View Solution

