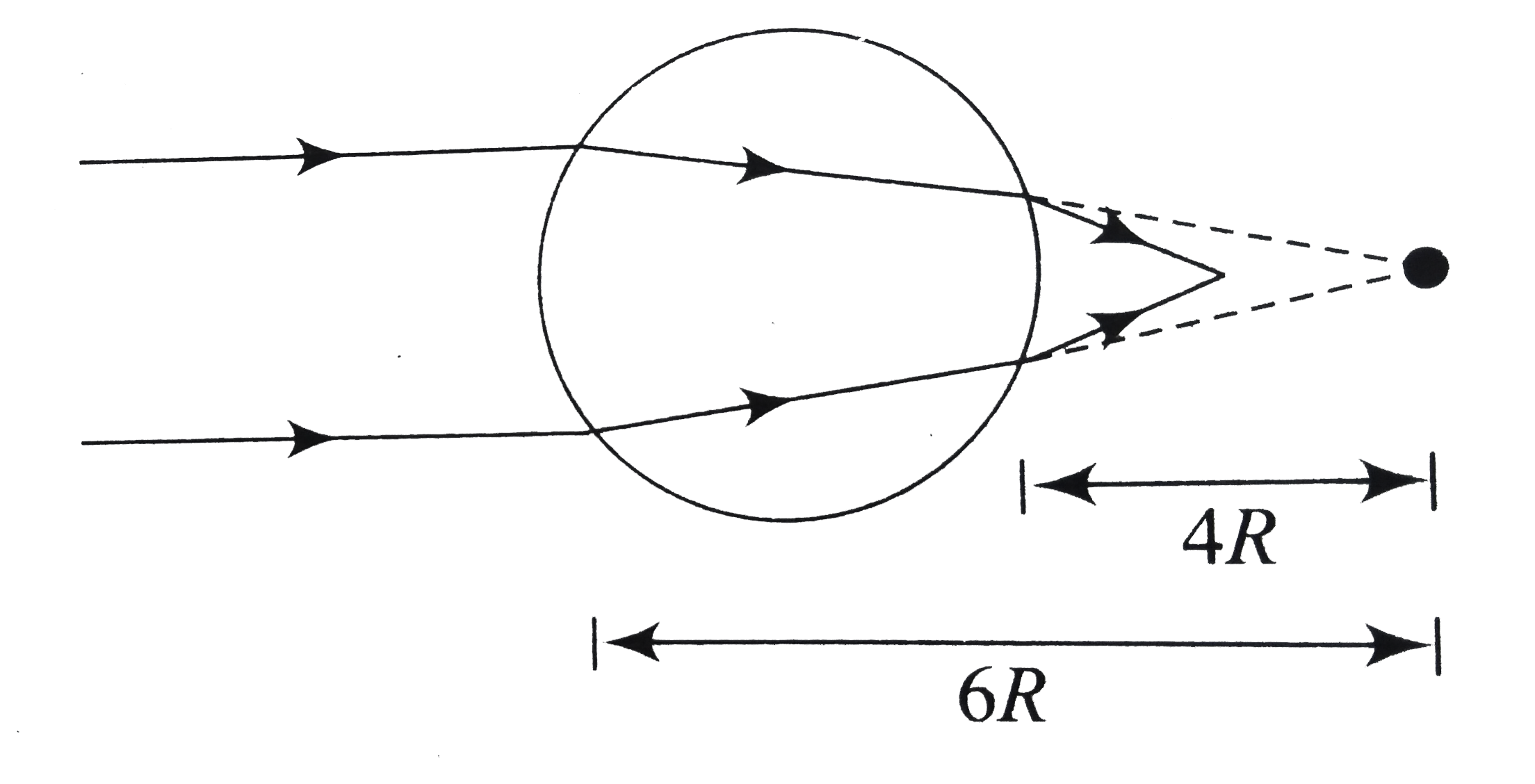
A clear transparent glass sphere (μ=1.5) of radius R is immersed in a liquid of refractive index 1.25. A parallel beam of light incident on it will converge to a point. The distance of this point from the center will be
−3R
+3R
−R
+R
The correct Answer is:b.
μ1−u+μ2v=μ2−μ1R
1.25−(∞)+1.5v=1.5−1.25R or 1.5v=0.25R
or v=1.5R0.25=6R
Again, μ2−u+μ1v=μ1−μ2R
1.5−4R+12.5v=1.25−1.5−R
or 1.25v=14R+1.54R=2.54R
=1.25×4R2.5=5R2.5
or v=2R
Distance from the center =3R
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
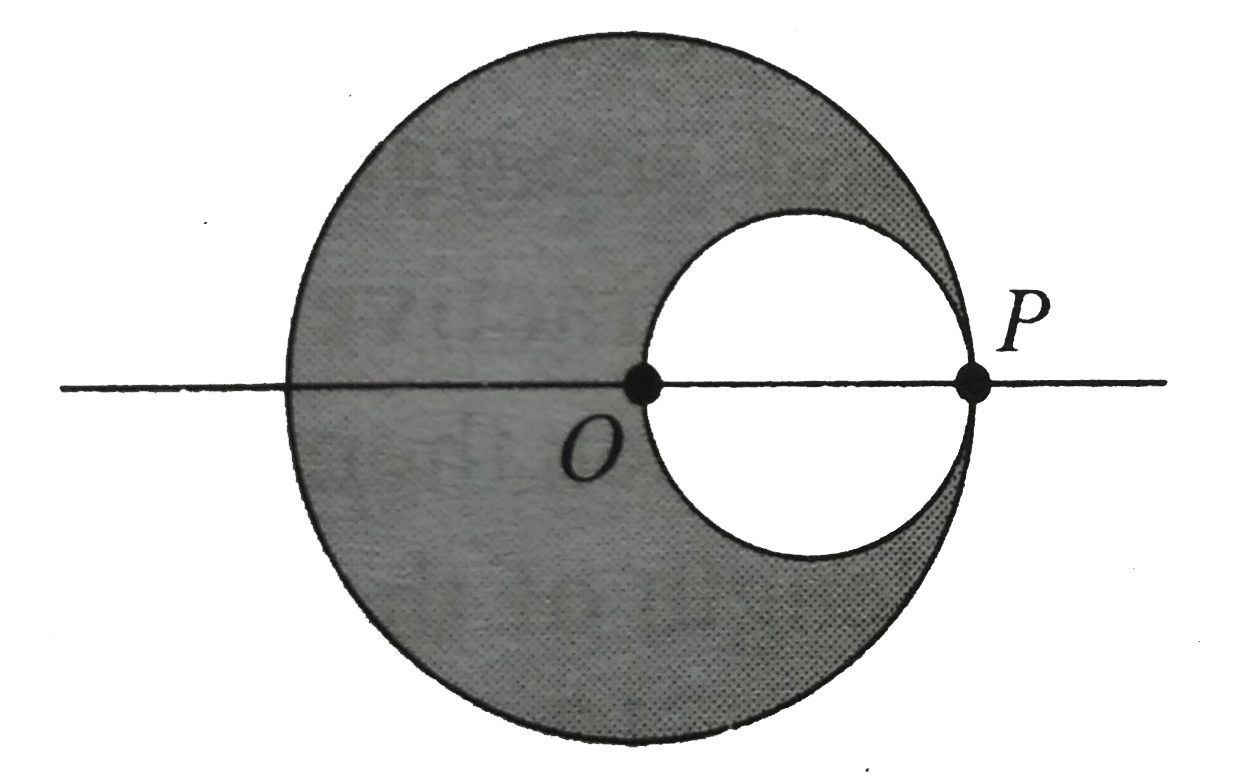
A transparent sphere of radius R ahs a cavity of radius R/2 as shown in figure,. Find the refractive index of the sphere if a parallel beam of light falling on left sureface focuses at point P.
View SolutionA lens is made of flint glass (refractive index =1.5). When the lens is immersed in a liquid of refractive index 1.25 , the focal length:
View Solution
Knowledge Check
If a small angled prism, made of glass is immersed in a liquid of refractive index 1 and a ray of light is made incident on it, then
Aits deviation will be zeroBit will suffer total reflectionCthe emergent ray is bent towards the edge of the prismDthe emergent ray is bent towards the base of prismA lens is made of flint glass (refractive index = 1.5) when the lens is immersed in a liquid of refractive index 1.25, the focal length :
AIncreases by a factor of 1.25BIncreases by a factor of 2.5CIncreases by a factor of 1.2DDecreases by a factor of 1.2A lens is made of flint glass (refractive index = 1.5) when the lens is immersed in a liquid of refractive index 1.25, the focal length :
AIncreases by a factor of 1.25BIncreases by a factor of 2.5CIncreases by a factor of 1.2DDecreases by a factor of 1.2
A lens is made of flint glass (refractive index =1.5). When the lens is immersed in a liquid of refractive index 1.25 , the focal length:
View SolutionA double convex lens of glass of refraction index μ is immersed in a medium of refractive index μ1. If a parallel beam emerges undeviated through the lens, then
View SolutionA glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach on the face BC if

View SolutionA glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach on the face BC if.

View SolutionA thin convergent glass lens (μg=1.5) has a power of +5.0D. When this lens is immersed in a liquid of refractive index μ1, it acts as a divergent lens of focal length 100cm. The value of μ1 is
View Solution
