A glass sphere, refractive index 1.5 and radius 10cm, has a spherical cavity of radius 5cm concentric with it. A narrow beam of parallel light is directed into the sphere. Find the final image and its nature.

25cm left of S4, virtual
25 cm right of S4 , real
15 cm left of S4, virtual
20cm right of S4, virtual
The correct Answer is:a.
We will have single surface refractions successsively at the four surfaces S1,S2,S3andS4. Do not forget to shift origin to the vertex of respective surface.
Refractive at first surface S1: Light travels from air to glass.
1.5υ1−1∞=(1.5−1)(+10)
υ1=30cm
First image is object for the refractioni at second surface.
For refraction at surface S2: Light travels from glass to air.
1.5υ2−1.5(+25)=1−1.5(+5)
υ2=−25cm
For refraction at surface S3: Light travels from air to glass.
1.5υ3−1(−35)=(1.5−1)(−5)
υ3=−35/3cm
For refraction at surface S4: Light travels from glass to air
1υ4−1.5−(35/3+5)=1−1.5−10
The final image is virtual, formed at 25cm to the left of the vertex of surface S4.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Assertion-Reasoninig
2 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Linked Comprehension
51 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Subjective
26 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Videos
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
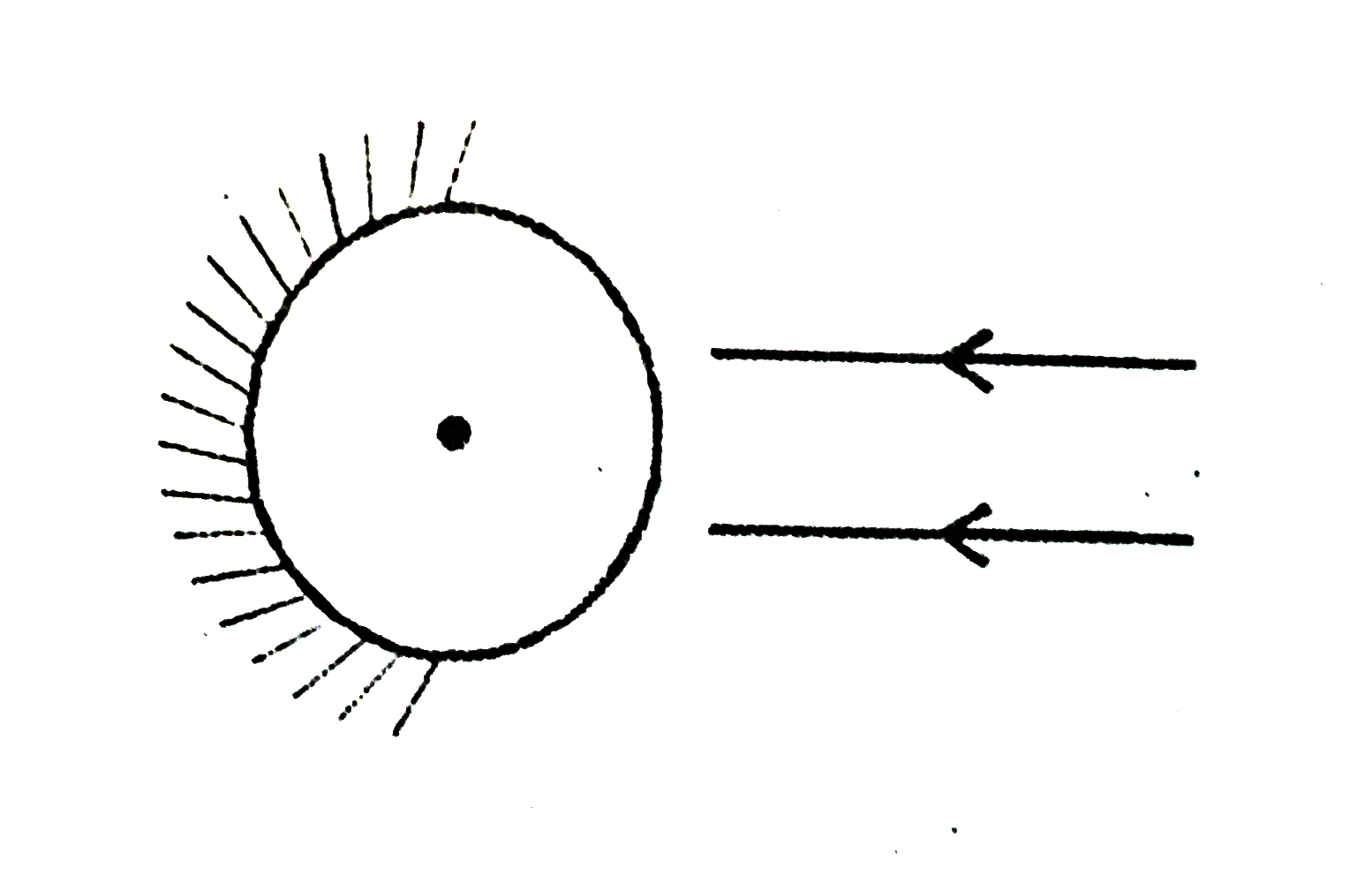
A glass sphere of index 1.5 and radius 40 cm has half its hemispherical surface silvered.
The point where a parallel beam of light, coming along a diameter, will focus (or appear to) after coming out of sphere, will be :
View SolutionFind the volume and surface area of a sphere of radius 10.5 cm.
View Solution
Knowledge Check
A glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.

Q. When viewer is on right side of the hollow sphere, what will be apparent change in position of the object?A(n−1)(3n+1)R,towards leftB(n+1)(3n−1)R,towards leftC(n+1)(3n+1)R,towards rightD(n−1)(3n+1)R,towards rightA glass sphere of radius 2R and refractive index n has a spherical cavity of radius R, concentric with it.

Q. When viewer is ono left side of the hollow sphere, what will be the shift in position of the object?A(n+1)(n−1)R,rightB(n−1)(n+1)R,rightC(2n−1)(2n+1)R,leftD2(n−1)(n+1)R,leftThe volume of a sphere of radius 10.5cm is
A9702cm3B4851cm3C19494cm3D14553cm3
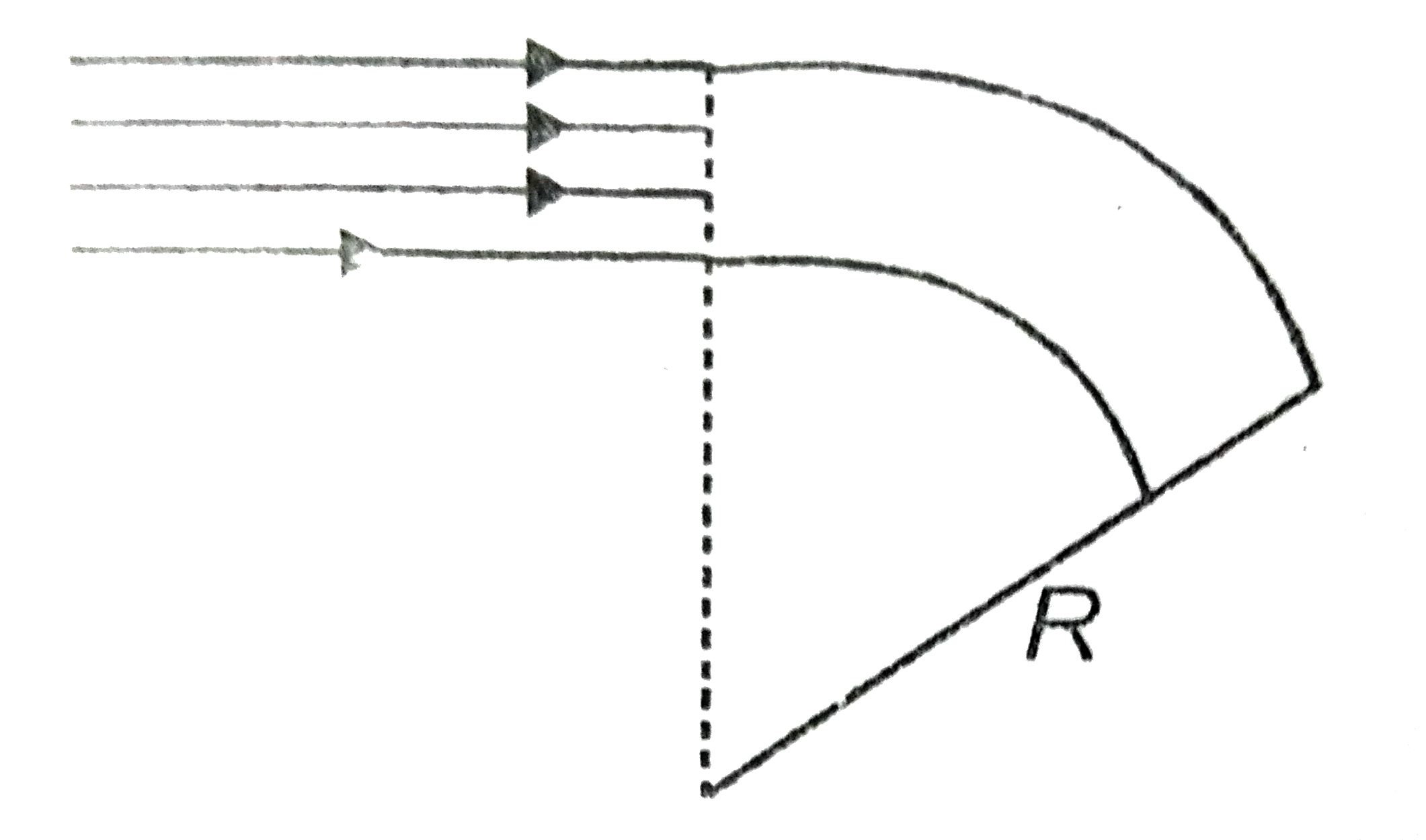
A portion of a straight glass rod of diameter 2 cm and refractive index 1.5 is bent into an arc of a circle of radius R cm and a parallel beam of light is incident on it as shown in figure. Find the smallest R which permits all the light to pass around the arc.
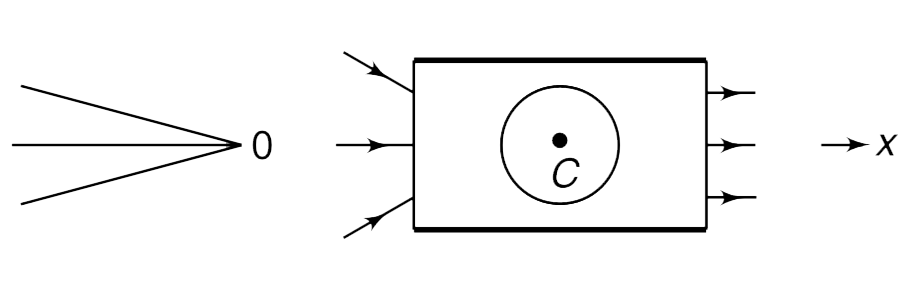
View SolutionA beam of light rays converges to a point O on x-axis as shown. The angle of convergence is small. A cube of glass of refractive index μ=1.5 and side length 40cmcontaining a concentric spherical air cavity of radius 10 cm is to be placed in the path of the converging beam so that the beam emerging from the cube is parallel to x-axis. At what point C on x-axis should the centre of the cube be placed to achieve this? Give the x coordinate of C taking O as origin.
View SolutionA ring of radius 1cm is placed 1m in front of a spherical glass ball of radius 25cm with refractive index 1.50. Determing the positiion of the final image of the ring and its magnification.
View SolutionA parallel beam of light travelling in water (refractive index =4/3) is refracted by a spherical air bublle of radius 2mm situated in water. Assuming the light rays to be paraxial,
a. Find the position of image due to refraction at first surface and position of the final image.
b. Draw a ray diagram showing the position of both images.
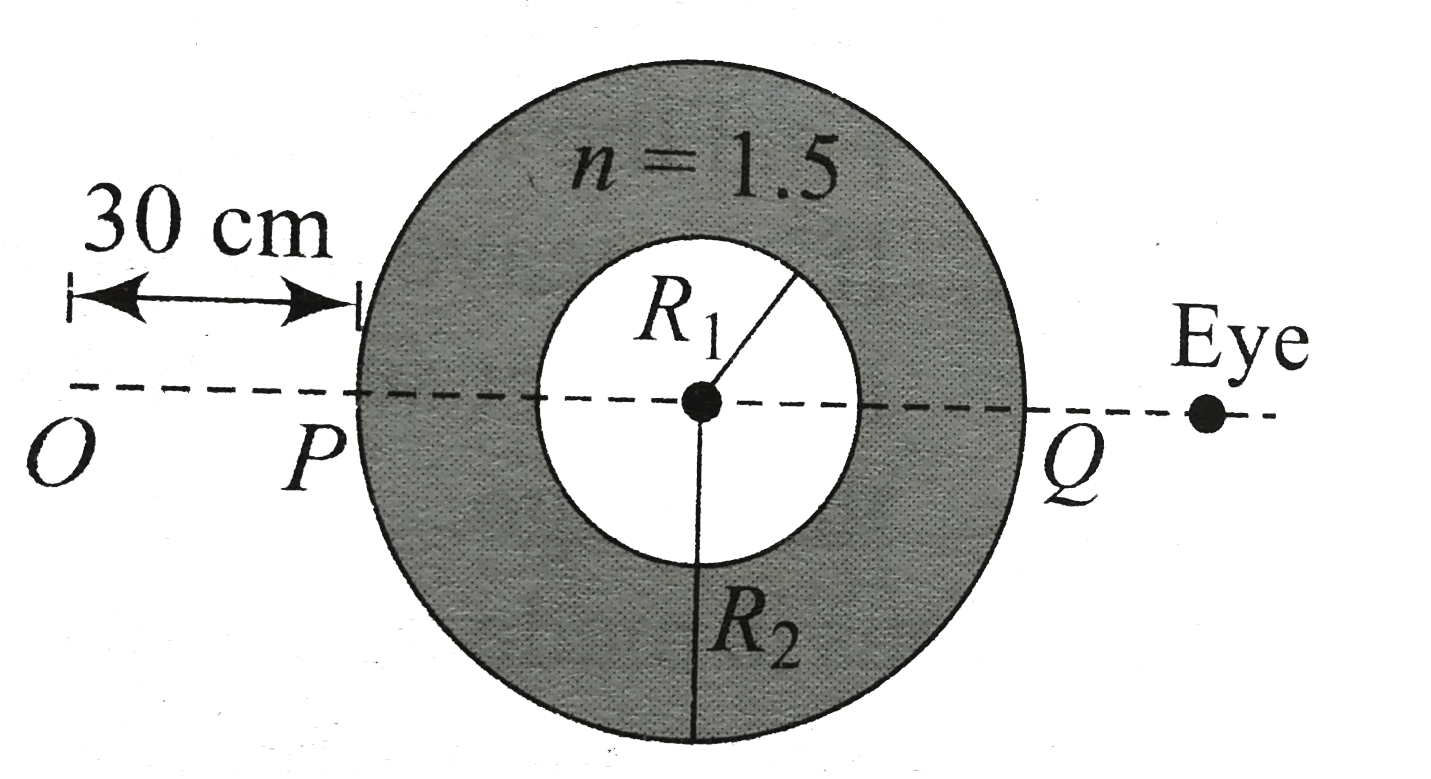
View SolutionThere is a spherical glass shell of refractive index 1.5, inner radius 10 cm and outer radius 20 cm. Inside th espherical cavity, there is air. A point object is placed at a point O at a distance of 30cm from the outer spherical surface. Find the final position of th eimage as seen eye.
View Solution
