A projectile is projected with velocity of 25 m/s at an angle with θ the horizontal. After t seconds its inclination with horizontal becomes zero. If R represents horizontal range of the projectile, the value of θ will be: [use g=10m/s2 ]
12sin−1(5t24R)
12sin−1(4R5t2)
tan−1(4t25R)
cot−1(R20t2)
The correct Answer is:C
To solve the problem, we need to find the angle θ at which a projectile is launched such that after a time t, its inclination with the horizontal becomes zero.
1. Understanding the Problem:
- A projectile is launched with an initial velocity u=25m/s at an angle θ with the horizontal.
- After time t, the projectile reaches its highest point where its vertical component of velocity becomes zero, making its inclination with the horizontal zero.
2. Vertical Motion Analysis:
- The vertical component of the initial velocity is given by:
uy=usinθ=25sinθ
- At the highest point, the vertical velocity is zero. The time taken to reach the highest point can be calculated using the formula:
t=uyg=25sinθ10=2.5sinθ
3. Time of Flight:
- The total time of flight T for the projectile is given by:
T=2usinθg=2×25sinθ10=5sinθ
- The time to reach the highest point is half of the total time of flight:
t=T2=5sinθ2
4. Equating the Two Expressions for Time:
- From the two expressions for t:
2.5sinθ=5sinθ2
- Cross multiplying gives:
5sinθ=5sinθ
- This equation is always true, meaning we need to derive the range R to find θ.
5. Horizontal Range Calculation:
- The horizontal component of the initial velocity is:
ux=ucosθ=25cosθ
- The horizontal range R can be calculated as:
R=ux⋅T=(25cosθ)⋅(5sinθ)=125sinθcosθ
- Using the identity sin(2θ)=2sinθcosθ:
R=1252sin(2θ)
6. Finding θ:
- Rearranging the range equation:
sin(2θ)=2R125
- To find θ:
2θ=sin−1(2R125)
θ=12sin−1(2R125)
7. Final Expression:
- Thus, the angle θ can be expressed in terms of the range R:
θ=12sin−1(2R125)
- A projectile is launched with an initial velocity u=25m/s at an angle θ with the horizontal.
- After time t, the projectile reaches its highest point where its vertical component of velocity becomes zero, making its inclination with the horizontal zero.
- The vertical component of the initial velocity is given by:
uy=usinθ=25sinθ
- At the highest point, the vertical velocity is zero. The time taken to reach the highest point can be calculated using the formula:
t=uyg=25sinθ10=2.5sinθ
- The total time of flight T for the projectile is given by:
T=2usinθg=2×25sinθ10=5sinθ
- The time to reach the highest point is half of the total time of flight:
t=T2=5sinθ2
- From the two expressions for t:
2.5sinθ=5sinθ2
- Cross multiplying gives:
5sinθ=5sinθ
- This equation is always true, meaning we need to derive the range R to find θ.
- The horizontal component of the initial velocity is:
ux=ucosθ=25cosθ
- The horizontal range R can be calculated as:
R=ux⋅T=(25cosθ)⋅(5sinθ)=125sinθcosθ
- Using the identity sin(2θ)=2sinθcosθ:
R=1252sin(2θ)
- Rearranging the range equation:
sin(2θ)=2R125
- To find θ:
2θ=sin−1(2R125)
θ=12sin−1(2R125)
- Thus, the angle θ can be expressed in terms of the range R:
θ=12sin−1(2R125)
Topper's Solved these Questions
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - Physics - Section B
40 Videos
- JEE MAINS 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2022EXERCISE - PHYSICS- SECTION A
19 Videos
- JEE MAINS 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2021EXERCISE - Physics (Section B )
10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINS 2023 JAN ACTUAL PAPEREXERCISE - Question
360 Videos
Similar Questions
Knowledge Check
A particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
A10mB5mC2.5mD1mA projectile is projected with a velocity u at an angle θ with the horizontal. For a fixed θ, which of the graphs shown in the following figure shows the variation of range R versus u?
A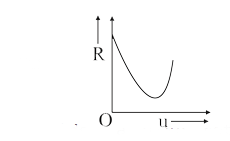 B
B C
C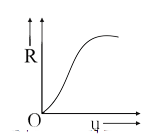 D
D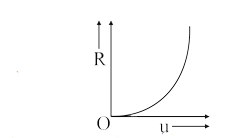
A projectile is projected with a speed u at an angle θ with the horizontal. What is the speed when its direction of motion makes an angle θ/2 with the horizontal
Aucosθ2BucosθCu(2cos(θ)2−sec(θ)2)Du(cos(θ)2−sec(θ)2)
Whe a projectile is projeected with velcity (v0 making an angle θ with the horizontal direction, then maximum horizontal range is…………………………… .
View SolutionThe direction of motion of a projectile at a certain instant is inclined at an angle 60∘ to the horizontal. After √3 seconds it is inclined an angle 30∘. If the horizontal compound of velocity of projection is 3n (in m/sec) then value of n is : (takeg=10m/s2)
View SolutionA particle is projected with a velocity of 30 m/s at an angle θ with the horizontal . Where θ=tan−1(34) . After 1 second, direction of motion of the particle makes an angle α with the horizontal then α is given by
View SolutionA projectile is projected with the initial velocity (6i+8j)m/s. The horizontal range is (g=10m/s2)
View Solutiona particle is projected down on inclined plane with a velocity of 21m/s at an angle of 60∘ with the horizontal its range on the inclined plane inclined at an angle of 30∘ with the horizontal is
View Solution

