The current density in a cylindrical wire of radius r=4 mm is 1.0×106A/m2. The current through the outer portion of the wire between radial distances r2 and r is xπ A, where x is
The correct Answer is:12
To solve the problem, we need to find the current flowing through the outer portion of the cylindrical wire between the radial distances r2 and r. Here are the steps to arrive at the solution:
Step 1: Understand the Given Data
- Radius of the wire, r=4mm=4×10−3m
- Current density, J=1.0×106A/m2
Step 2: Define the Area for Current Calculation
We need to find the current flowing through the annular region between r/2 and r. The area A of this annular region can be calculated as the difference between the area of the outer circle (radius r) and the area of the inner circle (radius r/2).
A=πr2−π(r2)2
Step 3: Calculate the Areas
Calculating the area of the outer circle:
Aouter=πr2=π(4×10−3)2=π(16×10−6)=16π×10−6m2
Calculating the area of the inner circle:
Ainner=π(r2)2=π(2×10−3)2=π(4×10−6)=4π×10−6m2
Now, subtract the inner area from the outer area:
A=Aouter−Ainner=(16π×10−6)−(4π×10−6)=12π×10−6m2
Step 4: Calculate the Current
The current I through the annular region can be calculated using the formula:
I=J⋅A
Substituting the values:
I=(1.0×106A/m2)⋅(12π×10−6m2)=12πA
Step 5: Identify x
From the problem, we know that the current through the outer portion of the wire is given as xπA. From our calculation, we found that:
I=12πA
Thus, we can identify x:
x=12
Final Answer
The value of x is 12.
---
- Radius of the wire, r=4mm=4×10−3m
- Current density, J=1.0×106A/m2
We need to find the current flowing through the annular region between r/2 and r. The area A of this annular region can be calculated as the difference between the area of the outer circle (radius r) and the area of the inner circle (radius r/2).
Calculating the area of the outer circle:
Aouter=πr2=π(4×10−3)2=π(16×10−6)=16π×10−6m2
Ainner=π(r2)2=π(2×10−3)2=π(4×10−6)=4π×10−6m2
A=Aouter−Ainner=(16π×10−6)−(4π×10−6)=12π×10−6m2
The current I through the annular region can be calculated using the formula:
I=J⋅A
Substituting the values:
I=(1.0×106A/m2)⋅(12π×10−6m2)=12πA
From the problem, we know that the current through the outer portion of the wire is given as xπA. From our calculation, we found that:
I=12πA
Thus, we can identify x:
x=12
The value of x is 12.
Topper's Solved these Questions
- JEE MAINS 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAINS 2022Exercise:PHYSICS (SECTION -A)
Explore 20 Videos
- JEE MAINS 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAINS 2021Exercise:Physics (Section B )
Explore 10 Videos
- JEE MAINS 2023 JAN ACTUAL PAPERBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINS 2023 JAN ACTUAL PAPERExercise:Question
Explore 360 Videos
Similar Questions
(a) The current density in a cylindrical wire of radius R=2.0mm is uniform across a cross section of the wire and is J=2.0×105A/m2. What is the current through the outer portion of the wire between radial distances R/2 and R?
(b) Suppose, instead, the current density through a cross section varies with radial distance r as J=ar2, in which a=3.0×1011A/m4 and r is in meters. What now is the current through the same outer portion of the wire?
View SolutionA cylindrical wire if radius R = 2 mm is of uniform area of cross-section. The current density through a cross-section varies with radial distance r as J=ar2, where a=3.2×1011A/m2 and r is in metres. What is the current through the outer portion of the wire between radial distances R/2 and R?
View Solution
Knowledge Check
The current density varies radical distance r as J=ar2, in a cylindrical wire of radius R. The current passing through the wire between radical distance R/3andR/2 is,
A65πaR42592B25πaR472C65πa2R32938DNone of theseThe current density varies radical distance r as J=ar2, in a cylindrical wire of radius R. The current passing through the wire between radical distance R/3andR/2 is,
A65πaR42592B25πaR472C65πa2R32938D81πa2R4144When a current I is set up in a wire of radius r, the drift velocity is vd. If the same current is set up through a wire of radius 2r, the drift speed will be
A0.25vdB0.5vdC2vdD4vd
The current density ¯¯¯J inside a long, solid cylindrical wire of radius a=12mm is in the direction of the central axis, and its magnitude varies linearly with radial distance r from the axis according to J=J0ra, where J0=1054πA/m2. Find the magnitude of the magnetic field at r=a2 in μT
View SolutionThe magnitude of the current density in a certain lab wire with a circular cross section of radius R=2.50 mm is given by J=(3.00×108)r2, with J in amperes per square meter and radial distance rin meters. What is the current through the outer section bounded by r= 0.900R and r=R?
View SolutionCurrent flows through a constricted conductor as shown in figure
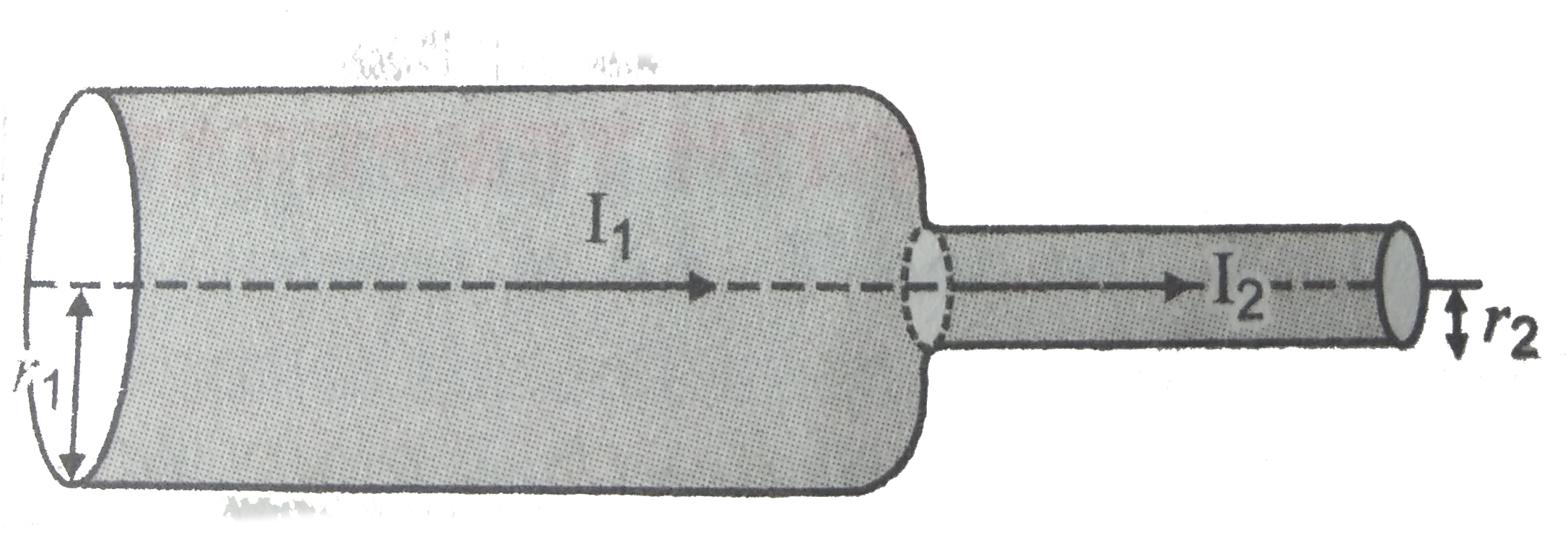
The radius and the current density to the left of constriction are 2 mm and 4.2×105Am−2. (a) How much current flows through the constriction? (b) If the current density is doubled as emerges from the right side of the constriction, what is the radius r2?
View SolutionThe current density across a cylindrical conductor of radius R varies in magnitude according to the equation J=J0(1−rR) where r is the distance from the central axis. Thus, the current density is a maximum J0 at that axis (r = 0) and decreases linearly to zero at the surface (r = R). Calculate the current in terms of J0 and the conductor 's cross - sectional area A=πR2.
View SolutionA cylindrical long wire of radius R carries a current I uniformly distributed over the cross sectional area of the wire. The magnetic field at a distance x from the surface inside the wire is
View Solution

