A projectile is projected with velocity u making angle θ with horizontal direction, find : horizontal range.
To find the horizontal range R of a projectile projected with an initial velocity u at an angle θ with the horizontal, we can follow these steps:
Step 1: Determine the Components of the Initial Velocity
The initial velocity u can be resolved into two components:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
Step 2: Calculate the Time of Flight
The time of flight T for a projectile is given by the formula:
T=2uyg
Substituting uy:
T=2(usinθ)g
Step 3: Calculate the Horizontal Range
The horizontal range R can be calculated using the formula:
R=ux⋅T
Substituting ux and T:
R=(ucosθ)⋅(2(usinθ)g)
This simplifies to:
R=2u2sinθcosθg
Step 4: Use the Trigonometric Identity
Using the identity sin2θ=2sinθcosθ, we can further simplify the range formula:
R=u2sin2θg
Final Result
Thus, the horizontal range R of the projectile is given by:
R=u2sin2θg
---
The initial velocity u can be resolved into two components:
- Horizontal component: ux=ucosθ
- Vertical component: uy=usinθ
The time of flight T for a projectile is given by the formula:
T=2uyg
Substituting uy:
T=2(usinθ)g
The horizontal range R can be calculated using the formula:
R=ux⋅T
Substituting ux and T:
R=(ucosθ)⋅(2(usinθ)g)
This simplifies to:
R=2u2sinθcosθg
Using the identity sin2θ=2sinθcosθ, we can further simplify the range formula:
R=u2sin2θg
Thus, the horizontal range R of the projectile is given by:
R=u2sin2θg
Topper's Solved these Questions
Similar Questions
Knowledge Check
A projectile is thrown with velocity u making an angle θ with the horizontal. Its time of flight on the horizontal ground is 4 second. The projectile is moving at angle of 45∘ with the horizontal just one second after the projection. Hence the angle θ is (take g=10m/s2)
Atan−1(4)B60∘C53∘Dtan−1(2)A projectile is projected with a velocity u at an angle θ with the horizontal. For a fixed θ, which of the graphs shown in the following figure shows the variation of range R versus u?
A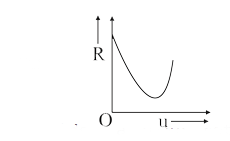 B
B C
C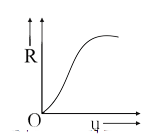 D
D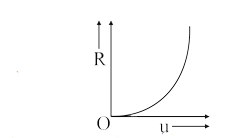
A particle is projected with a velocity u making an angle θ with the horizontal. At any instant its velocity becomes v which is perpendicular to the initial velocity u. Then v is
AucosθButanθCusecθDucotθ
For a projectile first with velocity u at an angle θ with the horizontal.

View SolutionFind (a) time of flight , (b) Max.height (c ) Horizontal range of projectile projected with speed (v) making an angle θ with the horizontal direction from ground.
View SolutionA projectile is projected from horizontal with velocity (u) making an angle 45∘ with the horizontal direction. Find the distance of the highest point of the projectile from its starting point.
View SolutionA particle is projected from the ground with velocity u at angle θ with horizontal.The horizontal range,maximum height and time of flight are R,H and T respectively.Now keeping u as fixed, θ is varied from 30∘ to 60∘.Then
View SolutionA particle is projected with a velocity u making an angle θ with the horizontal. The instantaneous power of the gravitational force
View Solution

