A projectile is projected with the initial velocity (6i+8j)m/s. The horizontal range is (g=10m/s2)
96m
960m
9.6m
4.8m
The correct Answer is:C
To solve the problem of finding the horizontal range of a projectile projected with an initial velocity of (6i+8j)m/s, we can follow these steps:
Step 1: Identify the components of the initial velocity
The initial velocity vector is given as:
→u=6^i+8^jm/s
From this, we can identify:
- The horizontal component ux=6m/s
- The vertical component uy=8m/s
Step 2: Calculate the magnitude of the initial velocity
The magnitude of the initial velocity u can be calculated using the Pythagorean theorem:
u=√u2x+u2y=√62+82=√36+64=√100=10m/s
Step 3: Calculate the angle of projection
The angle of projection θ can be found using the trigonometric ratios:
tanθ=uyux=86
To find θ:
θ=tan−1(86)=tan−1(43)
Step 4: Use the range formula
The formula for the horizontal range R of a projectile is given by:
R=u2sin2θg
Where g=10m/s2. We need to calculate sin2θ:
sin2θ=2sinθcosθ
From the components, we can find:
sinθ=uyu=810=0.8
cosθ=uxu=610=0.6
Now, substituting these values:
sin2θ=2⋅0.8⋅0.6=0.96
Step 5: Substitute values into the range formula
Now we can substitute u, sin2θ, and g into the range formula:
R=102⋅0.9610=100⋅0.9610=9.6m
Conclusion
The horizontal range of the projectile is:
9.6m
---
The initial velocity vector is given as:
→u=6^i+8^jm/s
From this, we can identify:
- The horizontal component ux=6m/s
- The vertical component uy=8m/s
The magnitude of the initial velocity u can be calculated using the Pythagorean theorem:
u=√u2x+u2y=√62+82=√36+64=√100=10m/s
The angle of projection θ can be found using the trigonometric ratios:
tanθ=uyux=86
To find θ:
θ=tan−1(86)=tan−1(43)
The formula for the horizontal range R of a projectile is given by:
R=u2sin2θg
Where g=10m/s2. We need to calculate sin2θ:
sin2θ=2sinθcosθ
From the components, we can find:
sinθ=uyu=810=0.8
cosθ=uxu=610=0.6
Now, substituting these values:
sin2θ=2⋅0.8⋅0.6=0.96
Now we can substitute u, sin2θ, and g into the range formula:
R=102⋅0.9610=100⋅0.9610=9.6m
The horizontal range of the projectile is:
9.6m
Topper's Solved these Questions
Similar Questions
What are the two angles of projection of a projectile projected with velocity of 30m/s, so that the horizontal range is 45m. Take, g=10m/s2.
View SolutionWhat are the angles of projection of a projectile projected with velocity 30ms−1, so that the horizontal range is 45 m ? Take g=10ms−2.
View Solution
Knowledge Check
A body is projected with a initial velocity of (8ˆi+6ˆj)ms−1 . The horizontal range is (g=10ms−2)
A9.6 mB14 mC50 mD100 mA projectile is thrown with an initial velocity of (x→i+y→j)m/s . If the range of the projectile is double the maximum height reached by it, then
Ax−2yBy=2xCx=yDy=4xA particle is projected with velocity of 10ms at an angle of 15° with horizontal.The horizontal range will be(g=10ms2)
A10mB5mC2.5mD1m
A particle is projected with velocity 20√2m/s at 45∘ with horizontal. After 1s(g=10m/s2) match the following table
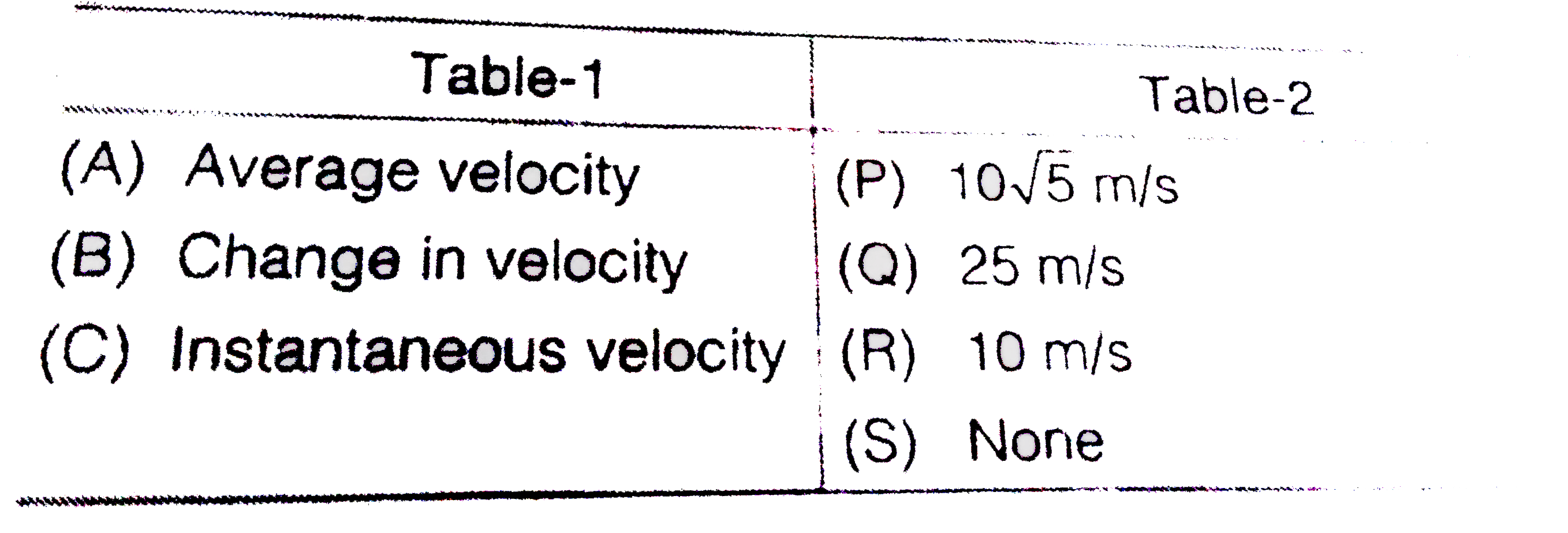
View SolutionA projectile is projected from top of a wall 20m height with a speed of 10m/s horizontally. Find range (g=10ms2)
View SolutionA projectile is projected with initial velocity (6ˆi+8ˆj) m/s.Minimum time after which its velocity becomes parallel to the line 4y-3x+2=0, is ?(¯g=−10ˆjm/s2)
View SolutionA projectile is projected in air with initial velocity →v=(3ˆi+4ˆj) m/s from the origin. The equation of trajectory of the projectile is given as (g=−10ˆjms2) (neglect air resistance )
View SolutionA projectile is projected from ground with an initial velocity (5ˆi+10ˆj)m/s If the range of projectile is R m, time of flight is Ts and maximum height attained above ground is Hm, find the numerical value of R×HT. [Take g=10m/s2]
View Solution

