A projectile is fired at an angle of 45∘ with the horizontal. Elevation angle of the projection at its highest point as seen from the point of projection is
tan−1(√32)
45∘
60∘
tan−1(12)
The correct Answer is:D
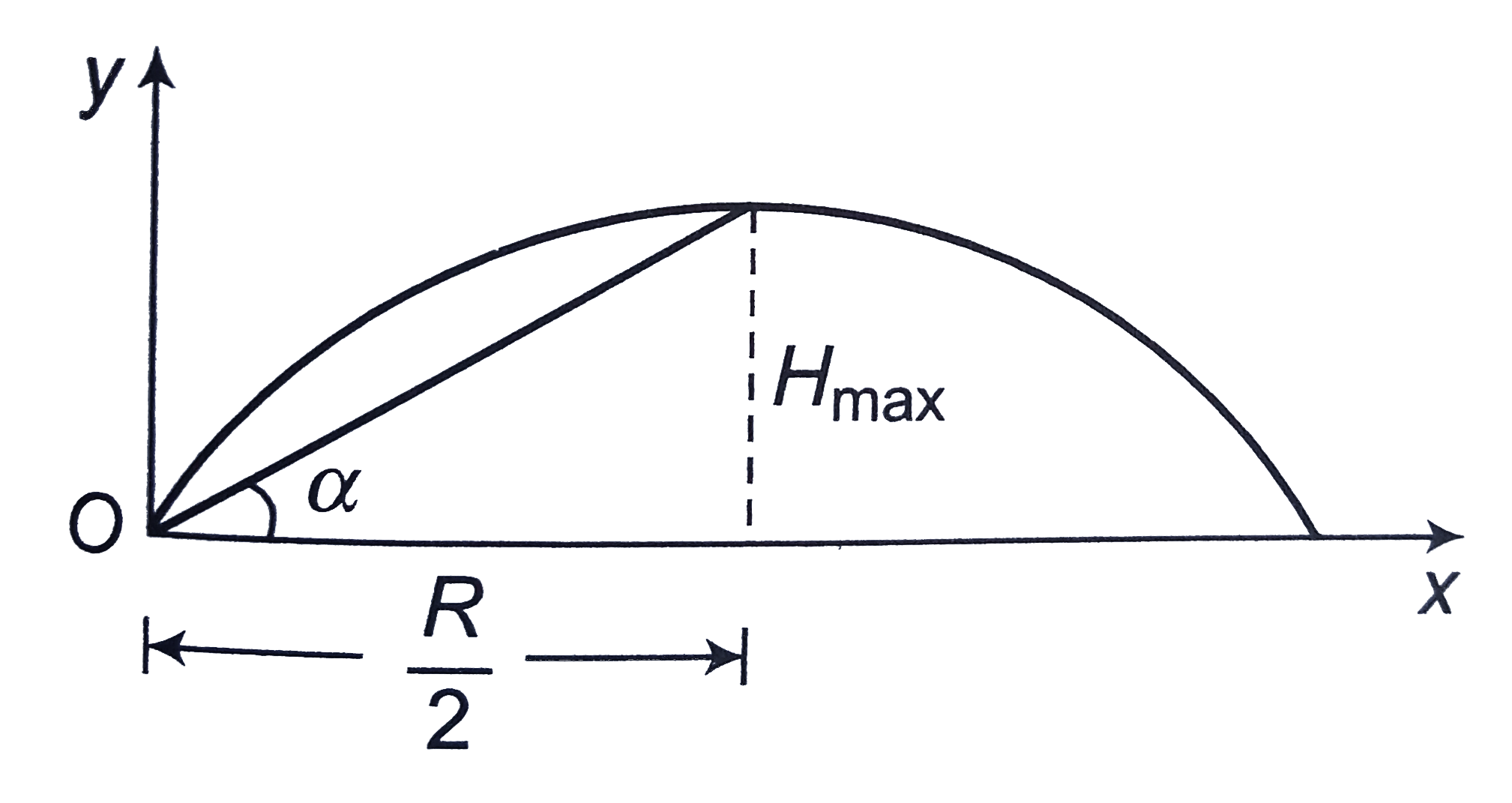
tanα=HmaxR/2=u2sin2θ/2gu2.2sinθcosθ/2g
=tanθ2=tan45∘2=12
α=tan−1(1/2)
Topper's Solved these Questions
Similar Questions
Knowledge Check
A projectile is fired from level ground at an angle θ above the horizontal. The elevation angle ϕ of the highest point as seen from the launch point is related to θ by the relation.
Atanϕ=2tanθBtanϕ=tanθCtanϕ=12tanθDtanϕ=14tanθA particle is projected at an angle θ with the horizontal . If angle of elevation of highest point of trajectory is ϕ when seen from point of projection, then
Atanϕ=2tanϕBtanθ=3tanϕCtanθ=2tanϕDtanθ=4tanϕA ball is projected with 20√2m/s at angle 45∘ with horizontal.The angular velocity of the particle at highest point of its journey about point of projection is
A0.1rad/sB1rad/sC0.3rad/sD0.4rad/s
projectile is fired from ground at an angle θ with horizontal. The elevation angle ϕ of heighest point as seen from launch point is related by the relation-
View SolutionA particle of mass 1kg is projected with an initial velocity 10ms−1 at an angle of projection 45∘ with the horizontal. The average torque acting on the projectile and the time at which it strikes the ground about the point of projection in newton meter is
View SolutionA particle is projected at 60(∘) to the horizontal with a kinetic energy K . The kinetic energy at the highest point is
View SolutionA particle of mass m is projected with a velocity v making an angle of 45∘ with the horizontal. The magnitude of the angular momentum of the projectile abut the point of projection when the particle is at its maximum height h is.
View SolutionA ball is projected at an angle 45∘ with horizontal. It passes through a wall of height h at horizontal distance d1 from the point of projection and strikes the ground at a horizontal distance (d1+d2) from the point of projection, then
View Solution
