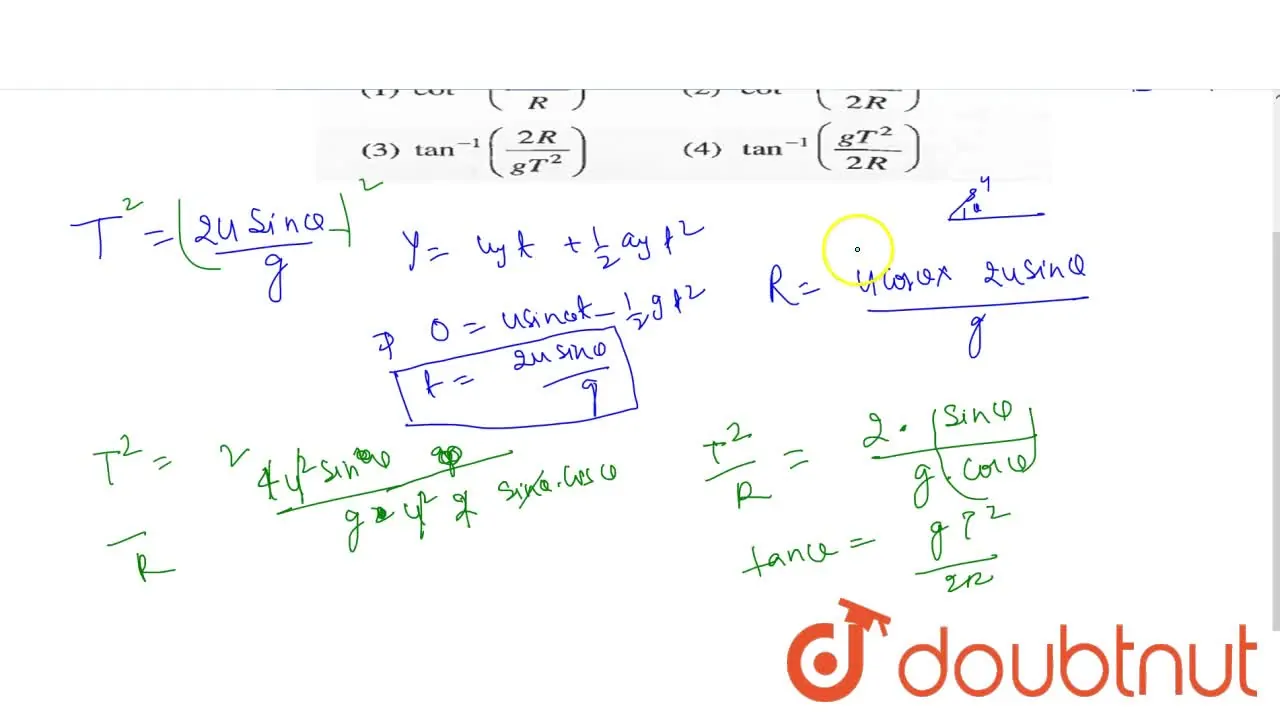
A particle is projected at an angle with horizontal. If T is the time of flight and R is a horizontal range, then θ is
cot−1(gT2R)
cot−1(gT22R)
tan−1(2RgT2)
tan−1(gT22R)
The correct Answer is:D
T=2usinθg,R=u2g.2sinθcosθ
T2R=4u2sin2θ/g22u2sinθcosθ/g=2tanθg
tanθ=gT22R⇒θ=tan−1(gT22R)
Related Playlists
Similar Questions
A particle is projected up an inclines plane. Plane is inclined at an angle θ with horizontal and particle is projected at an angle α with horizontal. If particle strikes the plane horizontally prove that tanα=2tanθ
View SolutionA projectile is projected with velocity u making angle θ with horizontal direction, find : horizontal range.
View SolutionA ball is thrown at an angle θ with the horizontal. Its time of flight is 2 s. Its horizontal range is 100 m. What is the horizontal component of velocity of projection ? Take g=10ms−2.
View SolutionIf a body is projected with an angle θ to the horizontal, then
View SolutionWhen a particle is projected at an angle to the horizontal, it has range R and time of flight t1. If the same projectile is projected with same speed at another angle to have the saem range, time of flight is t2. Show that:
t1t2=(2R/g)View SolutionA body projected at an angle with the horizontal has a range 300 m. the time of flight is 6s, then the horizontal component of velocity is
View SolutionA particle is projected at an angle θ with the horizontal . If angle of elevation of highest point of trajectory is ϕ when seen from point of projection, then
View SolutionA body is projected at an angle θ with the horizontal. Derive an expression for its horizontal range. Show that there are two angles θ1 and θ2 projections for the same horizontal range, such that θ1+θ2=90∘.
View SolutionA particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
View SolutionA particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
View Solution