A particle is projected at an angle θ=30∘ with the horizontal, with a velocity of 10ms−1. Then
After 2 s, the velocity of particle makes an angle of 60∘ with initial velocity vector.
After 1 s, the velocity of particles makes an angle of 60∘ with initial velocity vector.
The magnitude of velocity of particle after 1 s is 10ms−1.
The magnitude of velocity of particle after 1 s is 5ms−1.
The correct Answer is:B, C
To solve the problem of a particle projected at an angle of θ=30∘ with an initial velocity of 10m/s, we will calculate the velocity of the particle after 1 second and 2 seconds, as well as the angle of the velocity vector at those times.
Step 1: Resolve the initial velocity into components
The initial velocity u can be resolved into horizontal and vertical components:
- ux=ucosθ=10cos30∘=10×√32=5√3m/s
- uy=usinθ=10sin30∘=10×12=5m/s
Step 2: Calculate the vertical velocity after 1 second
The vertical component of the velocity after time t is given by:
vy=uy−gt
where g is the acceleration due to gravity (g≈9.81m/s2).
For t=1s:
vy=5−9.81×1=5−9.81=−4.81m/s
Step 3: Calculate the vertical velocity after 2 seconds
For t=2s:
vy=5−9.81×2=5−19.62=−14.62m/s
Step 4: Calculate the total velocity after 1 second
The total velocity v after 1 second can be calculated using the Pythagorean theorem:
v=√u2x+v2y
v=√(5√3)2+(−4.81)2
v=√75+23.1361=√98.1361≈9.9m/s
Step 5: Calculate the angle of the velocity vector after 1 second
The angle ϕ of the velocity vector with respect to the horizontal can be found using:
tanϕ=vyux
tanϕ=−4.815√3
Calculating ϕ:
ϕ=tan−1(−4.815√3)
This will give an angle in the fourth quadrant (since vy is negative).
Step 6: Calculate the total velocity after 2 seconds
Using the same method as in Step 4:
v=√(5√3)2+(−14.62)2
v=√75+214.4644=√289.4644≈17.0m/s
Step 7: Calculate the angle of the velocity vector after 2 seconds
Using the same method as in Step 5:
tanϕ=−14.625√3
Calculating ϕ:
ϕ=tan−1(−14.625√3)
Summary of Results
- After 1 second:
- Velocity: ≈9.9m/s
- Angle: ϕ (calculated based on the above steps)
- After 2 seconds:
- Velocity: ≈17.0m/s
- Angle: ϕ (calculated based on the above steps)
The initial velocity u can be resolved into horizontal and vertical components:
- ux=ucosθ=10cos30∘=10×√32=5√3m/s
- uy=usinθ=10sin30∘=10×12=5m/s
The vertical component of the velocity after time t is given by:
vy=uy−gt
where g is the acceleration due to gravity (g≈9.81m/s2).
For t=1s:
vy=5−9.81×1=5−9.81=−4.81m/s
For t=2s:
vy=5−9.81×2=5−19.62=−14.62m/s
The total velocity v after 1 second can be calculated using the Pythagorean theorem:
v=√u2x+v2y
v=√(5√3)2+(−4.81)2
v=√75+23.1361=√98.1361≈9.9m/s
The angle ϕ of the velocity vector with respect to the horizontal can be found using:
tanϕ=vyux
tanϕ=−4.815√3
Calculating ϕ:
ϕ=tan−1(−4.815√3)
This will give an angle in the fourth quadrant (since vy is negative).
Using the same method as in Step 4:
v=√(5√3)2+(−14.62)2
v=√75+214.4644=√289.4644≈17.0m/s
Using the same method as in Step 5:
tanϕ=−14.625√3
Calculating ϕ:
ϕ=tan−1(−14.625√3)
- After 1 second:
- Velocity: ≈9.9m/s
- Angle: ϕ (calculated based on the above steps)
- After 2 seconds:
- Velocity: ≈17.0m/s
- Angle: ϕ (calculated based on the above steps)
Topper's Solved these Questions
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Linked Comprehension Type
35 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Integer Type
17 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICSCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct Answer Type
9 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A particle of mass 1 kg is projected at an angle of 30∘ with horizontal with velocity v = 40 m/s . The change in linear momentum of the particle after time t = 1 s will be (g = 10 m/s2)
View SolutionWhat is the radius of curvature of the parabola traced out by the projectile in which a particle is projected with a speed u at an angle θ with the horizontal, at a point where the velocity of particle makes an angle θ/2 with the horizontal.
View Solution
Knowledge Check
A body is projected at an angle of 30∘ with the horizontal and with a speed of 30ms−1. What is the angle with the horizontal after 1.5 second? (g=10ms−2)
A0∘B30∘C60∘D90∘A body is projected at an angle of 30∘ with the horizontal and with a speed of 30ms−1. What is the angle with the horizontal after 1.5s ? (g=10ms−2).
A0∘B30∘C60∘D90∘A particle is projected at an angle of 60∘ above the horizontal with a speed of 10m/s. After some time the direction of its velocity makes an angle of 30∘ above the horizontal. The speed of the particle at this instant is s
A5√3m/sB5√3m/sC5m/sD10√3m/s
A projectile is projected in the upward direction making an angle of 45∘ with horizontal direction with a velocity of 150ms−1. Then the time after which its inclination with the horizontal is 30∘ is (g=10 ms^(-2)).
View SolutionA particle of mass 1kg is projected at an angle of θ=π/4 from horizontal with a muzzle velocity of 20m/s. A long slender rod of mass 5kg and length 30m is suspended vertically from a point at the same horizontal leves as that of point of projection and at a distance of 60m from the projection point. The rod can rotate freely. If collision occurs, it is perfectly plastic. (g=10m/s2)
If the rod tilts to an angle θ after collision, then
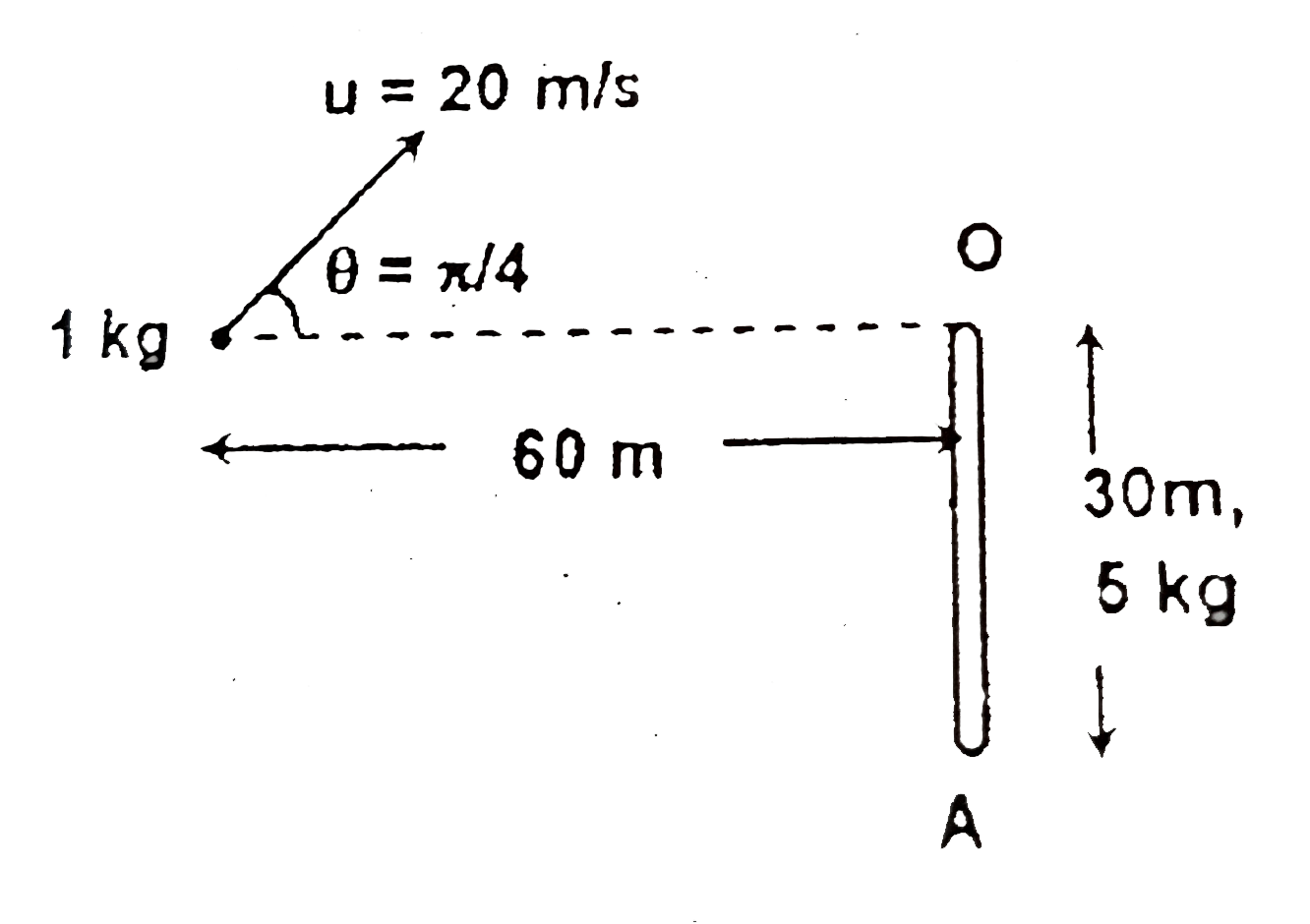
View SolutionA body is projected at angle 30∘ to horizontal with a velocity 50ms−1.Its time of flight is
View SolutionA particle is projected at an angle θ with the horizontal . If angle of elevation of highest point of trajectory is ϕ when seen from point of projection, then
View SolutionA particle is projected from horizontal making an angle of 53∘ with initial velocity 100ms−1. The time taken by the particle to make angle 45∘ from horizontal is
View Solution
