A rod of mass 'M' and length '2L' is suspended at its middle by a wire. It exhibits torsional oscillations, if two masses each of 'm' are attached at distance'L/2' from its centre on both sides, it reduces the oscillation frequency by 20%. The value of ratio m/M is close to :
0.57
0.17
0.77
0.37
The correct Answer is:D

f0=12π√cI0
f0=12π√3cML2 .............(i)
I.=ML23+2.mL24
f.=12π
⎷cL2(M3+m2)=0.8f0............(ii)
From equation (i) and (ii)
mM=924=38=0.375
Similar Questions
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is

View Solutionद्रव्यमान M तथा लम्बाई 2L की एक छड़ को उसके मध्य बिन्दु से एक तार द्वारा लटकाया गया है। यह छड़ मरोड़ दोलन करती है। यदि प्रत्येक द्रव्यमान के दो पिण्डो को छड़ के मध्य-बिन्दु से L2 दूरी पर दोनों तरफ जोड़ते है, तो दोलन की आवृत्ति 20% घट जाती है। अनुपात m/M का सन्निकट मान होगा
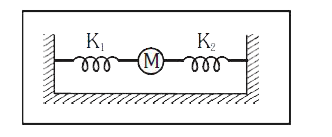
View Solutionसंलग्न चित्र में द्रव्यमान M के लिए दोलन आवृति समानुपाती होगी:
View SolutionA uniform disc of mass m and radius r is suspended through a wire attached to its Centre. If the time period of the torsional oscillations be T, what is the torsional constant of the wire?
View SolutionA rod of mass 'M' and length '2L' is suspended at its middle by a wire. It exhibits torsional oscillations, if two masses each of 'm' are attached at distance'L/2' from its centre on both sides, it reduces the oscillation frequency by 20%. The value of ratio m/M is close to :
View SolutionA mass m is suspended from a spring. Its frequency of oscillation is f. The spring is cut into two halves and the same mass is suspended from one of the pieces of the spring. The frequency of oscillation of the mass will be
View SolutionA spring elongated by length 'L' when a mass 'M' is suspended to it. Now a tiny mass 'm' is attached and then released, its time period of oscillation is -
View SolutionA rigid rod of mass m with a ball of mass M attached to the free end is restrained to oscillate in a vertical plane as shown in the figure. Find the natural frequency of oscillation.

View Solution