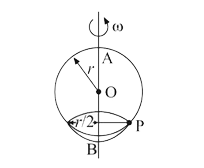
A smooth wire of length 2πr is bent into a circle and kept in a vertical plane. A bead can slide smoothly on the wire. When the circle is rotating with angular speed about the vertical diameter AB, as shown in the figure, the bead is at rest with respect to the circular ring at potion P as shown. Then the value of ω2 is equal to:
2gr
√3g2r
(g√3)r
2gr√3
The correct Answer is:D
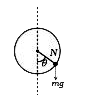
θ=30∘
Nsin30∘=mω2r2
Ncos30∘=mg
tan30∘=ω2r2g
implies ω2=2gr√3
Similar Questions
2πr लम्बाई के एक घर्षण रहित तार को वृत्त बनाकर ऊर्ध्वाधर समतल में रखा है। एक मणिका (bead) इस तार पर फिसलती है। वृत्त को एक ऊर्ध्वाधर अक्ष AB के परितः चित्रानुसार कोणीय वेग ω से घुमाया जाता है तो वृत्त के सापेक्ष मणिका चित्रानुसार बिन्दु P पर स्थिर पायी जाती है। ω2 का मान होगा
View SolutionA bead can slide on a smooth circular wire frame of radius R which is fixed in a vartical plane. The bead is displaced slightly from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle theta made by the bead with the vertical line is
View Solution2pi r A frictionless wire of length is drawn in a circle and placed in a vertical plane. A bead slips on this wire. Angular velocity of the circle on a vertical axis AB: omega When rotated from, the manika is found to be stationary at the point P as per the picture, relative to the circle. omega^(2) Value of
View SolutionA bead can slide on a smooth circular wire frame of radius r which is fixed in a vertical plane. The bead is displaced slighty from the highest point of the wire frame. The speed of the bead subsequently as a function of the angle theta made by the bead with the verticle line is
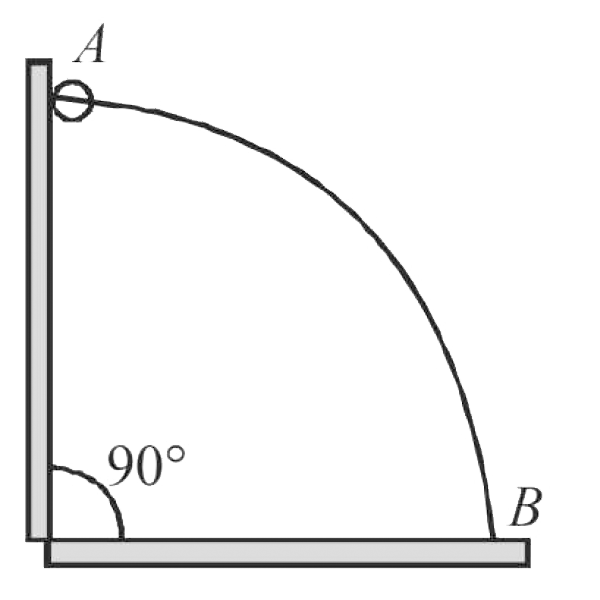
View SolutionA wire, which passes through the hole in a small bead, is bent in the form of quarter of a circle. The wire is fixed vertically on ground as shown in the figure. The bead is released from near the top of the wire and it slides along the wire without friction. As the bead moves from A to B, the force it applies on the wire is
View SolutionA small bead of mass 'm' is threaded on a frictionless circulat wire of radius 'a' . The circule wire frame is rotated about its vertical diameter as shown. (assume acceleration due to grasvity is g) The angular speed required if the bead is to be made to move in a horizontal circle of radius (a sqrt(3))/(2) is :
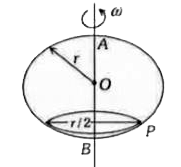
View SolutionA smooth wire is bent into a vertical circle of radius a. A bead P can slide smoothly on the wire. The circle is rotated about vertical diameter AB as axis with a speed omega as shown in figure. The bead P is ar rest w.r.t. the circular ring in the position shown. then ω2 is equal to:

View SolutionA small ring P is threaded on a smooth wire bent in the form of a circle of radius a and centre O. The wire is rotating with constant angular speed omega about a vertical diameter xy, while the ring remains at rest relative to the wire at a distance (a)/(2) from xy. Then omega^2 is equal to:
View Solution